Модель структурной схемы

Если систему представить тремя указанными выше моделями, то мы будем иметь представление о том:

• что поступает в систему из внешней среды и что система передает во внешнюю среду;

• из каких частей и элементов состоит система;

• как части системы между собой связаны.

Существует и четвертая модель, которая объединяет три рассмотренные модели, носит название «структурная схема» и изображена на рис. 4.4.

Рис. 4.4. Модель структурной схемы

Подобную модель еще называют «белым, или прозрачным, ящиком» как противоположность модели «черного ящика», которая не дает информации о содержании системы и ее внутренних связях.

Таким образом, можно сформулировать второе определение системы. Система есть совокупность взаимосвязанных элементов, обособленная от среды и взаимодействующая с ней как нечто целое.

Анализ моделей структурной схемы различных систем привел математиков к выводу о том, что общим для всех структурных схем является наличие элементов и связей между ними. В результате получилась схема, в которой обозначается только наличие элементов и связей между ними, а также разница между элементами и связями. Такая схема называется графом.

В теории систем управления используются графы, имеющие линейную (а), древовидную (б), матричную (в) и сетевую (г) структуру (рис. 4.5).

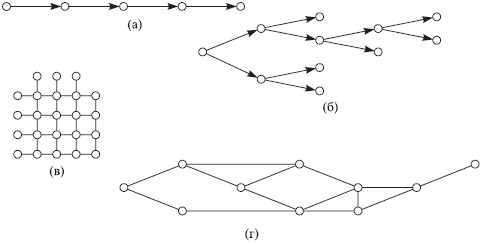
Рис. 4.5. Графы, соответствующие различным структурам

В линейной структуре между элементами системы устанавливается линейная (последовательная) связь.

В иерархической (древовидной) структуре, напоминающей дерево, перевернутое корнем вверх, отражаются связи, определяющие соподчиненность элементов, их иерархию. В теории организации иерархия определяет принципы эффективного функционирования различных видов систем. Иерархические структуры являются декомпозицией системы в пространстве. В теории иерархических структур выделяют особые классы многоуровневых иерархий. Они называются стратами, слоями или эшелонами. Такие иерархии обладают различными принципами взаимоотношений элементов в пределах уровня и приоритетом вмешательства высшего во взаимоотношения элементов нижележащего уровня.

Матричная структура не имеет иерархической направленности, а представляет собой в общем виде связи между элементами в виде сочетания строк и столбцов.

Сетевая структура есть представление (декомпозиция) сложной структуры во времени. Она включает вершины, пути и ребра. Сетевые элементы могут располагаться параллельно и последовательно. Они чаще всего бывают однонаправленными.

[1] Аналогия – подобие, сходство предметов в каких‑либо свойствах, признаках, отношениях.

Дата добавления: 2014-01-04