Сила притяжения якоря и магнитная проводимость воздушного зазора

Схема замещения магнитных цепей.

При замещении магнитных цепей электрической кривой ее участок замещения эквивалентным магнитным сопротивлением, а магнитодвижущая сила изображается как источник потока. Для упрощения расчетов принимают всю длину сердечника за один участок, а поток рассеяния (утечка) считают соссредомагнитным в его середине (используется приведенное сопротивление рассеяния). При таких упрощениях схема ЭММ и его электрическая схема замещения имеют вид, показанный на рисунке 5.5.

Рис 5.5- схема замещения ЭММ типа- 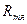-магнитное сопротивление якоря; 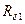,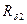-воздушных зазоров (рабочего и нерабочего); 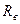,-верхних частей якоря и ярма; ,-нижней части якоря и ярма;

-основание; 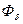-рабочий поток; Ф -конечный поток; 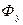-поток утечки; 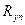-приведенное сопротивление утечки.

Если магнитопровод ненасыщен то,

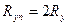
где 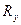-полное сопротивление утечки (рассеяния).

Если магнитопровод насыщен (для стопы В=1.1…1,2Тл), то

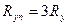
Для расчетов вводится конечный коэффициент рассеяния- отношение максимального потока Ф к потоку в рабочем воздушном зазоре :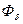

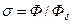(5.10)

Т.к. 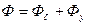, то (5.11)

Точные выражения для силы и момента 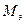, действующих на якорь магнита имеют вид:

;

Где 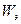полная электромагнитная энергия; х и 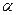- линейное и угловое перемещение якоря.

Для упрощения расчетов учитывают лишь энергию, сосредоточенную в рабочих воздушных зазорах. С учетом этого, например, для ЭММ сплошного тела, у которого сердечника более чем в 2 раза превышает длину основания и для ЭММ с движущимся якорем имеем:

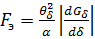, (5.12)

где 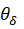- падение магнитной силы обмотки на рабочем воздушном зазоре (ФδRδ); 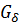– магнитная проводимость рабочего воздушного зазора

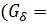1/Rδ).

ЭММ, у которых при изменении δ проводимость рассеивания Gy переменна (ЭММ сплошного типа, у которых длина основания больше длины сердечника или ЭММ типа) имеем:

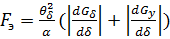, (5.13)

Выражение (5.13) для ЭММ сложного типа имеет вид:

(5.14)

где z – длина части сердечника, находящегося в катушке; lk – длина всей катушки; g – удельная проводимость потоков рассеивания:

g = Gy/l

где l – радиус длины поверхности рассеивания

Выражение для Fэ токов ЭММ приводится в литературе

Формула для Mэ отличается от 5.12 – 5.14 только заменой:

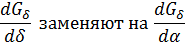
Если принять распределение Фδ в рабочем воздушном зазоре равномерным и пренебречь потоками, то можно воспользоваться формулой Максвелла:

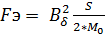, (5.15)

где S – полуось полюса.

Этой формулой пользуются при d/δ >5 (для цилиндрического сечения зазор диаметром d); при a/δ >5 и b/δ > 5 (для прямоугольного сечения зазора длиной a и шириной b). При этом погрешность расчета менее 20%. Так же данной формулой пользуются для определения Fэ при полностью притянутом якоре (при этом ).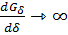

Для расчета магнитных цепей необходимо знать магнитные сопротивления (проводимости) и их производных воздушных зазоров различных форм.

При малых воздушных зазорах, когда отношения характерного размера сечения (a, b, d или t) к δ больше 5 согласно (5.5) имеем:

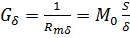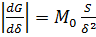; (5.16)

где S – площадь полюсов.

Если условия полости зазора не выполняются, то используется метод, согласно которому пространство воздушного зазора разбивается на элементарные объемы так, чтобы магнитные потоки, пронизывающие эти объемы, были параллельны друг другу. Зная проводимости этих элементарных объемов, общую проводимость воздушного зазора объединяют их суммированием. Выражения для проводимости элементарных воздушных объемов приводятся в специализированной литературе(Элементы приборных устройств: Курсовое проектирование. Учебное пособие для вузов. В 2-x ч Ч.1 Расчеты/ Под ред. О.Ф.Тименко. – М.:Высш.школа, 1978. – 328 с на стр. 280 – 282).

Дата добавления: 2014-01-04