Условиях I-рода

Однородную, однослойную стенку при граничных

Теплопроводность через цилиндрическую

Через цилиндрическую стенку

Перенос теплоты

Ось OZ совмещаем с осью цилиндра, и температура меняется только вдоль радиуса цилиндра.

Для полого цилиндра заданы: внешний () и внутренний (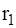) радиусы, коэффициент теплопроводности (l), температуры холодной и горячей стенок (и ).

Требуется найти: уравнение, описывающее температурное поле в цилиндре, т.е. изменение температуры в зависимости от диаметра d (радиуса r), а также плотность теплового потока q и сам тепловой поток Q.

На основании дифференциального уравнения теплопроводности при стационарном режиме и отсутствии внутренних источников теплоты (2.10), учитывая, что первая и вторая производные температуры по z равны нулю

, ,

а также то, что температура не зависит от полярного угла j, то уравнение Лапласа в цилиндрических координатах (2.10) упрощается до вида

. (4.1)

Граничные условия дифференциального уравнения:

при ;

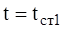при .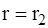

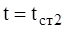Введём новую переменную

,

тогда дифференциальное уравнение (4.1) будет иметь вид:

.

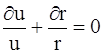Интегрируем данное выражение:

.

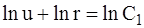Тогда, потенциируя это выражение и переходя к первоначальным переменным мы получаем:

.

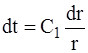После интегрирования получаем:

. (4.2)

Для определения постоянных интегрирования и воспользуемся граничными условиями:

(а)

Решая уравнение (а) относительно и , получаем

, (б)

, (с)

Подставляя в (4.2) значения и , получаем окончательное решение дифференциального уравнения

. (4.3)

Это решение описывает распределение температуры в цилиндрической стенке. Это логарифмическая кривая (рис. 4.1). Задавая произвольным диаметр, можно определить температуру в любой точке цилиндрической поверхности.

Согласно закону Фурье плотность теплового потока пропорциональна градиенту температуры (температура меняется только вдоль радиуса):

;

, Вт. (4.4)

Из этого выражения следует, что тепловой поток полностью определяется внутренним и наружным диаметрами цилиндра (и ).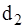

Тепловой поток может быть отнесён к единице длины цилиндра

, . (4.5)

(линейная плотность теплового потока) – это количество теплоты, проходящее через цилиндрическую поверхность путём теплопроводности через единицу длины

Тепловой поток может быть отнесён к внутренней поверхности цилиндра

, . (4.6)

Тепловой поток, отнесённый к наружной поверхности цилиндра

, . (4.7)

Связь между различными приведёнными плотностями теплового потока следующая

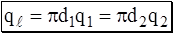, (4.8)

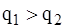, т.к. .

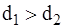Следовательно, в отличие от плоской стенки плотность теплового потока непостоянна по толщине цилиндрической стенки и определяется текущим диаметром цилиндра (чем больше текущий диаметр, тем меньше плотность теплового потока).

Если коэффициент теплопроводности не является величиной постоянной, а зависит от температуры по зависимости 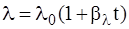, то температурное поле, т.е. линии изменения температуры в цилиндрической стенке, на любом диаметре может быть определено из следующего выражения

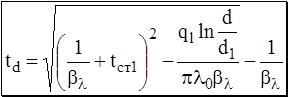. (4.9)

Подставляемые в выражение (4.9) значения 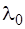и берутся из справочников.

Дата добавления: 2014-01-04