Сохранение ширины ленты матрицы в QR-, QL-алгоритмах

Ускорение сходимости QR-, QL-алгоритмов. Сдвиг по отношению Рэллея, по Уилкинсону.

Два представления о сходимости QR-, QL-алгоритмов

QR-, QL-алгоритмы решения полной проблемы собственных значений

План

Лекция 26. Алгоритмы решения полной проблемы собственных значений

Питання

1. Визначеня частинною похідною функції.

2. Яку поведінку функції багатьох змінних описує частинна похідна?

3. Як повязане існування похідної функції багатьох змінних в точці з існуванням частинних похідних функції в цій точці?

4. Чим є частинні похідні в точці функції для її повної похідної?

5. Що можна сказати про диференційованість функції у поданій точці, якщо в цій точці вона має всі частинні похідні?

6. Що означає, що?

7. Достатня умова диференційованості функції багатьох змінних.

8. Визначення похідної функції в точці за напрямом.

9. Як повязані між собою диференційованість функції в точці і існуванні в цій точці похідних за різними напрямами?

10. Вирази для обчислення похідної за напрямом.

11. Визначення градієнту функції.

1. QR-, QL-алгоритмы решения полной проблемы собственных значений

QR-, QL-алгоритмы решения полной проблемы собственных значений наиболее эффективны для небольших матриц (размера 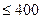). Эти алгоритмы эффективны для симметричных ленточных матриц, особенно для трехдиагональных.

Основная идея: QR-, QL-алгоритмы за счет подобных преобразований быстро уменьшают внедиагональные элементы, пока они не станут пренебрежимо малыми.

Любая ненулевая матрица 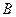може быть представлена в виде произведения:

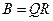(1)

где 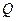- ортогональная вещественная матрица (т.е. 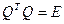, 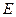- единичная матрица соответствующего размера), 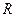- верхняя треугольная матрица с неотрицательными диагональными элементами. Матрицы 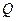и 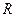определяются однозначно.

Если 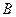- невырожденная вещественная матрица, то 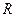- это верхний множитель Холесского для симметричной положительно определенной матрицы :

.

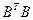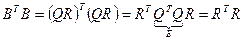Для матрицы 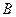возможно разложения вида:

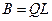(2)

где 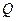- ортогональная вещественная матрица (т.е. 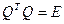, 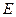- единичная матрица соответствующего размера), 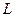- нижняя треугольная матрица. Эта матрица получается из соответствующего разложения матрицы 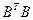с учетом :

.

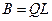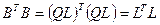Пример. Построить 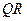, 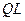- разложения матрицы

.

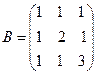Матрица 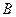является невырожденной, поэтому 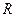- верхний множитель Холесского для матрицы 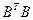. Вычислим элементы матрицы 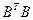и построим для нее разложение Холесского:

,

.

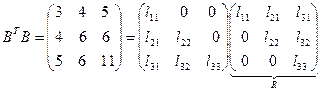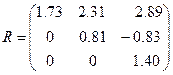Элементы матрицы 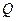определяются из матричного соотношения:

,

.

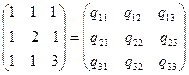
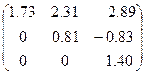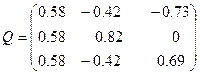Таким образом, 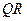- разложение исходной матрицы выглядит следующим образом:

.

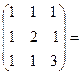
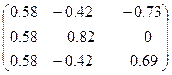
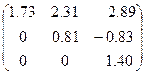Построим теперь для матрицы 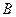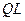- разложение. Для этого:

.

Составляя уравнения для элементов матрицы 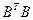в порядке, отмеченном выше, получим

.

.

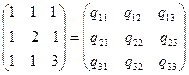
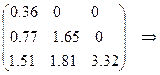
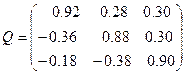Таким образом, 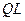- разложение исходной матрицы выглядит следующим образом:

.

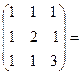
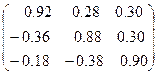
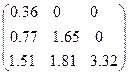Для определенности рассмотрим далее 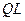-алгоритм.

Пусть дана матрица 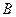и число 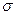, называемое сдвигом (сдвиг используется для ускорения сходимости 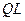-алгоритма). Для матрицы 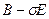построим 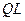-разложение:

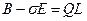. (3)

Из (3) выразим :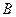

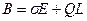. (4)

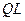-преобразование матрицы 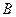с учетом (4) определим следующим образом:

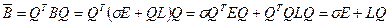. (5)

Поскольку 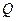- ортогональная матрица, это преобразование является подобным.

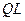-алгоритм.

Обозначим исходную матрицу 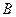через 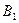. Для 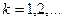делать

1. Определить сдвиг 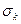, построить 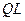-разложение матрицы :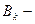

.

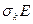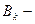
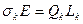2. Построить .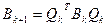

3. Проверка сходимости алгоритма.

Числа 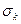выбираются так, чтобы ускорить сходимость 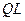-алгоритма. Каждый шаг алгоритма генерирует очередную матрицу 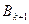, подобную исходной матрице .

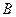Дата добавления: 2014-01-04