
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Карно
|
|
|
|
Эта теорема была доказана немецким термодинамиком Р. Клаузиусом (1822 – 1888) через полвека после публикации идей Карно в 1824 году. Результаты доказательства теоремы Карно для теплового двигателя были естественным путем перенесены на холодильный цикл Карно.
Теорема Карно содержит три результата:
1. Термический коэффициент полезного действия определяется выражением (4.6).
2. Термический коэффициент полезного действия не зависит от свойств рабочего тела.
3. Термический коэффициент полезного действия максимален среди всех других циклов в тех же температурных пределах.
Доказательство первого утверждения уже проведено в (4.6).
Доказательство второго состоит в следующем. Зададимся вопросом: «В каких параметрах состояния, в каких функциональных связях непосредственно проявляются теплофизические свойства конкретных, индивидуальных веществ?». Ответ на вопрос таков: изменение энтропии (см. лекцию 2) рассчитывается через среднюю массовую теплоемкость вещества, а она является характеристикой этого вещества. Далее, уравнения состояния, т.е. зависимость потенциала какого-то рода от всех координат состояния, индивидуально для каждого вещества в любой фазе. Это тоже носитель свойств вещества. Таким образом, изменение энтропии Δs в любом процессе сильно зависит от свойств вещества. Но в связи с тем, что величина Δs входит и в числитель и в знаменатель в выражении для ηtк, то эту величину можно сократить, и эта процедура строга математически. Отсюда и следует, что величина термического коэффициента полезного действия ηtк не зависит от свойств рабочего тела, носитель свойств Δs исчезла из выражения для ηtк.
Доказательство третьего утверждения получим из рассмотрения рис. 4.5.
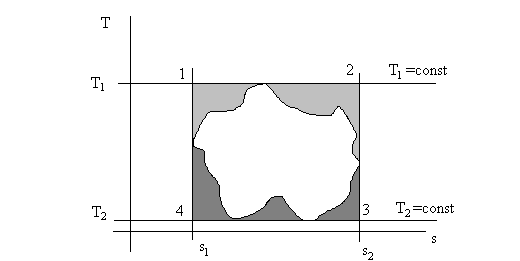
Рис. 4.5. Иллюстрация к доказательству максимальности
термического коэффициента полезного действия цикла Карно.
На рис. 4.5 показана диаграмма T – s, изображен цикл Карно и любой (произвольный) цикл в тех же температурных пределах Т1 и Т2. Вспомним, что
ηtк = 1 – q2 / q1,
где q1 – количество теплоты, полученной рабочим телом в источнике теплоты,
q2 – количество теплоты, отданной рабочим телом в холодильнике.
Глядя на рис. 4.5 видно, что q2 > q2к на величину заштрихованной справа налево площади под графиком. Здесь q2 – отданная теплота в холодильнике любого цикла, q2к – то же, но в цикле Карно. Аналогично, видно, что q1к > q1, поэтому в целом ηtк > ηt для любого цикла, вписанного в цикл Карно. Теорема Карно доказана.
Пример. Температура вспышки паров бензина в двигателе внутреннего сгорания (ДВС) равна примерно 20000С, а температура атмосферы летом 200С. Найти термический коэффициент полезного действия двигателя ДВС, работающего по циклу Карно.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 474; Нарушение авторских прав?; Мы поможем в написании вашей работы!