Pасчет простого трубопровода постоянного сечения

Классификация трубопроводов

ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ

Движение жидкости в трубопроводах происходит благодаря работе насосов за счет разности уровней или путем создания давления в емкости, из которой подается жидкость.

Простыми трубопроводами называются трубопроводы, не имеющие ответвлений и раз­ветвлений. Сложные трубопроводы имеют последовательно и параллельно соединенные участки.

Короткие трубопроводы - это трубопроводы, местные потери в которых составляют больше 5÷10% от суммарных потерь напора: h _м.с.> (5÷10)%Σ h _пот.

Длинные трубопроводы - местные потери в которых составляют меньше (5÷10)% от сум­марных потерь напора: h _м.с.< (5÷10%)Σ h _пот.

Суммарные nотери для длинных трубопроводов: h = (1,05÷1,1) λ (вводится поправка на местные потери).

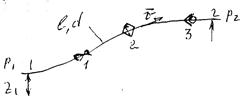
1 - вентиль; 2 - фильтр; 3 - обратный клапан

Уравнение Бернулли для сечений 1-1 и 2-2 потока реальной жидкости:

z ₁ + p ₁/ ρg + α v₁²/2 g = z ₂ + p ₂/ ρg + α v₂²/2 g + Σ h _пот.

Так как трубопровод постоянного диаметра, то v₁=v₂.

Запишем уравнение Бернулли в следующем виде:

p ₁/ ρg = ∆ z + p ₂/ ρg + Σ h _пот., где ∆ z = z ₂ – z ₁.

Введем обозначения:

p ₁/ ρg = Н _потр. - потребный напор для обеспечения необходимого расхода;

∆ z + p ₂/ ρg = Н _ст - статический напор;

Σ h _пот.= КQ ^m.

Тогда Н _потр. = Н _ст+ КQ^m, где К - коэффициент сопротивления трубопровода.

Для ламинарного течения m = 1 - Σ h _пот. = КQ;

для турбулентного течения m = 2 - Σ h _пот. = КQ ².

Характеристикой трубопровода называется зависимость суммарных потерь от расхода: Σ h _пот = f (Q). Характеристика трубопровода может быть выражена в аналитическом, графиче­ском или табличном виде.

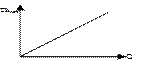
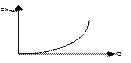
Рис. Характеристики трубопроводов

а) для ламинарного течения б) для турбулентного течения

1. Докажем, что для турбулентного течения m = 2, т.е. Σ h _пот = КQ ²:

Σ h _пот = h _тр.+ h _м.с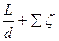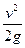. = (λ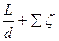)= 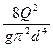(λ)= (λ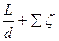) = КQ ²,

где К = 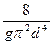(λ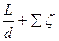), т.е. m = 2.

2. Докажем, что для ламинарного течения m = 1, т.е. Σ h _пот = КQ.

Для ламинарного течения при замене местных сопротивлений эквивалентными длинами, когда L _расч = L + Σ L _экв., или для длинных трубопроводов, когда L _расч.=(1,05÷1,1) L:

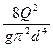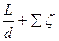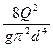Σ h _пот =(λ) = λ = = =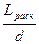

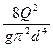
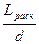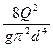
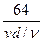
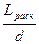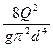
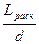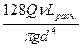= = = КQ, т.е. m = 1.

Покажем зависимость потребных напоров от расхода жидкости Н _потр. = f (Q) (кривые по­требного напора).

Для ламинарного течения Для турбулентного течения

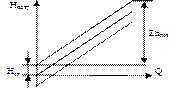
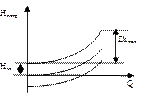
Рис. Кривые потребного напора

Статический напор Н _cт. положителен, если жидкость поднимается вверх или движется в по­лость с повышенным давлением.

Статический напор Н _ст отрицателен, если жидкость опускается вниз или движется в по­лость с разрежением.

Дата добавления: 2014-01-04