Режимы движения жидкости. Число Рейнольдса

В зависимости от рода жидкости, скорости ее движения и характера стенок, ограничивающих поток, различают два основных режима движения: ламинарный и турбулентный. Ламинарным называют упорядоченное движение, когда отдельные слои скользят друг по другу, не перемешиваясь (рис. 26, а).

Ламинарный режим движения можно наблюдать чаще у вязких жидкостей, таких как нефть, масла и т. п.

Турбулентным называют режим, при котором наблюдается беспорядочное движение, когда частицы жидкости движутся по сложным траекториям и слои жидкости постоянно перемешиваются друг с другом (рис. 26, б).

Существование двух режимов движения жидкости было замечено в 1839 г. Хагеном и в 1880 г. Д. И. Менделеевым.

Достаточно полные лабораторные исследования режимов движения и вопрос их влияния на характер зависимости потерь напора от скорости впервые исследовал английский физик Рейнольдс.

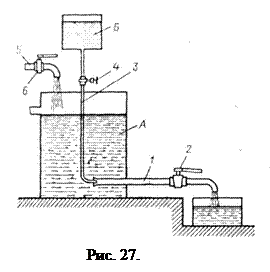
Установка Рейнольдса для исследования режимов движения жидкости пред ста влена на рис. 27. Сосуд А заполняется испытуемой жидкостью. К сосуду А в нижней его части присоединена стеклянная трубка 1 с краном 2, которым регулируется скорость течения в трубке. Над сосудом А расположен сосуд Б с раствором краски. От сосуда Б отходит трубка 3 с краном 4. Конец трубки 3 заведен в стеклянную трубку 1. Для пополнения сосуда А служив трубка 5 с запорным устройством 6.

При ламинарном режиме движения жидкости по трубке 1 струйка раствора краски, истекающей из трубки 3, имеет вид четко вытянутой нити вдоль трубки 1.

По мере открытия крана 2 увеличивается скорость движения и режим движения переходит в турбулентный, при этом струйка приобретает волнообразный характер, а при еще большей скорости совсем размывается и смешивается с жидкостью в трубке. При постепенном закрытии крана эти явления протекают в обратном порядке, т. е. турбулентный режим сменяется ламинарным.

Опыты показали, что переход от турбулентного режима к ламинарному происходит при определенной скорости (эта скорость называется критической), которая различна для разных жидкостей и диаметров труб; при этом критическая скорость растет с увеличением вязкости жидкости и с уменьшением диаметра труб.

Рейнольдсом и рядом других ученых опытным путем было установлено, что признаком режима движения является некоторое безразмерное число, учитывающее основные характеристики потока

, (82)

где – скорость, м/сек; R - гидравлический радиус, м; v - кинематический коэффициент вязкости, м²/сек.

Это отношение называется числом Рейнолъдса. Значение числа R_e, при котором турбулентный режим переходит в ламинарный, называют критическим числом Рейнолъдса R_eKp.

Если фактическое значение числа R_e, вычисленного по формуле (82), будет больше критического R_e > R_eKp – режим движения турбулентный, когда R_e < R_eKp – режим ламинарный.

Для напорного движения в цилиндрических трубах удобнее число Рейнольдса определять по отношению к диаметру d, т. е.

, (82')

где d – диаметр трубы.

В этом случае R_eKp получается равным ~2300. Если в формуле (82') для трубопроводов круглого сечения d выразить через гидравлический радиус , то получим R_eKp= 575. Для других трубопроводов и каналов некруглых сечений можно принимать значение критического числа Рейнольдса R_eKp =300 (при вычислении R_e через гидравлический радиус).

Дата добавления: 2014-01-04