Истечение жидкости через отверстия в тонкой стенке при постоянном уровне

Классификация отверстий и их практическое применение

НАСАДКИ

ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ,

Вопрос истечения жидкости через отверстия является одним из узловых моментов гидравлики. Ученые и инженеры изучали этот вопрос начиная с XVII в. Уравнение Д. Бернулли впервые было выведено при решении одной из задач на истечение жидкости из отверстия. При расчетах диафрагм, дырчатых смесителей, наполнении и опорожнении резервуаров, бассейнов, водохранилищ, шлюзовых камер и других емкостей решаются задачи на истечение жидкостей через отверстия. При решении этих задач определяют скорости и расходы жидкостей.

Экспериментально установлено, что при истечении жидкости из отверстий происходит сжатие струи, т. е. уменьшение ее поперечного сечения. Форма сжатой струи зависит от формы и размеров отверстия, толщины стенок, а также от расположения отверстия относительно свободной поверхности, стенок и дна сосуда, из которого вытекает жидкость. Сжатие струи происходит вследствие того, что частицы жидкости подходят к отверстию с разных сторон и по инерции движутся в отверстии по сходящимся траекториям.

Параллельное течение струй в отверстии возможно только в том случае, когда толщина стенок сосуда близка к размерам отверстия, а стенки отверстия имеют плавные очертания, с расширением внутрь сосуда. При этом отверстие превращается в коноидальный осадок (см. ниже).

Отверстия классифицируют следующим образом:

1.По размеру.

а) малые отверстия, когда или (рис. 38), где 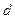– диаметр круглого отверстия; – напор; 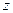– разность напоров при затопленном отверстии;

б) большие отверстия, когда или .

2. По толщине стенки, в которой сделано отверстие:

а) отверстия в тонкой стенке, когда 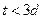или , где t – толщина стенки;

б) отверстия в толстой стенке, когда или .

3.Поформеразличают круглые, квадратные, прямоугольные, треугольные и другие отверстия.

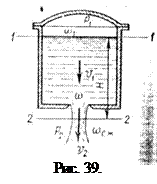Выведем формулы скорости и расхода жидкости при истечении через малое отверстие. Пусть жидкость вытекает из большого резервуара через малое отверстие в его дне или стенке (рис. 39).

Опытами установлено, что сжатое сечение струи находится от внутренней поверхности резервуара на расстоянии около половины диаметра отверстия. Эта величина обычно бывает мала сравнительно с напором Н в резервуаре, и можно считать, что центр отверстия и центр сжатого сечения струи находятся на одинаковой высоте, тем более при отверстии в боковой стенке.

Высоту уровня жидкости в резервуаре Н над центром отверстия называют геометрическим напором. В общем случае давление в резервуаре отличается от давления в пространстве, куда истекает жидкость.

Проведем плоскость сравнения 2-2 через центр сжатого сечения струи.

Уравнение Д. Бернулли применить к сечению отверстия нельзя, так как струйки в последнем сходятся под большими углами, и движение жидкости в нем не плавно изменяющееся.

Напишем уравнение Д. Бернулли для сечений 1-1 и 2-2

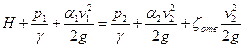, (124)

где – скорость подхода жидкости к отверстию в резервуаре; – средняя скорость течения в сжатом сечении; – коэффициент местного сопротивления при истечении через отверстие.

Перенесем наружное давление в левую часть и обозначим величину

. (125)

Эта величина называется напором истечения.

В правой части уравнения (124) вынесем за скобки . Тогда уравнение Д. Бернулли сведется к

,

откуда

.

Обозначим величину

. (126)

Величину называют коэффициентом скорости.

С учетом введенного обозначения

. (127)

Так как коэффициент Кориолиса , а коэффициент местных потерь напора в отверстии , то . По опытным данным , а . Отсюда

.

Для идеальной жидкост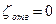и и 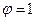. Тогда

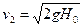. (128)

Это уравнение называется формулой Торичелли. Оно показывает, что скорость в начале вытекающей струи равна скорости свободного падения тела, упавшего с высоты .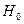

Когда поперечное сечение резервуара много больше площади живого сечения отверстия, а скорость жидкости в резервуаре незначительна (к примеру, меньше 0,1 м/сек), то скоростным напором 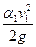можно пренебречь. В случае, когда давления снаружи и в резервуаре одинаковы 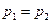, то весь напор истечения сводится к геометрическому напору, т. е. . Это бывает обычно при расчете истечения из открытых резервуаров в атмосферу.

Расход жидкости определится как произведение скорости истечения на площадь сжатого сечения струи

, (129)

где – коэффициент сжатия струи, равный отношению площади сжатого сечения к площади отверстия .

Величину 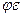обозначают через 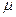и называют коэффициентом расхода.

Таким образом, расход жидкости, вытекающей через отверстие, определяют по формуле

. (130)

При точных измерениях размеров сжатого сечения струи установлено, что при совершенном сжатии струи . В этом случае . В общем же случае коэффициент расхода зависит от условий сжатия.

При истечении не в газовую среду, а в смежный резервуар с той же жидкостью (что принято называть истечением «под уровень»), т. е. когда отверстие затоплено с обеих сторон, в качестве геометрического напора Н принимают разность уровней жидкости в резервуарах. Числовые значения коэффициентов , и 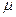остаются при этом практически теми же.

В случае круглого отверстия, расположенного на значительном расстоянии от стенок, струя сжимается со всех сторон одинаково, и в сжатом сечении имеет также форму круга; при этом сжатое сечение находится от кромок отверстия на расстоянии около половины диаметра отверстия – 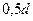. Величина коэффициента сжатия зависит от относительных размеров отверстия и от положения его относительно стенок резервуара и поверхности жидкости.

В зависимости от расположения отверстия различают следующие виды сжатия (рис. 40):

1) полное сжатие со всех сторон (отверстия 1 и 2);

2) неполное, когда сжатия нет с одной или нескольких сторон (отверстия 3, 4 и 5).

Полное сжатие подразделяют на:

а) совершенное, когда и (отверстие 1);

б) несовершенное, когда и 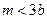(отверстие 2).

Форма сечения струи жидкости при истечении претерпевает изменения.

Эти изменения называются инверсией. Инверсия происходит вследствие того, что скорости подхода к отверстию в разных точках его периметра различны и вследствие сил поверхностного натяжения. На рис. 41 показано изменение формы струи при истечении через квадратное отверстие по мере удаления от резервуара.

При несовершенном сжатии коэффициент расхода вычисляют по формулам:

для круглых отверстий

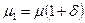(131)

для прямоугольных отверстий

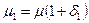(132)

где 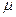– значение коэффициента расхода при совершенном сжати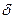и; и – поправочные коэффициенты, зависящие от отношения площади сечения отверстий к площади сечения сосуда . Значения этих коэффициентов принимают по таблице:

Значение величин 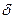и при несовершенном сжатии

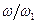
	0,10	0,20	0,30	0,40	0,50	0,60	0,70	0,80	0,90	1,00
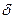
	0,014	0,034	0,059	0,092	0,134	0,189	0,26	0,351	0,471	0,631
	0,019	0,042	0,071	0,107	0,152	0,208	0,278	0,365	0,473	0,608

При неполном сжатии коэффициент расхода вычисляют по уравнениям:

для круглых отверстий

; (133)

для прямоугольных отверстий

, (134)

где 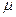– коэффициент расхода при полном сжатии; – часть периметра, на котором нет сжатия; Р – полный периметр отверстия.

При расчете больших отверстий значения коэффициентов расхода, рекомендованных Н. Н. Павловским, приведены в таблице:

Значения коэффициентов расхода для больших отверстий

Виды отверстий и характер сжатия струи	коэффициент расхода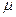
Большие отверстия с несовершенным, но всесторонним сжатием............................................................	0,70
Большие отверстия с умеренным боковым сжатием, без сжатия по дну..........................................................	0,80
Средние отверстия (шириной до 2 м) с весьма слабым боковым сжатием, без сжатия по дну ……….	0,90
Большие отверстия (шириной 5-6 м) с весьма слабым боковым сжатием, без сжатия по дну …………	0,95

Дата добавления: 2014-01-04