Связь реальной и пиковой производительности

Рассмотрим работу параллельной вычислительной системы, состоящей из n вычислительных модулей.

Под вычислительным модулем будем понимать любые устройства: например, ядра в мультипроцессорной системе, вычислительные узлы в кластерах, процессорные элементы в матричных системах типа SIMD; функциональные устройства (арифметико-логические устройства – АЛУ) в процессоре.

Пусть рассматриваемая параллельная вычислительная система выполняет программу. Практически в любой программе для параллельных систем можно выделить 2 части – последовательную и параллельную.

В последовательной части программы необходимо выполнить действия, которые невозможно распараллелить, например, инициация программы, ввод данных, вывод результатов, обмен данными между вычислительными модулями, часть действий, обусловленных сугубо последовательной природой алгоритма и т.п.

В параллельной части программы одновременно работают все задействованные по алгоритму вычислительные модули.

Примем, что производительность всех вычислительных модулей одинакова. Будем считать также, что последовательная часть программы выполняется на первом вычислительном модуле, а все остальные n-1 вычислительные модули при этом простаивают.

Будем считать, что вычислительные модули простые. Это означает, что новую операцию вычислительный модуль начинает только после завершения предыдущей операции.

Под операцией будем понимать любые действия, например, очередная команда программы типа «сложить два операнда и результат занести в регистр», процедура, некоторый алгоритм и т.л.

Пиковой производительностью будем называть максимальное количество операций, которое может быть выполнено вычислительной системой за единицу времени при полной загрузке всех вычислительных модулей.

Очевидно, что пиковая производительность характеризует потенциальную производительность параллельной вычислительной системы.

Аналогично определению пиковой производительности системы определим реальную производительность системы как сумму реальных производительностей задействованных при выполнении программы вычислительных модулей.

Интуитивно очевидно, что реальная производительность меньше его пиковой производительности, так как при выполнении реальных программ практически не удается полностью загрузить имеющиеся в параллельной системе вычислительные модули. Определим загруженность (коэффициент использования) вычислительного модуля как отношение объема реально выполненной работы за время Т к максимально возможному объему работы, которую вычислительный модуль может выполнить за тоже время Т.

Реальная производительность отдельно взятого вычислительного модуля будет равна произведению его пиковой производительности на его коэффициент использования (загруженность).

Реальная производительность параллельной вычислительной системы всегда будет меньше пиковой производительности. Отсюда видно, что для достижения наибольшей реальной про­изводительности каждого вычислительного модуля нужно обеспечить наибольшую его загру­женность. Для практических целей понятие производительности наиболее важно потому, что именно оно показывает, насколько эффективно вычислительный модуль выполняет полезную работу. По отношению к производительности понятие загруженности является вспомогательным. Тем не менее, оно полезно в силу того, что указывает путь повышения производительности, причем, через вполне определенные действия.

Хотелось бы и для системы вычислительных модулей ввести понятие загруженности, иг­рающее аналогичную роль. Его можно определять по-разному. Например, как и для одного вычислительного модуля, можно было бы считать, что загруженность системы вычислительных модулей есть отношение объема реально выполненной работы за время Т к максимально возможному объему работы системы за тоже время Т. Такое определение вполне приемлемо и позволяет сделать ряд полезных выводов. Однако имеются и возражения. В этом определении медленные и быстрые вычислительные модули оказываются равноправными и если надо повысить загруженность системы, то не сразу видно за счет какого вычислительного модуля это лучше сделать.

Большое число вычислительных модулей, так же как и конвейерные вычислительные модули, используются тогда, когда возникает потребность решить задачу быстрее. Чтобы понять, на­сколько быстрее это удается сделать, нужно ввести понятие "ускорение". Как и в случае загруженности, оно может вводиться различными способами, многообразие которых зависит от того, что с чем и как сравнивается. Нередко ускорение определяется, например, как отношение времени решения задачи на одном универсальном процессоре к времени решения той же за­дачи на системе из n таких же процессоров. Очевидно, что в наилучшей ситуации ускорение может достигать n. Отношение ускорения к n называется эффективностью. Заметим, что подобное определение ускорения применимо только к вычислительным системам, состоящим из одинаковых устройств, и не распростра­няется на смешанные вычислительные системы. Понятие же "эффективность" в рассматри­ваемом случае просто совпадает с понятием загруженности. При введении понятия "ускорение" мы поступим иначе.

Пусть алгоритм реализуется за время Т на вычислительной системе из n вычислительных модулей, в общем случае простых или конвейерных и имеющих пиковые производительности Pi …. Pn.. Предположим, что 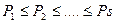. При реа­лизации алгоритма вычислительная система достигает реальной производительности Rc. Будем сравнивать скорость работы вычислительной системы со скоростью работы гипотетического простого универсального вычислительного модуля, имеющего такую же пи­ковую производительность Pn, как самый быстрый вычислительный модуль системы, и обладаю­щего возможностью выполнять те же операции, что все вычислительные модули системы.

Итак, будем называть отношение ускорением реализации алгоритма на данной вычислительной системе или просто ускорением. Выбор в качест­ве гипотетического простого, а не какого-нибудь другого, например, кон­вейерного вычислительного модуля объясняется тем, что один простой универсальный вычислительный модуль может быть полностью загружен на любом алгоритме.

(1)

Анализ определяющего ускорение выражения (1) показывает, что ускоре­ние системы, состоящей из n вычислительных модулей, никогда не превосходит n и может достигать n в том и только в том случае, когда все вычислительные модули системы име­ют одинаковые пиковые производительности и полностью загружены.

Подводя итог проведенным исследованиям, приведем для одного частного случая полезное, хотя и очевидное утверждение.

Если система состоит из n вычислительных модулей с одинаковой пиковой производительностью, то:

загруженность системы равна среднему арифметическому загруженностей всех вычислительных модулей;

реальная производительность системы равна сумме реальных производительностей всех вычислительных модулей;

пиковая производительность системы в n раз больше пиковой производительности одного вычислительного модуля;

ускорение системы равно сумме загруженностей всех вычислительных модулей.

Если система состоит только из простых вычислительных модулей, то ее ускорение равно отношению времени реализации алгоритма на одном универсальном простом вычислительном модуле с той же пиковой производительностью к времени реализации алгоритма на вычислительной системе.

Пусть система вычислительных модулей функционирует и показывает какую-то реальную производительность. Если производительность недостаточна, то в соответст­вии для ее повышения необходимо увеличить загруженность вычислительной системы. Для этого, в свою очередь, нужно повысить загруженность любого вычислительного модуля, у которого она еще не равна 1. Но остается открытым вопрос, всегда ли это можно сделать. Если вычислительный модуль загружен не полно­стью, то его загруженность заведомо можно повысить в том случае, когда данный вычислительный модуль не связан с другими из n вычислительных модулей. В случае же связанности вычислительных модулей ситуация не очевидна.

Не ограничивая общности, будем считать все вычислительные модули простыми, т. к. любой конвейерный вычислительный модуль всегда можно представить как линейную цепочку простых вычислительных модулей. Допустим, что между вычислительными модулями установлены направленные связи, и они не меняются в про­цессе функционирования вычислительной системы.

Тогда справедливо утверждение, что производительность вычислительной системы, состоящей из связанных между собой вычислительных модулей, в общем случае определяется самым непроизводительным вычислительным модулем.

Дата добавления: 2014-01-04