Алгоритм схемы простых процентов

А) алгоритм с применение годовой процентной ставки .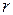

В формулу

подставим

получим

.

Решив последнее равенство относительно 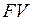, получим формулу наращения по схеме простых процентов с применением годовой ставки процентов:

. (1)

Разрешив формулу (1) относительно , получим формулу математического дисконтирования по схеме простых процентов:

. (2)

Проценты равны

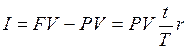. (3)

Замечание.

Формулу (3) можно записать в виде

,

где дивизор, 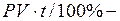процентное число.

В) алгоритм с применением годовой учетной ставки .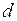

В формулу

подставим

и получим равенство

,

которое разрешим относительно 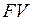и получим формулу наращения по схеме простых процентов с применением учетной ставки:

. (4)

Разрешив равенство (4) относительно , получим формулу дисконтирования по схеме простых процентов с применением процентной учетной ставки:

. (5)

В формулах (4) и (5) должно быть , что накладывает ограничение на период кредитования 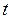при заданном значении учетной ставки 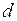, а именно:

. (6)

т. е. учётная ставка более жёстко отражает фактор времени.

Замечание.

1. Условимся в дальнейших формулах вместо писать просто 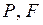. Например, формулу (1) теперь запишем в виде:

.

2. Расчеты по формуле (5) называют банковским дисконтированием (банковским учётом), поскольку они применяются банками при операции учёта векселей. Вексель – письменное безусловное обязательство векселедателя (заёмщика) уплатить в установленный срок определённую сумму предъявителю векселя или лицу, указанному в векселе.

3.3. Расчёт процентов при изменяющейся сумме вклада на счёте

На рис. 3 показан график изменения суммы вклада на счёте, где сумма вклада, хранящаяся неизменной в течение интервала времени .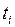

Если проценты за период 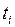не капитализируются, т. е. не присоединяются к сумме вклада, то согласно формуле (3) проценты за этот период равны

. (7)

Суммируя по всем периодам, получаем общую сумму процентов по вкладу:

. (8)

Полученный результат можно очевидным образом обобщить на произвольное число периодов срока хранения вклада на счёте.

Замечание.

Рассмотренный пример показывает, что в схеме простых процентов начисление процентов производится по периодам, в течение которых исходная сумма денежных средств не изменяется.

Дата добавления: 2014-01-04