Наращение с капитализацией (реинвестированием) процентов

Пусть срок ссуды разбит на периодов длительностью 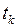, , 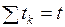и процентной ставкой в периоде .

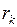В первом периоде наращенная сумма процентов составила

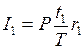
и эти проценты были присоединены к основной сумме 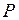. Таким образом, в следующем периоде наращение производится на сумму

.

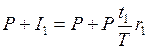
Это в конце второго периода даст сумму процентов

,

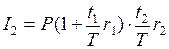а наращенная сумма за два периода будет равна

.

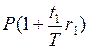
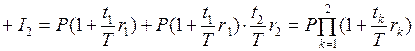Обобщая на все периодов, получим формулу наращения

. (12)

Важным является частный случай, когда все интервалы времени 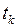равны, т. е. 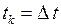, и равны процентные ставки: . Тогда формула (12) принимает вид:

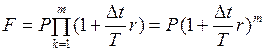. (13)

Замечание.

Формула (13) приводит нас к схеме сложных процентов.

3.6. Факторный учёт векселя

Рассмотрим диаграмму, которая наглядно показывает составляющие схему учёта банком векселя (рис. 4) Заёмщик решил взять кредит на сумму 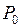на срок 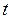по процентной ставке 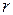. Им был выписан вексель на сумму 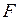к моменту погашению. Эта сумма была вычислена по схеме простых процентов:

.

По истечении некоторого времени 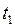владелец векселя принял решение учесть в банке (продать банку и получить наличными или положить на счёт для дальнейшего использования). Время до момента погашения векселя равно 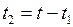выбирается им в соответствии с выполнением неравенства (6):

,

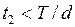где 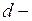учётная ставка, которую предложил банк владельцу векселя. На момент учёта векселя наращенная стоимость

.

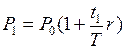Однако, банк, оказывая услугу по учёту векселя, желает получить комиссионные 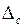и проценты , которые в сумме составляют дисконт (скидку) 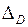с суммы 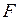. По этому на руки владелец векселя получит сумму

.

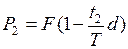При этом . Комиссионные за услугу составят

.

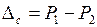Дата добавления: 2014-01-04