Дисконтирование по сложной процентной ставке

При решении задачи нахождения по заданному доходу 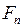текущей величины 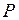при заданной доходности 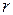и в общем случае при 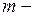кратном начислении применяют формулу:

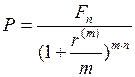. (44)

В этом случае дисконт составляет

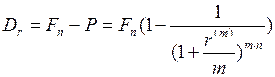. (45)

При смешанной схеме применяют формулу математического дисконтирования

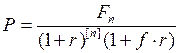. (46)

4.6. Сложная учётная ставка

В момент заключения финансовой сделки начисляются проценты (антисипативные проценты) на долговое обязательство 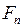со сроком погашения 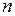лет.

Пусть оно досрочно учитывается с дисконтом по сложной учетной ставке 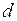. Так за год до срока погашения процент составит

,

а продавцу долгового обязательства будет причитаться сумма .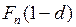

При учёте долгового обязательства за два года до погашения процент составит

,

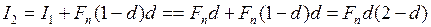продавцу будет причитаться сумма

.

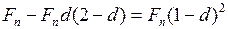Таким образом, сумма продавцу за 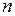лет до срока погашения долгового обязательства составит

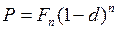, (47)

а дисконт равен

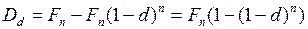. (48)

Таким образом, в момент оформления долгового обязательства на сумму 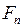будут учтены проценты в сумме 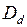(48) и продавец долгового обязательства получит сумму 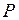(47).

Если 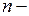нецелое число лет, то можно применить смешанную схему учёта:

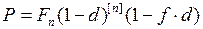. (49)

При дисконтировании раз в год по номинальной учётной ставке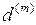

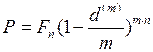. (50)

Если количество дисконтирования в году увеличивается, то

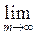
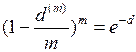. (51)

Если заданы 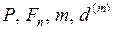, то срок до погашения долгового обязательства можно вычислить по формуле

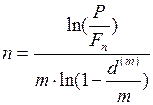. (52)

4.7. Эффективная учётная ставка

Так как возможны разные схемы дисконтирования сложных процентов, то знание номинальной учетной ставки не позволяет их сравнивать.

Определение. Учётная ставка, обеспечивающая переход от суммы 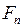к текущей сумме 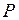при однократном дисконтировании процентов, называется эффективной и обозначается .

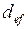Применение эффективной ставки должно обеспечивать равносильность схем наращения:

~ .

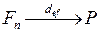Замечание. Чем выше учётная ставка, тем выше расходы заёмщика по обслуживанию полученной ссуды.

Из финансового эквивалента

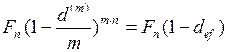(53)

находим размер эффективной учётной ставки

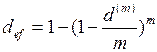. (54)

Обратный переход выполняется по формуле

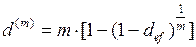. (55)

В контрактах со смешанным способом дисконтирования процентов по известным значениям 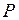и 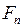находят эффективную учётную ставку

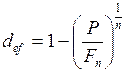. (56)

4.8. Наращение сложными процентами по учётной ставке

В общем случае формула наращения сложными процентами по учётной ставке имеет вид:

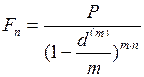. (57)

Сравнение наращений по процентной ставке с наращениями по учётной ставке даёт ответ: наращение по учётной ставке происходит более значительно.

Если в обязательстве применялись плавающие учётные ставки, то

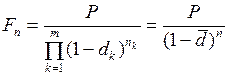, (58)

где 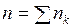, а средняя учётная ставка

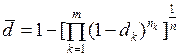. (59)

Дата добавления: 2014-01-04