Розділ 1. Вектори та координати

Розділ 8 Поверхні другого порядку 63

Розділ 7. Загальна теорія ліній другого порядку 58

Розділ 5. Лінії і поверхні 51

Розділ 4. Прямі і площини 36

Розділ 3. Перетворення систем координат 34

Розділ 2. Добутки векторів 18

Розділ 1. Вектори та координати 4

1.1. Напрямлені відрізки і їхня рівність.

Рис. 1.1. Рівність напрямлених відрізків.

1.2. Додавання напрямлених відрізків

.

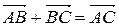Рис. 1.2. Додавання напрямлених відрізків і множення їх на числа

1.3. Добуток напрямлених відрізків на число. Нульовий напрямлений відрізок

.

Задача 1.1. Знайдіть вираз для напрямленого відрізку, що з'єднує будь-які дві точки на рисунку, у вигляді лінійної комбінації зазначених на рисунку відрізків і . Наприклад: .

Спробуйте одержати загальну формулу для довільного напрямленого відрізка:

.

Рис. 1.3. До задачі 1.1

1.4. Визначення вектора.

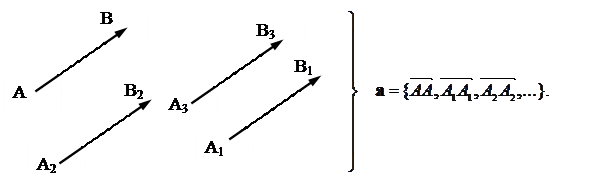
Рис. 1.4. Визначення вектора

1.5. Рівність векторів.

1.6. Довжина вектора.

1.7. Сума векторів.

Доказ_______________________________________________________________

Відповідно до властивості 1:

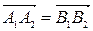(T1.1)

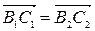
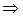
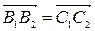. (Т1.2)

Із цих співвідношень маємо:

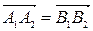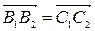
і (Т1.3)

Використовуючи ще раз властивість 1, дістаємо:

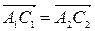. (Т1.4)

Рис. 1.5. До теореми 1

____________________________________________________________________

1.8. Множення вектора на число.

1.9. Напрямок вектора. Орт.

Вектор, який однонапрямлений даному векторові 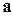і має одиничну довжину (позначають ), називають ортом і визначають таким чином:

.

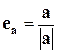Для нульових векторів, довжина яких дорівнює нулеві, орти не визначені.

Відповідно до визначення, орти мають одиничну довжину , і за допомогою його орта будь-який вектор можна записати у такому вигляді:

.

Задача 1.2.

Побудуйте вектор 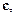напрямлений по бісектрисі кута, утвореного двома заданими векторами 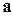і .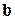

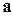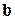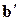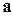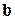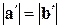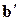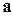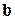Для розв’язку цієї задачі досить використати правило паралелограма, згадавши при цьому, що діагональ у паралелограмі є бісектрисою, якщо паралелограм є ромбом, тобто всі його сторони є рівними. Тому досить від векторів і перейти до векторів і , що напрямлені також, як і , відповідно, але мають однакові довжини . Як вектори і можна взяти орти векторів і : і . Тоді шуканий вираз для вектора 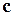буде виглядати в такий спосіб:

.

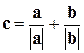Безумовно, можна запропонувати й іншій розв’язок цієї задачі, наприклад:

, і т. д. і т. п.

1.10. Властивості лінійних операцій над векторами.

.

Рис. 1.6. Сполучна властивість додавання векторів

1.11. Поняття лінійної залежності векторів.

.

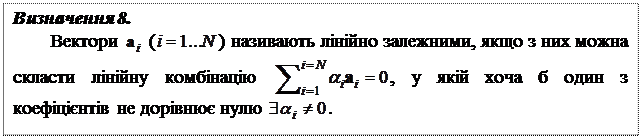
1.12. Розмірність простору. Базис простору.

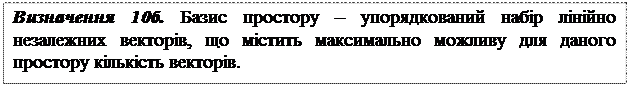
1.13. Координати вектора.

1.14 Проекція вектора. Ортогональні проекції.

1.15. Системи координат, радіус-вектор.

Сукупність початку відліку й базису називають системою координат. Вектор, який з’єднує початок відліку та певну точку, має спеціальну назву радіус-вектор цієї точки. Наприклад, радіус-вектор точки N позначають як

.

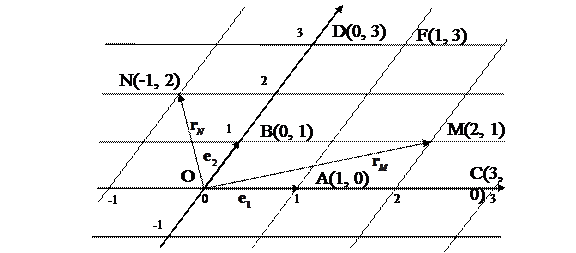
Рис. 1.7. Приклад системи координат

1.16. Декартові системи координат.

Розглянемо базиси, у яких базисні вектори перпендикулярні один одному й мають одиничну довжину. Наприклад, у двомірному випадку це базис

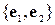, де і ;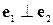

а в тривимірному випадку це базис

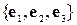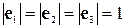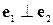, де і , і .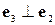

Такі системи називають декартовими системами координат, або ортонормованими системами координат. Декартові системи координат найчастіше застосовують розв’язуючи математичні й фізичні задачі, і тому координати в такій системі мають власні позначення – і найменування – абсциса, ордината й апліката відповідно.

Рис. 1.8. Декартова система координат на площині

1.17. Полярна система координат.

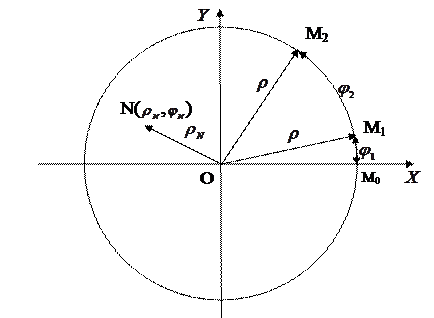
Рис. 1.9. Полярна система координат

Співвідношення між декартовими і полярними координатами:

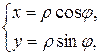
1.18.Циліндрична система координат

.

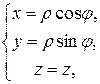
Рис. 1.10. Циліндрична система координат

1.19 Сферична система координат.

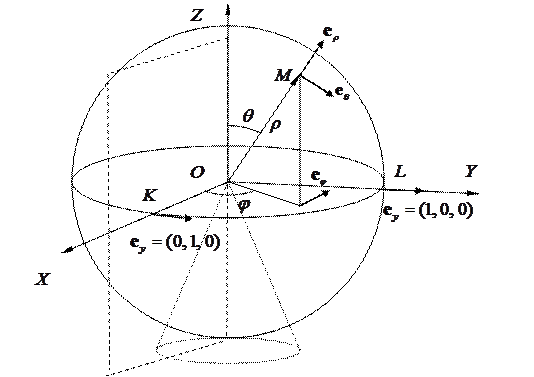
Рис. 1.11. Сферична система координат. Координатні поверхні й орти

1.20. Базиси й системи відліку різної орієнтації.

Рис. 1.12. Базиси різної орієнтації на прямій

Ортонормовані базиси однакової орієнтації можна сполучити рухами всередині простору, у якому їх визначено.

Рис. 1.13. Базиси різної орієнтації на площині

Рис. 1.14. Базиси різної орієнтації в просторі

Рис. 1.15. Визначення правого базису

Задача 1.3. Визначить вектор швидкості точки за рівномірного обертання.

Розв’язок. Припустимо, що точка обертається по колу з постійним радіусом і кутовою швидкістю ω. Радіус-вектор цієї точки дорівнює , а швидкість дорівнює похідній від радіуса-вектора за часом:

. (5.13)

В останньому перетворенні враховано, що радіус обертання не змінюється з часом. Орт залежить від положення точки, тому він змінюється з часом і похідна 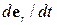не дорівнює нулеві. Щоб обчислити цю похідну, можна представити цей орт як лінійну комбінацію якихось векторів, що не змінюються з часом. Наприклад, можна представити у вигляді розкладання по базисних векторах декартового базису:

,

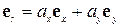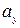де і – координати вектора у базисі :

, .

Кути, що входять у ці співвідношення виражаємо через кут φ між радіусом-вектором і віссю х (полярний кут у системі координат) й одержуємо, що

Тепер можна взяти похідну за часом від цього виразу:

.

Тут ми використали той факт, що похідна за часом від кута є кутовою швидкістю. Якщо тепер знайти вираз для орта 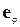у полярній системі відліку:

,

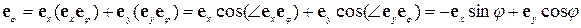то ми одержимо шуканий вираз для швидкості обертової точки:

.

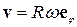Цей вираз визначає як величину лінійної швидкості обертання , так і напрямок , тобто швидкість спрямована по дотичній до окружності, по якій обертається точка.

Задача 1.4. Знайдіть відстань між точками в полярній системі координат.

Розв’язок. Нехай задано дві точк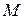и й у полярній системі координат через їх координати: 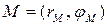і . Відстань між ними просто виразити через декартові координати:

.

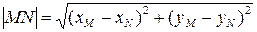Щоб використати цю формулу нам досить виразити декартові координати точок через полярні за допомогою співвідношень 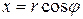і 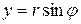. Підставлення цих виразів у формулу для довжини 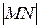дає:

.

Отримане співвідношення є ні що інше, як теорема косинусів, і наведений розв’язок можна розглядати як доказ теореми косинусів за допомогою координатного методу. У той же час це співвідношення можна переписати іншим способом, явно виділивши квадрат різниці довжин радіус векторів і доданок, що є малим, якщо є малим кут між радіусами-векторами

.

Такий вираз є особливо зручним у фізичних додатках, коли, наприклад, виникає необхідність розкладати величину 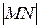у ряд Тейлора по малому параметру .

Більш того, одержаний вираз дозволяє знайти так званий «елемент довжини» у полярній системі відліку, або, іншими словами, відстань між двома нескінченно близькими точками:

.

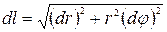Одержані співвідношення дозволяють вивести основні нерівності трикутника. Якщо врахувати, що величина 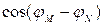лежить у межах від мінус одиниці до одиниці, то для величини 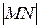одержимо:

.

Звідси випливають нерівності, що зв'язують між собою довжини сторін будь-якого трикутника:

.

Задача 1.5. Самостійно доведіть, що елемент довжини у сферичній системі координат дорівнює

.

Дата добавления: 2014-01-04