Виды средних и способы их вычисления

Рассмотрим теперь виды средних величин, особенности их исчисления и области применения.

Определить среднюю можно через исходное соотношение средней (ИСС) или ее логическую формулу:

Средние величины делятся на два больших класса: степенные средние, структурные средние.

К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.

В качестве структурных средних рассматриваются мода и медиана.

Остановимся на степенных средних. Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными. Простая средняя считается по не сгруппированным данным и имеет следующий общий вид:

,

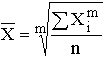где Xi – варианта (значение) осредняемого признака;

m – показатель степени средней;

n – число вариант.

Взвешенная средняя считается по сгруппированным данным и имеет общий вид

,

где Xi – варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;

m – показатель степени средней;

fi – частота, показывающая, сколько раз встречается i-e значение осредняемого признака.

Приведем в качестве примера расчет среднего возраста студентов в группе из 20 человек:

№ п/п	Возраст (лет)	№ п/п	Возраст (лет)	№ п/п	Возраст (лет)	№ п/п	Возраст (лет)
1 2 3 4 5	18 18 19 20 19	6 7 8 9 10	20 19 19 19 20	11 12 13 14 15	22 19 19 20 20	16 17 18 19 20	21 19 19 19 19

Средний возраст рассчитаем по формуле простой средней:

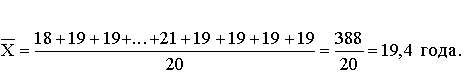
Сгруппируем исходные данные. Получим следующий ряд распределения:

Возраст, Х лет						Всего
Число студентов

В результате группировки получаем новый показатель – частоту, указывающую число студентов в возрасте Х лет. Следовательно, средний возраст студентов группы будет рассчитываться по формуле взвешенной средней:

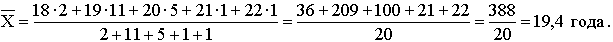
Общие формулы расчета степенных средних имеют показатель степени (m). В зависимости от того, какое значение он принимает, различают следующие виды степенных средних:

средняя гармоническая, если m = -1;

средняя геометрическая, если m –> 0;

средняя арифметическая, если m = 1;

средняя квадратическая, если m = 2;

средняя кубическая, если m = 3.

Формулы степенных средних приведены в табл. 4.4.

Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:

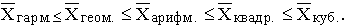
В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные.

Таблица 1

Виды степенных средних

Вид степенной средней	Показатель степени (m)	Формула расчета
Простая	Взвешенная
Гармоническая	-1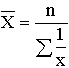
Геометрическая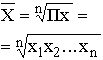
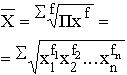
Арифметическая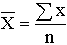
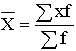
Квадратическая
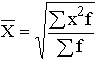
Кубическая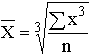

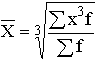
Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е. m = Xf). К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т.д.) предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали, изделия.

Главное требование к формуле расчета среднего значения заключается в том, чтобы все этапы расчета имели реальное содержательное обоснование; полученное среднее значение должно заменить индивидуальные значения признака у каждого объекта без нарушения связи индивидуальных и сводных показателей. Иначе говоря, средняя величина должна исчисляться так, чтобы при замене каждого индивидуального значения осредняемого показателя его средней величиной оставался без изменения некоторый итоговый сводный показатель, связанный тем или другим образом с осредняемым [1]. Этот итоговый показатель называется определяющим, поскольку характер его взаимосвязи с индивидуальными значениями определяет конкретную формулу расчета средней величины. Покажем это правило на примере средней геометрической.

Формула средней геометрической

используется чаще всего при расчете среднего значения по индивидуальным относительным величинам динамики.

Средняя геометрическая применяется, если задана последовательность цепных относительных величин динамики, указывающих, например, на рост объема производства по сравнению с уровнем предыдущего года: i1, i2, i3,..., in. Очевидно, что объем производства в последнем году определяется начальным его уровнем (q0) и последующим наращиванием по годам:

qn=q0× i1× i2×...×in.

Приняв qn в качестве определяющего показателя и заменяя индивидуальные значения показателей динамики средними, приходим к соотношению

Отсюда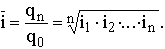

Дата добавления: 2014-01-04