Особые формы записи индекса цен

Индекс Паше (немецкий ученый-статистик):

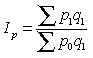. (9.16)

Индекс Ласпейреса (немецкий ученый-статистик):

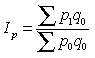. (9.17)

Индексируемой величиной обеих индексов являются цены.

Весами в индексе цен Паше выступает количество продукции текущего периода, а в индексе Ласпейреса — количество продукции базисного периода.

Как правило, значения индексов цен Паше и Ласпейреса не совпадают. Отличие значений объясняется тем, что индексы имеют различное экономическое содержание.

Индекс цен, исчисленный по формуле Паше, дает ответ на вопрос, насколько товары в текущий период стали дороже (дешевле), чем в базисный.

Индекс цен Ласпейреса показывает, во сколько бы раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетный период.

Индекс цен, рассчитанный по формуле Паше, имеет тенденцию некоторого занижения темпов инфляции, индекс Ласпейреса — завышения.

До начала 1990-х годов отечественная статистика отдавала предпочтение индексу цен Паше, а, начиная с 1991 г., на практике стал шире применятся индекс цен Ласпейреса, которому также отдается предпочтение и в мировой статистике.

Одним из важнейших показателей статистики цен, широко используемым в экономической и социальной политике, является индекс потребительских цен (ИПЦ). Он находит широкое использование при пересмотре социальных программ, служит основой для повышения минимального размера заработной платы, отражает реальную покупательную способность денег.

Методика расчета этого показателя включает следующие показатели.

Отбор товаров (услуг) — представителей и торговых предприятий, по которым регистрируются цены. Для вычисления ежемесячного ИПЦ отбор производится в соответствии с Общероссийским классификатором.

Индекс-дефлятор рассчитывается как отношение фактической стоимости продукции отчетного периода к стоимости объема продукции, структура которого аналогична структуре отчетного года, но определенного в ценах базисного года.

Итак, индексы — относительные показатели, предназначенные для описания изменения какой-либо величины во времени или в пространстве.

Или иначе, индекс — сводный, обобщенный итоговый показатель изменения изучаемого явления. По форме индексы подразделяются на индивидуальные, агрегатные и средние. Индивидуальные индексы дают меру изменения величины. Средние и агрегатные индексы дают картину изменения по составляющим индексируемой величины.

Индексы, рассчитанные цепным способом, называются цепными, рассчитанные базисным способом — базисными.

В индексах цен индексируются цены, а в качестве весов берутся натуральные количества произведенной продукции, а произведения дают стоимость отдельных видов продукции. Наиболее часто применяемые — это взвешенные агрегатные индексы типа ценовых. Рассмотрим еще основные приемы применения индексного анализа на примерах.

Пример 1. Реализация овощей на рынке характеризуется следующими показателями:

Наименование товара	Базисный период	Отчетный период
Кол-во	Цена за 1 кг, руб.	Кол-во	Цена за 1 кг, руб.
Картофель, т
Морковь, ц

Определим:

1) общий индекс физического объема продукции;

2) общий индекс цен;

3) абсолютный размер экономии или перерасхода денежных средств.

На основании вычисленных индексов (1 и 2) определим индекс товарооборота. Общий индекс физического объема исчисляется по формуле:

.

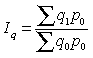Подставив значения параметров (количество в кг) в формулу, получим:

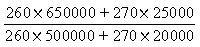
Следовательно, объем реализованной массы в неизменных ценах увеличился на 29,8%.

Общий индекс цен исчисляется по формуле:

.

Подставив значения параметров (количество в кг) в формулу, получим:

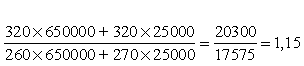
Следовательно, цены выросли в среднем на 15,5%.

Сравнив числитель и знаменатель индекса цен, получим абсолютный размер экономии или денежных средств:

= 20300 - 17575 = 2725.

Поскольку стоимость товаров в ценах базового периода ниже фактической, то потребители заплатили в отчетном периоде на 2725 руб. больше за счет роста цен, т.е. товарооборот в фактических ценах увеличился на 49,9%.

Покажем особенность применения средних индексов на следующем примере.

Пример 2. Имеются следующие данные о продаже товаров в розничной торговле области:

Группа товаров	Товарооборот, млн. руб.	Изменение количества проданных товаров, %
Базисный период	Отчетный период
Обувь			+15
Трикотажные изделия			+30

Для анализа объемов реализации определим:

1) общий индекс физического объема товарооборота;

2) общий индекс цен и абсолютный размер экономии (перерасхода) денежных средств.

Общий индекс физического объема товарооборота найдем по методу средних отношений базисных товарооборота к индивидуальным индексам количеств. Индивидуальные индексы количеств в нашем случае равны соответственно 1,15 и 1,3, поэтому:

.

Имеет место рост физического объема реализации на 22,2%. Общий индекс цен найдем аналогично по методу средних отношений, взвешивая на базисные товарооборота:

.

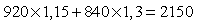Индекс показывает, что цены в среднем понизились на 13,5%.

Абсолютную величину экономии денежных средств определим как разность числителя и знаменателя:

Д = 1860 - 2150 = -290.

Знак «минус» означает, что имеется экономия: стоимость товаров в ценах базового периода выше фактической.

Различают также индексы постоянного и переменного состава.

Необходимость применения индексов постоянного и переменного состава возникает в том случае, когда динамика средних показателей отражает изменение не только усредняемого признака, но и состава данной совокупности.

Так, например, средняя цена на молоко может изменяться не только под влиянием изменения цены молока, но и в результате изменения структуры (состава) товарной массы; средняя себестоимость какого-либо изделия может измениться не только в результате изменения себестоимости этого изделия на заводах, но и в результате изменения удельных весов заводов с разной себестоимостью в общем выпуске этого изделия.

Этот индекс получил название индекса переменного состава, он отражает изменение усредняемого признака р и структуры совокупности (q t / S q).

Рассмотрим методику расчета индексов постоянного и переменного состава на примере индекса себестоимости продукции.

Пример 3. Имеются данные о выпуске одноименной продукции «А» и ее себестоимости по 2 заводам:

Завод	Производство продукции, тыс. штук	Себестоимость 1 шт., руб.
I квартал	II квартал	I квартал	II квартал
I
II

Производство продукции, тыс. штук

Определим влияние на себестоимость изменения структуры совокупности.

Рассчитаем:

1) индекс себестоимости переменного состава;

2) индекс себестоимости постоянного состава.

Отметим, что себестоимость чаще всего обозначается буквой «Z».

Индекс себестоимости переменного состава исчисляется как отношение средней себестоимости за текущий период к средней себестоимости за базисный период.

(18× 90 + 100× 15) / (20× 80 + 18× 70) = 0,861

Индекс себестоимости переменного состава показывает снижение себестоимости на 13,9% в отчетный период по сравнению с базисным. Рассчитаем индекс себестоимости постоянного состава как агрегатный индекс:

(18× 90 + 15× 100) / (20× 90 + 18× 100) = 0,867.

Индекс показывает снижение себестоимости на 13,3% в отчетный период по сравнению с базисным. Сравнивая индекс переменного состава и индекс постоянного состава, определим индекс структурных сдвигов, т.е. индекс влияния на динамику средней себестоимости изменения структуры. Индекс структурных сдвигов равен частному от деления индекса переменного состава на индекс постоянного состава:

0,861 / 0,867 = 0,993.

Таким образом, изменение структуры привело к снижению себестоимости на 0,7%.

Индекс себестоимости переменного состава дает оценку изменения параметра с учетом влияния структурных сдвигов, а индекс себестоимости постоянного состава не учитывает этого влияния.

В менеджерской практике широко применяется индексный анализ. Особое место здесь занимают индексы цен, которые нужны при разработке бизнес-планов новых производств, без них невозможно обойтись при пересчете основных показателей деятельности предприятия из фактически действующих цен в сопоставимые. Индексы цен позволяют соизмерять динамику цен во времени и разброс в пространстве.

Важное место в статистике цен занимает индекс потребительских цен, отражающий реальную покупательную способность денег, которыми располагают различные слои населения для удовлетворения своих материальных, культурных и духовных потребностей. Методология исчисления этого индекса предполагает расчет отдельно для различных регионов, товарных групп и услуг, отдельных групп населения с различными уровнями доходов.

Пересчет важнейших показателей из фактических цен в сопоставимые, исключение влияния инфляции осуществляются с помощью индексов-дефляторов.

Например, чтобы определить реальную стоимость основных фондов предприятия в 2010 г. следует ОФ 2010 = ОФ 1 / I d, где ОФ 1 — номинальная стоимость в 2010 г., a I d — индекс-дефлятор, исчисляемый как отношение фактической стоимости ОФ отчетного периода к стоимости ОФ, структурно соответствующей текущей, но определенной в ценах базового периода.

Дата добавления: 2014-01-04