Лекция №4

Электрические цепи однофазного синусоидального тока.

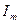Синусоидальный ток – ток, изменяющийся во времени по синусоидальному закону, имеющего следующий вид: , где - амплитудное (максимальное) значение тока за период, ; 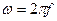- угловая частота, 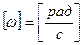; 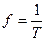- частота (число колебаний в секунду), 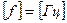; 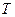- период (время, за которое происходит одно полное колебание), ; 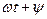- фаза, которая характеризует состояние колебания синусоиды в момент времени ; 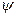- начальная фаза (фаза в момент времени ).

Любая синусоидальная функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.

Действующее значение синусоидально изменяющейся величины обозначается за 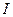и находится по следующей формуле: . На это значение реагируют приборы электромагнитной, электродинамической и тепловой систем.

Изображение синусоидально изменяющихся величин векторами на комплексной плоскости.

Ось называется осью действительных чисел, а ось 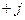называется осью комплексных чисел.

Нарисуем единичный вектор на комплексной плоскости . Комплексное число будет изображаться вектором, который численной равен единице и составляет с осью действительных чисел угол , который отчитывается от оси действительных чисел против часовой стрелки в положительном направлении.

По формуле Эйлера: 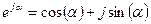. Умножив на 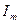получим вектор, который будет в 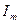раз больше единичного вектора: .

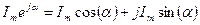Пусть , тогда , где ток 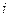- коэффициент при мнимой части комплексного числа 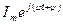, который также является проекцией вращающегося с частотой вектора на ось комплексных чисел.

На комплексной плоскости принято векторы синусоидально изменяющихся во времени величин изображать для момента времени . Подставив , получим 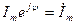, где 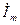- комплексная амплитуда тока 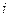, которая изображает ток 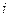на комплексной плоскости в момент времени .

Комплекс действующего значения: .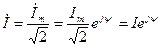

Пример:

Даны мгновенные значения токов:

;

;

;

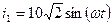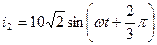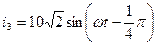Требуется:

1. Построить графики мгновенных значений.

2. Записать комплексные амплитуды и комплексные значения этих токов.

3. 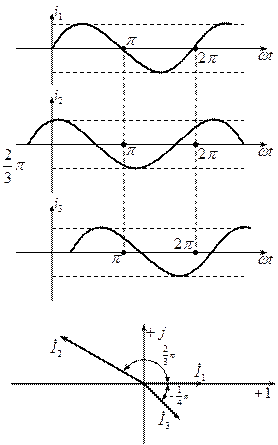Построить вектора токов на комплексной плоскости.

Ток 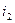опережает ток 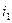по фазе на , поэтому начало 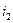сдвинуто влево на величину . Ток 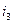отстаёт от ток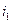а на , поэтому его начало сдвинуто вправо на величину .

Комплексные амплитуды токов: находятся следующим образом:

;

;

.

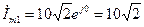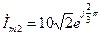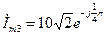Комплексы действующих значений токов, находятся следующим образом:

;

;

.

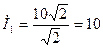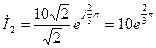Дан комплекс действующего значения тока .

Требуется записать мгновенное значение тока.

Мгновенное значение тока будет иметь следующий вид: .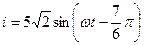

Элементы цепи синусоидального тока.

Элементами цепи синусоидального тока являются: резистор (сопротивление 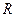), катушка индуктивности (индуктивность ) и конденсатор (ёмкость 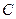). Сопротивление переменному току оказывают не только те элементы, в которых выделяется энергия в виде тепла, но и те элементы, в которых энергия не выделяется, а периодически запасается в электрических или магнитных полях. Такие элементы называются реактивными. Реактивными сопротивлениями являются индуктивность и ёмкость.

Синусоидальный ток в активном сопротивлении.

Мгновенное значение тока имеет следующий вид: 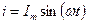. По закону Ома можно найти напряжение на активном сопротивлении: 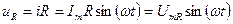, где - амплитудное напряжение. Комплекс действующего значения тока: 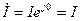. Комплекс действующего значения напряжения: .

На активном сопротивлении, то есть на резисторе, ток и напряжение совпадают по фазе, или, другими словами, разность фаз между током и напряжением равна нулю.

Мгновенная мощность определяется по формуле: . Так как ток и напряжение совпадают по фазе, то, очевидно, что мгновенная мощность всегда будет иметь положительное значение.

Схема замещения катушки индуктивности.

Допустим, что потери аналогичны.

Если через катушку индуктивности течёт синусоидальный ток 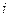, то в катушке возникает ЭДС самоиндукции: .

Положительное направление ЭДС самоиндукции совпадает с положительным направлением тока.

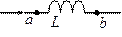Найдём разность потенциалов между точками 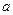и :

;

;

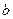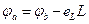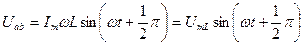, где 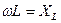- индуктивное сопротивление, которое прямо пропорционально частоте.

Положительное направление напряжения совпадает с положительным направлением тока. Комплекс действующего значения тока: 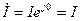. Комплекс действующего значения напряжения: 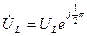. Комплекс действующего значения ЭДС самоиндукции: . Построим эти три вектора на комплексной плоскости:

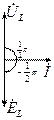Вывод: Напряжение на катушке на опережает по фазе ток, а ЭДС самоиндукции на по фазе отстаёт от тока.

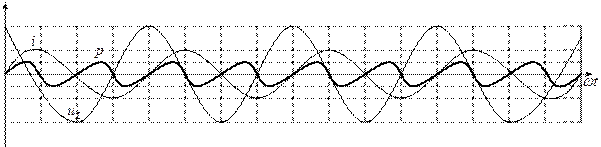
Мгновенная мощность определяется по формуле: . Энергия от источника в интервале поступает на создание магнитного поля в катушке индуктивности, а на интервале 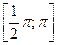энергия возвращается в источник.

Учтём активные потери:

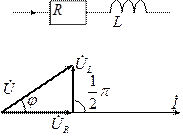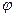Построим векторную диаграмму для этого участка. Так как ток будет одним и тем же, то построение диаграммы можно начать с построения вектора тока. Вектор напряжений строится по второму закону Кирхгофа: . Видно, что угол - положительный, что характерно для индуктивного типа цепи.

Дата добавления: 2014-01-04