
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормальные формы для формул алгебры высказываний
|
|
|
|
Пропозициональные переменные. Классификация формул.
В формулу (Х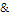 Y)
Y)  Z вместо переменных X, Y, Z можно подставлять конкретные высказывания, после чего вся формула будет превращаться в некоторое составное высказывание. Переменные, вместо которых можно подставлять высказывания, т.е. переменные, пробегающие множество высказываний, называют пропозициональными переменными, или высказывательными переменными, или переменными высказываниями.
Z вместо переменных X, Y, Z можно подставлять конкретные высказывания, после чего вся формула будет превращаться в некоторое составное высказывание. Переменные, вместо которых можно подставлять высказывания, т.е. переменные, пробегающие множество высказываний, называют пропозициональными переменными, или высказывательными переменными, или переменными высказываниями.
Теперь дадим точное определение формулы алгебры высказываний. Определение 2.1
1. Каждая отдельно взятая пропозициональная переменная есть формула алгебры высказываний.
2. Если F1 и F2 — формулы алгебры высказываний, то
выражения 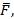 F1& F2, F1V F2, F1
F1& F2, F1V F2, F1 F2 , F1
F2 , F1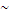 F2 ,также являются формулами алгебры высказываний.
F2 ,также являются формулами алгебры высказываний.
3. Никаких других формул алгебры высказываний, кроме получающихся согласно п. 1 и 2, нет.
Определения такого типа называются индуктивными.
Формулы алгебры высказываний подразделяются на следующие типы: выполнимые, тавтологии, опровержимые и тождественно ложные.
Формула алгебры высказываний называется выполнимой, если некоторая ее конкретизация является истинным высказыванием, т.е. существуют такие конкретные высказывания А1 , А2,..., Аn, которые, будучи подставленными в эту формулу вместо переменных Х1, Х2,..., Хn соответственно, превращают ее в истинное высказывание. Таким образом, F(X1 ,X2,..., Хn) выполнима, если существуют такие конкретные высказывания А1, А2,..., Аn, что 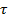 (F(A1,А2,..., Аn)) = 1.
(F(A1,А2,..., Аn)) = 1.
Формула F(X1,Х2,..., Хn) называется тавтологией, или тождественно истинной, если она превращается в истинное высказывание при всякой подстановке вместо переменных конкретных высказываний А1 , А2,..., Аn,т.е. если 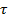 (F(A1,А2,..., Аn)) = 1 для любых высказываний
(F(A1,А2,..., Аn)) = 1 для любых высказываний
Формула F(X1,Х2,..., Хn)называется опровержимой, если существуют такие конкретные высказывания А1 , А2,..., Аn, которые превращают данную формулу в ложное высказывание F(А1 , А2,..., Аn.),т.е. 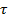 (F(A1,А2,..., Аn)) = 0. Другими словами, опровержимые формулы — это формулы, не являющиеся тавтологиями.
(F(A1,А2,..., Аn)) = 0. Другими словами, опровержимые формулы — это формулы, не являющиеся тавтологиями.
Наконец, формула F(X1,Х2,..., Хn)называется тождественно ложной, или противоречием, если 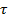 (F(A1,А2,..., Аn)) = 0 для любых конкретных высказываний A1,А2,..., Аn. Другими словами, тождественно ложные формулы — это такие формулы, которые
(F(A1,А2,..., Аn)) = 0 для любых конкретных высказываний A1,А2,..., Аn. Другими словами, тождественно ложные формулы — это такие формулы, которые
не являются выполнимыми.
. В алгебре логики важную роль играют следующие равенства:
1. Законы коммутативности (переместительности):
а) A &В 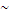 В & А - коммутативность конъюнкции;
В & А - коммутативность конъюнкции;
б) А V В 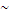 В V А - коммутативность дизъюнкции.
В V А - коммутативность дизъюнкции.
 2. Законы ассоциативности (сочетательности):
2. Законы ассоциативности (сочетательности):
а) (А&В) &С 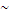 А & (В& С) - ассоциативность конъюнкции
А & (В& С) - ассоциативность конъюнкции
б) (А V 5) V С 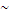 А V (В V С) - ассоциативность дизъюнкции
А V (В V С) - ассоциативность дизъюнкции
3. Законы идемпотентности:
а) А А 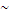 А - идемпотентность конъюнкции;
А - идемпотентность конъюнкции;
б) AV А 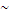 А - идемпотентность дизъюнкции.
А - идемпотентность дизъюнкции.
4. Законы дистрибутивности (распределительности):
а) А& (В V С) 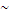 (А & В) V (А & С) - дистрибутивность конъюнкции относительно дизъюнкции;
(А & В) V (А & С) - дистрибутивность конъюнкции относительно дизъюнкции;
б) А V(В& С) 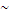 (А V Б) & (А V С) - дистрибутивность дизъюнкции относительно конъюнкции.
(А V Б) & (А V С) - дистрибутивность дизъюнкции относительно конъюнкции.
5. Свойства нуля и единицы:
а) А&0 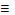 0;
0;
б) AV0 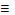 A;
A;
в) A&1 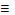 A;
A;
г) АV1 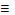 1.
1.
6. 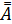
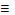 A - правило снятия двойного отрицания.
A - правило снятия двойного отрицания.
7. Законы де Моргана;
 а) А& В
а) А& В 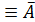 V
V 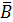 ;
;
б) 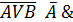
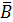
8. A 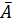
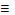 0 - закон противоречия.
0 - закон противоречия.
9. А V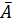 = 1 - закон исключённого третьего.
= 1 - закон исключённого третьего.
10. Законы поглощения:
а) А & (А V В) 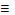 А;
А;
б) AV(A&B)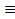 A.
A.
11. Правила склеивания-расщепления:
а) (А V 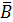 ) & (А V
) & (А V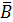 )
) 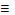 А;
А;
б) (A&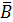 )V(A&B)
)V(A&B) 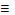 A
A
12. AB 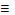
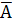 V В - выражение импликации через дизъюнкцию и отрицание.
V В - выражение импликации через дизъюнкцию и отрицание.
13. А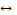 В
В 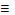 (А
(А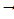 В) (В
В) (В 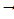 А) - выражение эквивалентности через конъюнкцию и импликацию.
А) - выражение эквивалентности через конъюнкцию и импликацию.
14. Выражение эквивалентности через конъюнкцию, дизъюнкцию и отрицание:
а) А 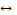 В
В 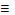 (А & В) V (
(А & В) V (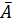 &
& 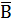 );.
);.
б) A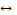 B
B 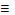 (
(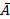 VB)&(AV
VB)&(AV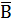 );.
);.
Множество всех булевых в базисе S1={¬, &, V} образуют булеву алгебру. Все формулы в этой алгебре можно записать с помощью этих трех связок.
Для каждой формулы алгебры высказываний можно указать равносильную ей формулу, содержащую из логических связок лишь отрицание, конъюнкцию и дизъюнкцию. Для этого нужно, используя равносильности выразить все имеющиеся в формуле импликации и эквивалентности через отрицание, конъюнкцию и дизъюнкцию.
Нормальные формы являются синтаксически однозначным способом записи формулы, реализующей заданную функцию.
Если x логическая переменная, а  ,то выражение
,то выражение

называется литерой.
Литеры х и ┐х называются контрарными. Конъюнктом называется конъюнкция литер. Дизъюнктом называется дизъюнкция литер. Например, формулы x y ┐z и х у х ┐х являются конъюнктами, формулыxVyV┐z и xVyV┐x - дизъюнктами, а формула ┐z является одновременно и конъюнктом и дизъюнктом.
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция конечного числа конъюнктов.
Конъюнктивной нормальной формой (КНФ) называется конъюнкция конечного числа дизъюнктов.
Более просто: ДНФ - это сумма произведений, а КНФ - это произведение логических сумм
Литеры х и ┐х называются контрарными. Конъюнктом называется конъюнкция литер. Дизъюнктом называется дизъюнкция литер. Например, формулы x-y-z и х у х х являются конъюнктами, формулы xvyvz и xvyvx - дизъюнктами, а формула z является одновременно и конъюнктом и дизъюнктом.
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция конечного числа конъюнктов.
Конъюнктивной нормальной формой (КНФ) называется конъюнкция конечного числа дизъюнктов.
Более просто: ДНФ - это сумма произведений, а КНФ - это произведение логических сумм
Примеры.
1. X yVyzVx — это ДНФ (сумма произведений).
2. (хV ┐у V ┐z)• (хVу)• z —это КНФ (произведение сумм).
3. ┐xVyVzV┐w — это ДНФ и КНФ (одновременно).
4. ┐х • у • ┐z • w — это ДНФ и КНФ (одновременно).
5. (xVxVy)(yVzVx)-z — это КНФ.
6. x y ┐z и х у х ┐х — это ДНФ.
7.  х (х V yz) x-┐y-z — это не нормальная форма (не ДНФ и не КНФ).
х (х V yz) x-┐y-z — это не нормальная форма (не ДНФ и не КНФ).
Пусть функция f записана в базисе S1. Данная функция приводится к нормальной форме следующим путем:
1) используем законы де Моргана, чтобы преобразовать формулу к виду, в котором знаки отрицания относятся только к отдельным переменным;
2) применяем правило снятия двойного отрицания: ┐┐x=x;
3) далее использовать законы дистрибутивности, причем необходимо использовать первый закон дистрибутивности для приведения к ДНФ
HI & (H2VH3)=(H1 &H2)V(H1 &НЗ),
и второй закон дистрибутивности для приведения к КНФ.
H1V(H2&H3)=(H1VH2)&(H1VH3).
Любая булева функция может иметь бесконечно много представлений в виде ДНФ и КНФ. Например, используя дополнительно законы инверсий и правила операций с константами можно добиться, чтобы в каждом отдельном конъюнкте или дизъюнкте любая переменная входила бы не более одного раза (либо сама либо ее отрицание).
Пример 1. Для приведения к ДНФ используем 1-ый закон дистрибутивности.
 x ┐y x y ┐z (yVz)=x ┐y (┐xV┐yV┐┐z) (yVz)=(x┐y┐xVx┐y┐yVx┐yz)-(yVz)= -это КНФ
x ┐y x y ┐z (yVz)=x ┐y (┐xV┐yV┐┐z) (yVz)=(x┐y┐xVx┐y┐yVx┐yz)-(yVz)= -это КНФ
= (0 V х ┐у V х ┐у z) (у V z) = (х ┐у V х ┐у z) (у V z) = это другая
КНФ
= x┐yyVx┐yzyVx┐yzVx┐yzz = 0V0Vx┐yzVx┐yz =
=x┐yzVx┐yz -это ДНФ
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 997; Нарушение авторских прав?; Мы поможем в написании вашей работы!