
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кванторы, их свойства
|
|
|
|
Пусть P(xi,x2,...,xn) — n-местный предикат, определенный на М. Зафиксируем xi=а. Определим (n-1)-местный предикат Q(x1,x2,...,xk_1, xk+1,xn) следующим образом: Q(x1,x2,...,xk_i, xk+i,xn)=P(x1,x2,...,xk+1.,a,xk+1, xn). Говорят, что предикат Q(x1,x2,...,xk-1, xk+1,xn) получен из предиката P(x1,x2,...,xn) фиксацией значения i-й переменной:xi =а.
Определение 1. Пусть Р(х) — одноместный предикат. Поставим ему в соответствие высказывание, обозначаемое 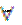 xP(x) (читается «для любого х Р(х)»}, которое истинно тогда и только тогда, когда Р(х) — тождественно истинный предикат. О высказывании
xP(x) (читается «для любого х Р(х)»}, которое истинно тогда и только тогда, когда Р(х) — тождественно истинный предикат. О высказывании 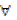 хР(х) говорят, что оно получено из предиката Р навешиванием квантора всеобщности по переменной х.
хР(х) говорят, что оно получено из предиката Р навешиванием квантора всеобщности по переменной х.
Определение 2. Пусть Р(х) — одноместный предикат. Поставим ему в соответствие высказывание, обозначаемое 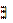 хР(х) (читается «существует х Р(х)»), которое ложно тогда и только тогда, когда Р(х) — тождественно ложный предикат. О высказывании
хР(х) (читается «существует х Р(х)»), которое ложно тогда и только тогда, когда Р(х) — тождественно ложный предикат. О высказывании 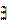 хР(х) говорят, что оно получено из предиката Р навешиванием квантора существования по переменной х.
хР(х) говорят, что оно получено из предиката Р навешиванием квантора существования по переменной х.
Замечание 1. Обозначения 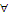 и
и 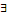 для кванторов — это перевернутые латинские буквы А и Е соответственно, которые являются первыми буквами в английских словах АLL — все, Exist — существовать.
для кванторов — это перевернутые латинские буквы А и Е соответственно, которые являются первыми буквами в английских словах АLL — все, Exist — существовать.
Замечание 2. Высказывания можно считать предикатами, не содержащими переменных, т. е. 0-местными предикатами (или предикатами любой местности).
Пусть P(x1,x2,...,xn) — n-местный предикат, определенный на М. Зафиксируем в нем значения переменных x1,x2,...,xk-1,xk+1,xn. На полученный одноместный предикат Q(xK) навесим квантор всеобщности (существования), получим высказывание. Тем самым фиксированному набору значений переменных x1,x2,...,xk_i,xk+i,xn с помощью квантора всеобщности (существования) поставлено в соответствие высказывание. Говорят, что этот (n-1)-местный предикат переменных x1,x2,...,xk.1,xk+1,xn получен из исходного предиката P(x1,x2,...,хn) навешиванием квантора всеобщности (существования) по k-й переменной. Этот предикат обозначают: 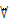 xKP(x1,x2,...,xn) (
xKP(x1,x2,...,xn) (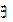 хк P(x1,x2,...,xn)). Об к-й переменной (которой уже нет) говорят, что она связана квантором всеобщности (существования).
хк P(x1,x2,...,xn)). Об к-й переменной (которой уже нет) говорят, что она связана квантором всеобщности (существования).
Обычно, связки и кванторы упорядочиваются по приоритету следующим образом ┐,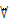 ,
, 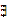 , &, V,
, &, V,
Теорема 2.2.Разноименные кванторы, вообще говоря, не коммутируют.
Теорема 2.3. (основные равносильности, содержащие кванторы) Имеют место следующие равносильности:
Законы де Моргана
Коммутативность
Дистрибутивность
Ограничения действия кванторов
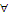 x(P(x) V Q(y)) =
x(P(x) V Q(y)) = 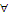 xP(x) V
xP(x) V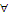 xQ(y),
xQ(y), 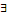 x(P(x)&Q(y) =
x(P(x)&Q(y) = 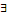 xP(x) &
xP(x) & 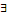 xQ(y)
xQ(y)
Для любого двухместного предиката 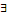 у
у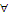 xP(x, у)
xP(x, у) 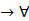 x
x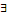 yP(x, у) = 1
yP(x, у) = 1
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2915; Нарушение авторских прав?; Мы поможем в написании вашей работы!