Вывод ФРС системы из структурной схемы

В зависимости от сложности и строения системы существует множество способов для получения логической ФРС. В наиболее простом случае ФРС можно сразу «выписать» на основе структурной схемы. Например, для следующей схемы

ФРС будет равна 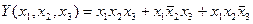. Здесь умножение является булевой операцией И, а сложение – операцией ИЛИ, обозначает отрицание значения переменной. Каждое из логических слагаемых в полученной ФРС выражает одно из трех работоспособных состояний системы.

Рассмотрим базовый подход получения ФРС по структурной схеме. Пусть даны ФР и для двух подсистем (или отдельных элементов) общей системы. В этом случае ФР общей системы 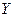равняется:

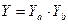• - объединение через логическое И - если подсистемы (или элементы) соединены последовательно, т.е. для работоспособности системы необходима работоспособность обоих подсистем;
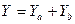• - объединение через логическое ИЛИ - для параллельного соедениния, т.е. когда для работоспособности системы достаточно работоспособности хотя бы одной подсистемы.

Кроме того возможен случай кратного резервирования. Например, для работы системы необходима работоспособность двух из трех подсистем A, B и C. Тогда минимальные необходимые наборы работоспособных подсистемы будут равны AB, BC и AC. Итоговая ФРС тогда будет иметь вид: .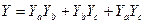

Рассмотрим эти правила на примере следующей системы.

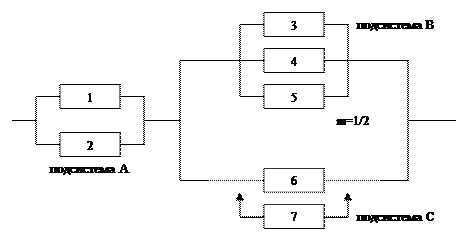
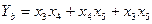
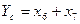
Для простых схем этот метод удобен. Но для больших структурно-сложных систем, содержащих множество элементов и агрегатов, такой подход становится слишком трудоемким а иногда просто неприменимым. Поэтому создаются формальные методы вывода ФРС, которые могут быть реализованы на ЭВМ. Рассмотрим некоторые из них.

Дата добавления: 2014-01-03