Расчет элементов, работающих на центральное и местное сжатие

При центральном сжатии в поперечном сечении эле­мента возникают напряжения, которые равномерно рас­пределяются по сечению (рис. 19.2,а). В данном случае потери несущей способности возможны не только из-за утраты прочности кладки, но и вследствие потери ус­тойчивости элемента. Прочность центрально-нагружен­ного элемента малой гибкости рассчитывают по следующему условию:

N ≤ RA, (19.13)

где R — расчетное сопротивление кладки; А — площадь поперечно­го сечения.

В гибких элементах разрушение может произойти от потери устойчивости при напряжениях в сечении, которые значительно меньше предельных, допускаемых ус­ловием прочности σ<R. Как уже отмечалось выше, та­кая возможность учитывается введением в расчет коэф­фициента продольного изгиба φ<1, зависящего от гибкости элемента λ. Она, в свою очередь, определяется, как отношение расчетной длины к наименьшей стороне сечения (для прямоугольного сечения) или к меньшему радиусу инерции (для произвольного сечения)

λ_h=l₀ /h; λ_і=l₀ /і_mіn (19.14)

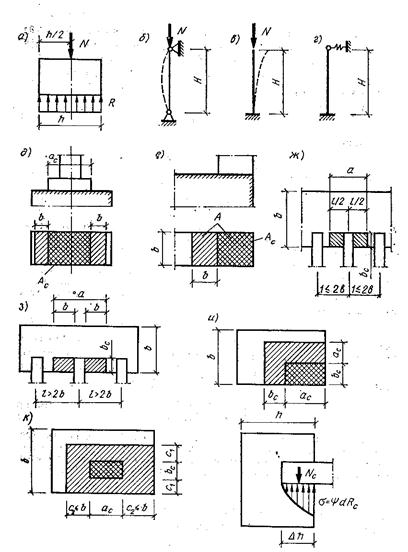
Рис. 19.2. Схемы к расчету элементов из каменной кладки на цент­ральное и местное сжатие

а — эпюра напряжений; 6, в, г — расчетная высота каменных стен при раз­личных условиях закрепления; д — расчетная площадь сечения площади смя­тия при местной нагрузке, распределяемой по всей толщине стены; е — то же при нагрузке, действующей по краю стены; ж, з — то же, при опирании на стену концов балок и прогонов; и — то же, при местной краевой нагрузке, действующей на угол элемента; к — то же при приложении местной нагрузки на некотором участке по длине и ширине элемента.

Гибкость элементов каменных конструкций дополни­тельно зависит и от упругой характеристики кладки а, Значения коэффициентов продольного изгиба приведены в табл. 19.1.

Расчетная высота каменных стен, колонн и столбов зависит от условий их закрепления в опорных зонах. При шарнирном опирании на опоры, неподвижные в гори­зонтальном направлении (перекрытия жилых зданий) принимают l₀ = Н (Н — высота этажа, рис. 19.2,б). Для свободно стоящих конструкций, в которых отсутствует связь с перекрытиями или другими горизонтальными опо­рами, l₀ = 2H (рис. 19.2, в).

Таблица 19.1. Коэффициенты продольного изгиба каменной кладки

Гибкость элемента	Коэффициенты φ при упругой характеристике α
λh	λі
					0,98	0,97	0,9	0,82
		0,98	0,96	0,95	0,91	0,88	0,81	0,68
		0,95	0,92	0,9	0,85	0,8	0,7	0,54
		0,92	0,88	0,84	0,79	0,72	0,6	0,43
		0,88	0,84	0,79	0,72	0,64	0,51	0,34
		0,85	0,79	0,73	0,66	0,57	0,43	0,28
		0,81	0,74	0,68	0,59	0,5	0,37	0,23
		0,77	0,7	0,63	0,53	0,45	0,32	—
		0,69	0,61	0,53	0,43	0,35	0,24	—
		0,61	0,52	0,45	0,36	0,29	0,2	—
		0,53	0,45	0,39	0,32	0,25	0,17	—
		0,44	0,38	0,32	0,26	0,21	0,14	—
		0,36	0,31	0,26	0,21	0,17	0,12	—
		0,29	0,25	0,21	0,17	0,14	0,09	—
		0,21	0,18	0,16	0,13	0,2	0,07	—
		0,17	0,15	0,13	0,1	0,08	0,05	—
		0,13	0,12	0,1	0,08	0,06	0,04	—

При упругой верхней опоре и нижней защемленной (рис. 19.2, г) l₀ = 1,25H — в однопролетных зданиях и l₀ =1,25Н — в многопролетных.

Условие расчета неармированных центрально-сжа­тых элементов по несущей способности имеет следую­щий вид:

N ≤ m_gφRA (19.15)

где т_g — коэффициент, учитывающий влияние прогиба при длитель­но действующей нагрузке; φ — коэффициент продольного изгиба, определимый по табл. 19.1.

Неоднородность кладки и неточность монтажа при­водят к тому, что физически невозможно точно совме­стить точку приложения внешней силы с осью элемента, поэтому всегда существует некоторый случайный экс­центриситет e_о, который для толстых стен (более 25 см) не учитывается. В тонких гибких элементах в случаях длительного действия нагрузки развивается ползучесть кладки, вызывающая постепенное отклонение элементов от персонального положения и приводящая к увеличе­нию случайных эксцентриситетов, а следовательно, и возрастанию изгибающих моментов, вызываемых этими эксцентриситетами. Это снижает прочность кладки.

Значение коэффициента m_g принимают равным еди­нице, если меньшая сторона поперечного сечения h ≥ 30 см или меньший радиус инерции і≥ 8,7 см. Во всех остальных случаях (при е₀ =0) значение коэффициента определяют по формуле

m_g=1-ηN_g/N, (19.16)

где η — коэффициент, учитывающий вид кладки и процент продоль­ного армирования (определяется по табличным данным СНиПа); N_g — расчетная продольная сила от длительно действующей на­грузки.

Алгоритм и блок-схема расчета центрально-сжатого элемента из каменной кладки не будут принципиально отличаться от алгоритма для расчета стального стерж­ня. Разница будет заключаться в том, что значение про- чности R и коэффициента продольного изгиба φ следует определять для принятых марки и сечения каменной кладки, кроме того, при расчете требуется дополнитель­но вычислять значение коэффициента.

Местное сжатие (смятие) кладки происходит в зонах опирания балок, прогонов, ферм, колонн, плит покры­тий и перекрытий, а также других конструкций. На­грузка в этом случае воспринимается не всем попереч­ным сечением поддерживающей конструкции, а частью этого сечения, поэтому несущая способность кладки при местном сжатии всегда выше, чем при осевом, когда в работе участвует все поперечное сечение элемента (рис. 19.2, д — к). Это объясняется тем, что соседние ненагру­женные участки кладки препятствуют развитию попе­речных деформаций нагруженного участка, повышая тем самым его местное сопротивление.

При местном сжатии расчетное сопротивление клад­ки определяют по следующей формуле:

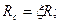
(19.17)

здесь R — расчетное сопротивление кладки осевому сжатию; А — расчетная площадь сечения; А_с — площадь смятия, через которую воспринимается нагрузка; ξ₁—предельный коэффициент, учитыва­ющий максимально возможное увеличение R_c по сравнению с R и зависящий от схемы расположения площади смятия и вида кладки, ξ₁ =1...2 (определяется по табличным данным СНиПа).

Вычисление площадей А и А_с. Площадь смятия А_с определяется непосредственно размером опорных пло­щадок, по которым соприкасаются конструкции. Если в опорной зоне используют бетонные, железобетонные или металлические прокладки, то А_с принимают равной пло­щади прокладки. Расчетная площадь сечения включа­ет в себя помимо площади смятия дополнительные пло­щади соседних участков кладки, участвующие в работе:

при местной нагрузке, распределяемой по всей тол­щине стены

(рис. 19.2, д),

А = А_С + 2b²;

при нагрузке, действующей по краю стены (рис.19.2, е),

А = А_с + b ²;

при опирании на стену концов балок и прогонов (рис,19.2, ж, з)

А = ab_с ,

при местной краевой нагрузке, действующей на угол элемента (рис.19.2, и),

А = (а_с + b_c)² при (а_с + b_c) ≤ b

A=b (а_с + b_c) при (а_с + b_c) > b;

при местной нагрузке, приложенной на некотором участке по длине и ширине элемента (рис. 19.2, к):

А = (b_c+2_с1)(а_с + 2_c2).

Если площадь смятия располагается от края стены на расстояние больше, чем b, принимают с₂= b;

несущую способность кладки при местном сжатии рассчитывают по условию

N_с ≤ ψdR_сA_с (19.18)

где ψ, d — соответственно коэффициент полноты эпюры давления от местного загружения и коэффициент, учитывающий вид кладки.

При отсутствии распределительных плит под концами прогонов и балок местное давление на стену переда­ется неравномерно, поэтому для кладки из кирпичей, сплошных бетонных камней, крупных блоков из тяжелого бетона и бетона на пористых заполнителях разреша­ется принимать ψ d = 0,75; для пустотелых бетонных кам­ней и блоков, а также блоков из ячеистого бетона ψ d=0,5. При равномерном распределении давления по площади смятия принимают ψ = 1, при треугольной эпюре ψ = 0,5. Коэффициент d имеет значения 0,5.. 1,5 в зависимости от типа кладки.

Дата добавления: 2014-01-04