Ряды максимальных расходов Qi , м3/с

Пример

Исходные данные:

Для выбранного варианта из прил. 1 используем два ряда параллельных наблюдений по реке А и В продолжительностью 11 лет (1992 – 2002 гг.).

1. Установлено, что река А может являться рекой-аналогом, так как отвечает требованиям, предъявляемым к рекам-аналогам, и имеет более длительный период гидрометрических наблюдений по сравнению с рекой В.

Для приведения кратковременных наблюдений на реке В к многолетнему периоду применим метод парной регрессии.

Результаты расчета параметров, необходимых для определения коэффициентов корреляции и регрессии, сведены в табл. 3.

Вычислим средние значения:

Хс = ∑Х_i / 11 = 3801 / 11 = 345,5 м³/с;

Yc = ∑ Y_i / 11 = 2245/ 11 = 204,1 м³/с.

Отклонения от средних арифметических значений будут равны:

Δ Xi = Хi – Xc; Δ Yi = Yi – Yc.

Коэффициент корреляции определим по формуле (6):

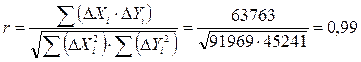
Таблица 3

Годы	Xi, м^3/с	Yi, м^3/с	Δ Xi, м^3/с	Δ Yi, м^3/с	Δ Xi *Δ Yi,	Δ Xi ^2	Δ Yi ^2
			28.5 -145.5 0.5 145.5 126,5 -16,5 -43,5 131,5 -100,5 -85 -117,5	-13.1 -80.1 -11.1 76.9 110,9 -31,1 -53,1 103,9 -67,1 -1,1 -35,1	-373 -6
-	∑ Xi = 3801	∑ Yi = 2245	-	-	∑Δ Xi *Δ Yi =63763	∑Δ Xi ^2 =91969	∑Δ Yi ^2 =45241

Среднее квадратическое отклонение коэффициента корреляции составит:

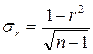
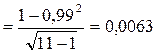
Критерий достоверности (не случайности) коэффициента корреляции равен:

К _д = r / σ_r = 0,99 / 0,0063 = 157.

Для удлинения ряда воспользуемся уравнением регрессии (7), в котором:

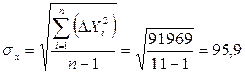
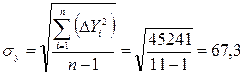
Таким образом, выполнены условия возможности применения метода парной регрессии для удлинения данного гидрологического ряда, т.е.: коэффициент корреляции r > 0.7 и коэффициент достоверности корреляции К _д > 2.

2. Прямую связи расходов рек А и В построим по двум значениям X _i, охватывающим весь ряд наблюдений на реке А:

X ₁ = 600 м³/с. Эта величина больше X_max = 576 м³/с.

Х ₂ = 150 м³/с. Эта величина меньше Х_min = 185 м³/с.

Y ₁ = 204,1 + 0,99 * (67,3/95,9) * (600 – 345,5) = 379,7 м³/с;

Y ₂ = 204,1 + 0,99 * (67,3/95,9) * (150 – 345,5) = 69,2 м³/с.

После построения прямой связи, нанесем на график точки с соответствующими значениями X_i и Y_i, которые должны находиться рядом с прямой (рис. 2).

3. По уравнению регрессии (7) определим 20 недостающих расходов воды (до n = 31) в реке В для соответствующих значений расходов воды в реке А. Определенные значения расходов воды в реке В, заключенные в скобках, приводятся в отчете.

Река (В), Y_i, м³/с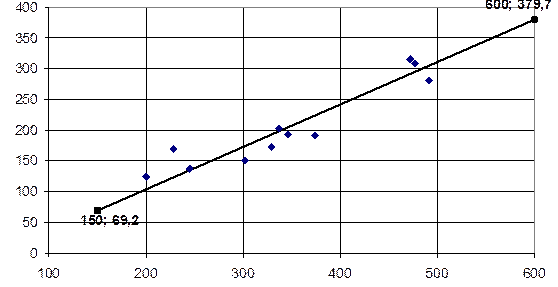

Река (А), X_i, м³/с

Рис. 2. Прямая связи расходов рек А и В. (Точками показаны расходы воды за 11 лет параллельных наблюдений).

Литература

1. СП 33-101-2003. Определение основных расчетных гидрологических характеристик. Госстрой России. М., 2004.

2. Пособие по определению расчетных гидрологических характеристик». - Л., Гидрометеоиздат, 1984.

3. Ресурсы поверхностных вод СССР. Ч. 1-2. Л., Гидрометеоиздат, 1972-75.

4. Железняков Г.В. и др. Гидрология, гидрометрия и регулирование стока. – М., Колос, 1984.

5. Гидрология и гидротехнические сооружения: Уч. для Вузов / Г.Н. Смирнов и др. М., Высш. шк., 1988.

6. СП 11-103-97. Инженерно-гидрометеорологические изыскания. Госстрой России. М., 1998.

7. СНиП 2.04.03 - 85. Канализация. Наружные сети и сооружения. М., 1986.

8. Андреев О.В. и др. Русловые и гидравлические расчеты при проектировании переходов через водотоки. Уч. пособие. М., 1989.

Приложение 1

Варианты заданий.

Год	Вариант
Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с

Продолжение прил. 1

Год	Вариант
Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с

Продолжение прил. 1

Год	Вариант
Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с

Продолжение прил. 1

Год	Вариант
Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с

Продолжение прил. 1

Год	Вариант
Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с

Продолжение прил. 1

Год	Вариант
Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с

Продолжение прил. 1

Год	Вариант
Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с	Река А, xi м^3/с	Река В, уi, м^3/с

Приложение 2

Номограммы для вычисления кривых трехпараметрического гамма-распределения методом наибольшего правдоподобия [10]

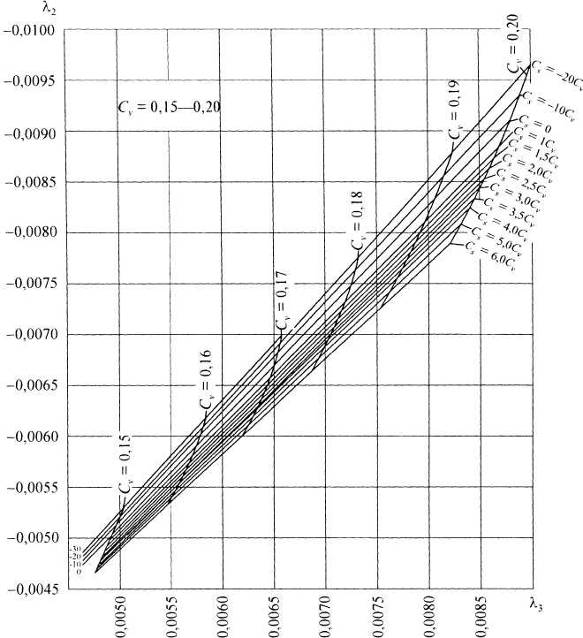
Дата добавления: 2014-01-04