Ленточный вакуум-фильтр

промывка суспензия

осадок фильтрат

Достоинство - высокая эффективность. Недостаток - сложность конструкции.

Тепловые процесы

1 Общая характеристика тепловых процессов.

Технические процессы, скорость которых определяется скоростью подвода или отвода тепла, называются тепловыми процессами, а аппараты для проведения таких процессов называются тепловыми аппаратами. К тепловым процессам относятся:

1) нагревание – повышение температуры перерабатываемого материала путём подвода к нему тепла;

2) охлаждение – понижение температуры перерабатываемых материалов путём отвода от них тепла;

3) конденсация – снижение паров, какого либо вещества путём отвода от него тепла;

4) испарение тепла – перевод в парообразное состояние какой-либо жидкости путём подвода к ней тепла.

Частным случаем испарения является процесс выпаривания, когда концентрация растворов увеличивается в результате удаления части растворителя в виде паров.

В тепловых процессах взаимодействует не менее чем две среды с различными температурами, при этом тепло передаётся самопроизвольно, без затраты работы, только от среды с большей температурой к среде с меньшей температурой.

Теплоносителем называется среда с высокой температурой, отдающая при теплообмене тепло.

Среда, воспринимающая при теплообмене тепло и имеющая более низкую температуру называется холодильным агентом.

Основной характеристикой любого теплового процесса является количество предаваемого тепла, от чего зависит размер тепловой аппаратуры, а основным размером тепловой аппаратуры является поверхность теплообмена.

Основное уравнение теплоотдачи:

,

где К_Л – коэффициент теплопередачи.

Для установившегося теплообмена имеем:

,

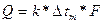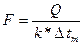
Тогда движущей силой теплового процесса является разница температур между теплоносителем и хладагентом.

Выясним, как определяются Q и:

Q – определяется из теплового баланса

Например:

Нам необходимо испарить w кг воды, вода имеет начальную температуру Т₁.

1) ;

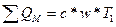2) Q_ПР = Q_ИСП = Q_НАГР;

Уравнение Клаузиуса:

;

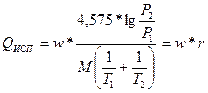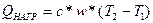
3) ;

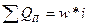4) Q₄ – обычно прим.

Другими словами при составлении тепловых балансов необходимо учитывать тепловые эффекты, сопровождающие процесс.

К ним относятся:

1) теплота испарения;

2) теплота химической реакции;

Закон Гесса:

,

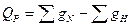где g_H - сумма теплот образования соединений вступающих в реакцию;

g_N - сумма теплот образования получающихся соединений.

3) теплота плавления:

Q_ПЛ = 13,5 Т_ПЛ/М;

4) теплота растворения:

,

где с₁ и с₂ – раствор. при Т₁ и Т₂

Определение

t₁^/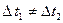

t₂^/ t₂^//

t₁ ^//

В общем случае , но как видно из рисунка не постоянно вдоль поверхности теплообмена. Потому необходимо рассчитать .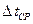

Могут быть различные случаи движения теплоносителя и хладагентов.

1) Параллельный ток;

2) Противоток;

3) Перекрёстный ток;

4) Смешанный.

Рассмотрим параллельный ток:

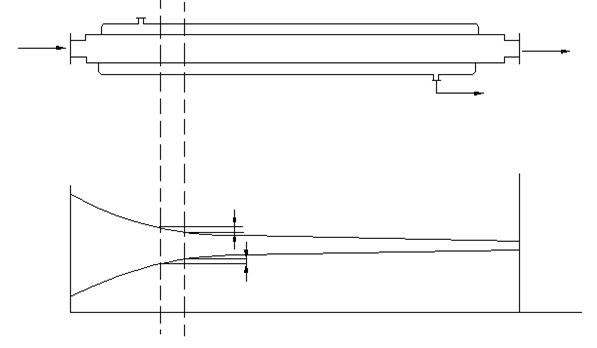t₁^/

t₂

dt₁ t₁^//

t₂^//

dt₂

t₂^/ t₂

dF F

dQ = k*(t₁-t₂)*dF (1)

В результате теплообмена теплоноситель отдаёт тепло dQ

dQ = -w₁*c₁*dt₁

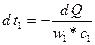(2)

А хладагент принимает тепло dQ

dQ = w₂*c₂*dt₂

(3)

Вычтем из равенства 2 равенство 3 и получим:

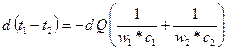(4)

Затем, заменив значение из (1) имеем:

(5)

согласно тепловому балансу:

(6)

Подставляя в (5) из (6) значения w₁*c₁ и w₂*c₂ получим:

(7)

Проинтегрируем выражение (7)

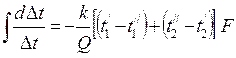
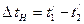
и получим:

следовательно:

(8)

Для противотока, если выводить, получим точно такое же выражение. При незначительном изменении температуры теплоносителя, когда 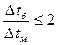, то

,

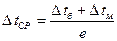ошибка < 4%.

При перекрёстном токе 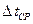определяем по формуле (8), но вводят поправку на коэффициент

,

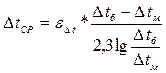а определяется из графика, например:

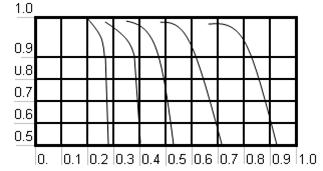
R=4 3 2 1,5

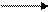Р

;

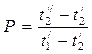Тепло передаётся в процессах теплообмена тремя способами:

1) Теплопроводностью – колебательным движением частиц;

2) Конвекцией – движение молекул;

3) Излучение – электромагнитные волны.

Практически передача тепла происходит 2-3 способами одновременно, т.е. происходит сложный теплообмен, необходимо знать закономерности всех видов теплообмена в чистом виде.

Теплопроводность

Распространение тепла теплопроводностью происходит при неравенстве температур внутри рассматриваемого тела (среды). Температурное поле в общем случае определяется функциональной зависимостью:

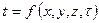
Если температура не изменяется во времени, то температурное поле стационарно (установившееся), если температура изменяется во времени, то нестационарное поле (неустановившееся). На практике кроме трёхмерного температурного поля, есть двух- и одномерные температурные поля, т.е. поля, являющиеся функциями двух и одной координат.

Температурный градиент:

t = const t₂ = const

изотермическая

поверхность

Закон Фурье

На основании экспериментов по изучению теплопроводности Фурье установил

,

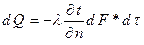где - коэффициент теплопроводности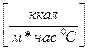

Коэффициенты теплопроводности для различных веществ различны и зависят от температуры и давления

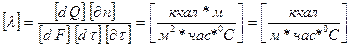
Для газов: Для жидкости: Для металлов:

0,005 – 0,15 0,08 – 0,6 2 – 360

Дифференциальное уравнение теплопроводности

z

Q_Z + dz

Q_y

t

Q_x dz Q_X + dx

Q_y + dy Q_Z

x

y

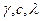- не изменяются по направлениям и во времени.

Согласно закону сохранения энергии:

Но согласно закону Фурье:

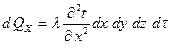
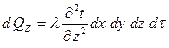
И тогда:

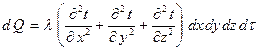
Согласно закону сохранения энергии dQ идет, не изменяя теплосодержание параллельно за время 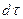, т.е.

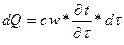, но

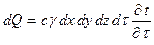и тогда

,

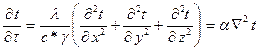где 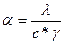- коэффициент температурной проводимости;

Теплопроводность плоской стенки

Рассмотрим установившийся тепловой режим, как наиболее часто встречающийся в практике.

Уравнение для передачи тепла через плоскую стенку можно вывести двумя способами:

1 вариант

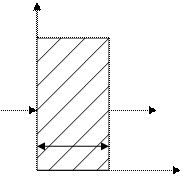t

Q Q

t₂

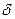
0 X

x₁ x₂

t₁ t₁ >t₂

- установившийся режим и одномерное поле,

,

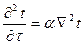тогда

,

т.к. .

Интегрируя, получим:

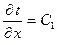или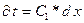

t = C₁x + C₂ – это уравнение прямой, следовательно t изменяется прямолинейно.

Определим константы интегрирования. Для этого напишем граничные условия:

(x = x₁ = 0; t = t₁); (x = x₂ = 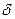; t = t₂), тогда

с₂ = t₁, a 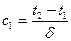и тогда уравнение прямой:

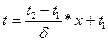
Отсюда получаем:

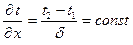
подставим в уравнение Фурье и получим:

Q = [ ккал ]

2 вариант

Плоская однослойная стенка

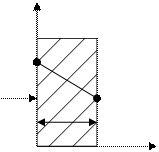t

t₁

t₂

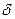
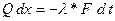
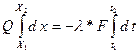
т.к. 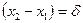, тогда

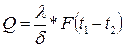
Для многослойной стенки: t

t₁ t₂

Q Q

t₃

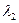
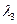
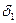
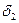
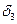x

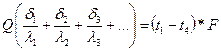
тогда

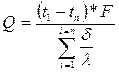
Теплопроводность цилиндрической стенки

d₂

t_в

t_M

В общем случае F = f (S) и тогда

Для цилиндрической стенки

, а 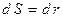, тогда

;

;

,

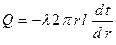
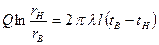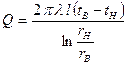или, заменив r на d получим

.

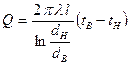Умножим и разделим правую часть выражения на (d_H – d_B), тогда

,

где или

Последнее выражение аналогично и для плоской стенки.

Конвективный теплообмен.

Под конвективным теплообменом понимают процесс распространения тепла в жидкости (газе) от поверхности твёрдого тела или к его поверхности одновременно конвекцией и теплопроводностью. Такой случай передачи тепла просто называют теплоотдачей. Основным законом теплоотдачи является закон Ньютона:

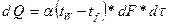
При установившемся теплообмене

Обычно практически постоянно и тогда:

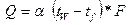
Рассмотрим модель теплоотдачи:

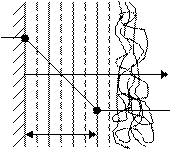
t_W

dQ

dF

X t_f

Опыт показывает, что у стенки всегда имеется ламинарная плёнка жидкости, хотя толщина её очень мала, и перепад температур имеет место в близи стенки. Следовательно, тепловой поток у стенки передаётся теплопроводностью, а дальше конвекцией. Представим себе такую толщину ламинарной плёнки (действительная + абстрактная) и назовём её эквивалентной ламинарной плёнкой. Эта плёнка имеет такую толщину, что на её границе температура равна температуре потока, тогда:

;

с другой стороны, согласно закону Ньютона:

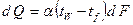
и следовательно:

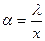
Из этого следует, что чем выше турбулентность потока, тем выше т.к. х уменьшается. Из всего сказанного выше ясно, что решение задач по теплоотдаче сводится к определению , что основано на эмпирических данных.

Критериальное уравнение конвективного переноса тепла.

Согласно рисунку можно написать:

Закон Фурье

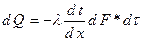
Закон Ньютона

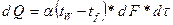
Дифференциальное уравнение, характеризующее условия на границе

Выведем уравнение, описывающее процесс распространения тепла в движущейся среде. При конвективном теплообмене, как было показано выше, тепло распространяется конвекцией и теплопроводностью. Тогда полное изменение температуры движущегося элемента можно записать:

,

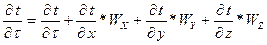где W_х W_у W_z – скорости движущихся элементов относительно осей.

И тогда, заменив в уравнение теплопроводности локальное изменение температур полным, получим дифференциальное уравнение конвективного переноса тепла Фурье – Кирхгоффа:

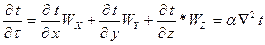
Таким образом, мы имеем два дифференциальных уравнения, описывающих конвективный теплообмен.

,

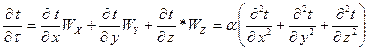где 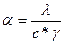- коэффициент температуропроводности, м²/ч.

Эти уравнения математически описывают сложный процесс теплоотдачи, но для большинства случаев, встречающихся на практике, они не разрешимы и по ним нельзя определить . Поэтому применяют теорию подобия, которая позволяет решить эти уравнения в критериальной форме.

Выведем основные критерии теплового подобия:

1) критерий Рейнольдса (от него зависит теплообмен в движущейся среде),

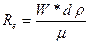
2) критерий Нуссельта

а) возьмём дифф. уравнение, характеризующее условия на границе:

;

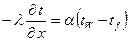б) разделим на левую часть:

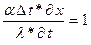
где 1 – безразмерный комплекс;

в) сократим знаки дифф. и одноимённые величины.

,

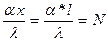N – характеризует условия на границе, интенсивность теплообмена на границе раздела фаз.

3) критерий Фурье

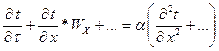
делим на

Характерная связь между скоростью изменения температурного поля, размерами и физическими характеристиками в нестационарном процессе.

4) критерий Пекля.

делим 2-ой член на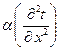

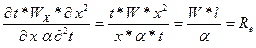
R_e – характеризует отношение тепла, передав. конвек. и теплопроводность. Критерий обычно представляют в виде произведений критериев R_e и P_r.

,

где ;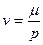

характеризует поле теплофизических величин

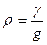
В случаях, когда теплообмен происходит в результате естественной конвекции, обусловленный разностью плотностей жидкости в различных точках системы, процесс характеризуется критерием Архимеда

где 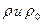- плотности холодной и нагретой жидкости.

Из критерия Архимеда получается критерий Грасгоффа, путём замены 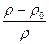на 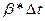, т.к. - определяет разности температур в точках системы

.

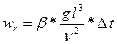Таким образом, в общем виде критериальное уравнение для конвективного теплообмена будет иметь вид:

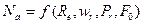
Опытные данные по конвективному теплообмену

Для расчётов в процессах теплоотдачи надо уметь пользоваться опытными данными, т.е. произвести выбор тех данных, которые соответствуют конкретному случаю теплоотдачи. Это важно, т.к. опытных данных по конвективному теплообмену очень много и они позволяют рассчитать для всех основных случаев теплообмена.

Свободное движение жидкости

Свободное движение жидкости происходит за счёт разности плотностей нагретых и холодных частей, а это зависит от разности температур твёрдого и жидкого тела. Следовательно, одним из определяющих критериев должен быть критерий Грасгоффа. С другой стороны также зависит и от теплофизических параметров жидкости, т.е. в критериальном уравнении должен быть критерий Прандтля (P_r). Опытные данные обрабатывают по уравнению:

,

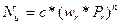где с и n – постоянные величины, получаемые опытным путём.

Имеются таблицы значений этих величин в зависимости от произведения (w_r * P_r)

Теплоотдача при вынужденном движении жидкости

Очевидно, не может вызывать сомнения, что интенсивность теплоотдачи при вынужденном движении жидкости зависит от характера этого движения и следует различать три вида этого движения:

1) установившийся турбулентный режим, R_e > 10000;

2) переходный режим 2300 < R_e <10000;

3) ламинарный режим R_e < 2300.

Поэтому для каждого режима (а в каждом режиме, как правило, есть ещё и частные случаи) имеются свои, полученные опытным путём, критериальные уравнения.

Изменение состояния в химической технологии в большом количестве процессов теплоотдачи сопровождается изменением агрегатного состояния. Поэтому на этом случае теплоотдачи стоит остановиться подробнее. Особенности таких процессов теплообмена заключается в том, что тепло подводится к материалам и отводиться от них при постоянной температуре и распространяется не в одной, а в двух фазах. Эти особенности передачи тепла, следовательно, должны быть учтены.

Рассмотрим процесс теплообмена при конденсации пара.

dQ

W dF x

, [ ккал/час ]

С другой стороны это же количество тепла отводится от поверхности теплопроводностью и можно записать:

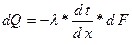, [ ккал/час ]

тогда

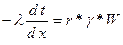
или

.

Заменив в последнем выражении , получим:

.

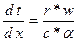Преобразуем последнее выражение методом подобия и получим:

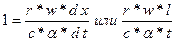
Полученный критерий представляют в виде произведения двух критериев, причём температуру заменяют некоторой разницей температур, т.е.

,

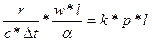где k – критерий теплового подобия при изменении агрегатного состояния;

- разность между температурой фазового перехода и температуры одной из фаз;

с *- теплота перегрева или переохлаждения рассматриваемой зоны относительно температуры фазового превращения.

Из различных случаев теплоотдачи при изменении агрегатного состояния наибольшее значение для процессов химической технологии имеет теплоотдача при конденсации паров и теплоотдача при кипении жидкости.

В тепловых процессах осуществляется передача тепла – теплопередача от одного теплоносителя к другому.

Тепловое излучение

По своей физической сущности тепловое излучение совершенно аналогично излучению света и отличается только длиной волны 0,8 – 40 мк.

Энергия излучения Е (в единицу времени и с единицы поверхности) зависит от длины волны и от температуры. Для абсолютно чёрного тела эту зависимость даёт теоретическое уравнение Планка:

,

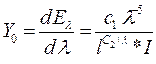где С₁ и С₂ – универсальные постоянные (С ₁ = 3,17*10^-16 ккал*м²/час; С₂ = 0,0143 м*град).

Характер зависимости представляет изотерму с максимумом, и чем выше температура тела, тем максимум больше сдвинут в область коротких волн.

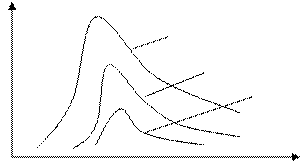Y₀

1200⁰

1000⁰

800⁰

Можно записать:

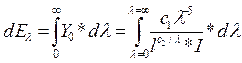
Интегрирование этого выражения даёт зависимость лучеиспускательной способности абсолютно чёрного тела.

Закон Стефана – Больцмана:

E₀ = k₀*T^U,

где k₀ = 4,9*10^-8 ккал/м²*час*⁰К

Для большего удобства при технических расчётах эту зависимость применяют в следующем виде:

,

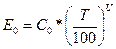где С₀ = 4,9 ккал/м²*час*⁰К – коэффициент излучения абсолютно чёрного тела.

Опытные работы Стефана и других учёных показали, что этот закон применим не только к абсолютно чёрным телам, но и к серым телам и записывается в следующем виде:

,

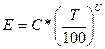где С [ ккал/м²*час*⁰К ] – коэффициент излучения серых тел (всегда меньше С₀ и изменяется от 0 до 4,9).

Отношение - называется степенью черноты тела и тогда закон изменения серых тел выражается так:

.

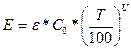Закон Кирхгофа.

Он устанавливает соотношение между лучеиспускательным и поглощательными способностями тел, это соотношение можно получить из рассмотрения процесса обмена лучистой энергии между абсолютно чёрным и серым телом.

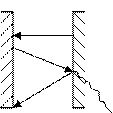
Т₀ Е Т

Е₀ Е₀ Е

А₀ А

Е₀(1-А) Е₀А

T > T₀, тогда абсолютно чёрное тело суммарно получает энергии:

q = E+E₀ (1 - A) – E₀ =E-T₀*A,

а если Т = Т₀, тогда q = 0, и Е = Е₀*А или

Е₀ = Е/А,

т.е. отношение лучеиспускательной способности к поглощательной для всех тел одинаково и равно лучеиспускательной способности абсолютно чёрного тела и зависит только от температуры. В практике больше всего приходится рассчитывать теплообмен между телами.

Количество тепла q рассчитывают по уравнению:

,

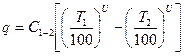где С_1-2 - приведённый коэффициент лучеиспускательной способности тел, ккал/м²*час*⁰К,

при чём это уравнение легко выводится из теплового баланса тел.

Лучеиспускательной способностью обладают некоторые газы (водяной пар, аммиак, углекислота и сернистый газ). Уравнение для расчёта количества тепла переданного газом за счёт лучеиспускания подобно выше приведённому примеру.

(*)

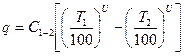Практически лучистый теплообмен всегда сопровождается конвективным теплообменом, поэтому приведем уравнение (*) к другому виду.

Для этого умножим и разделим уравнение на (t₁ – t₂) и получим:

,

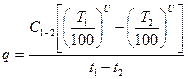обозначим последнее выражение 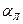, тогда

,

где 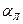- коэффициент теплоотдачи лучеиспускания .

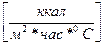Определение поверхности нагрева

Расчёт теплообменной аппаратуры, как правило, сводится к расчёту поверхностей теплопередачи. Поверхность теплопередачи определяют по основному уравнению теплопередачи:

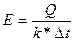
Количества тепла определяют по уравнениям теплового баланса.

Массообменные прцессы

Дата добавления: 2014-01-04