Ток в вакууме

Как известно, в металлах' имеются электроны проводимости, образующие "электронный газ" и участвующие в тепловом движении. Для того, чтобы свободный электрон мог выйти из металла, должна быть совершена определенная работа, различная для разных металлов и названная работой выхода.

Существование работы выхода показывает, что в поверхностном слое металла существует электрическое поле, значит, электрический потенциал при переходе через этот слой изменяется на некоторую величину, также специфичную для разных металлов. Эта поверхностная разность потенциалов связана с работой выхода соотношением: A=ef

При наличии электрического поля ион обретает такую скорость установившегося движения, при которой сила трения и сила еЕ со стороны

поля

Отсюда получаем, что

v=bE.

Через b обозначена подвижность иона. Вообще говоря, подвижность анионов и катионов различна, поэтому вводят обозначения Ь+ Ь_ Число переноса катионов

р,= ЬДЬ++Ь_).

Электрический ток в газах.

В обычном состоянии газы не проводят электричества. Однако под влиянием

различных внешних факторов (высокая температура, различные излучения) газы становятся электропроводящими. Это происходит вследствие того, что от нейтральных атомов отделяются электроны и образуются проводящие частицы - положительные ионы и свободные электроны. Часть свободных электронов может быть захвачена нейтральными атомами и образуются отрицательные ионы. Эт&т процесс называется ионизацией. Ионизация атома (отрыв электрона) требует определенной энергии, величина которой зависит от строения атома и называется энергией ионизации.

Если ионизацию не поддерживать, например, бомбардируя атомы электронами, ускоренными во внешнем электрическом поле, то со временем происходит рекомбинация ионов - положительный и отрицательный ион в результате теплового движения сталкиваются и избыточный электрон переходит к положительному иону. В результате образуется два нейтральных атома. Рассмотрим принципиальную схему, изображенную на рисунке:

Электрический ток в металлах — это упорядоченное движение электронов под действием электрического поля.

Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов (опыт Толмена и Стьюарта):

Рис. 9.1

Катушка с большим числом витков тонкой проволоки (рис. 9.1) приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру.Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся гальванометром.

При торможении вращающейся катушки на каждый носитель заряда е массой т действует тормозящая сила, которая играет роль сторонней силы, то есть силы неэлектрического происхождения:

и-

г =-w—

6t

Сторонняя сила, отнесенная к единице заряда, по определению является

Б

напряженностью «поля сторонних сил:

du £ di

Следовательно, в цепи при торможении катушки возникает электродвижущая сила:

E-V—' в dt

За время торможения катушки по цепи протечет заряд q, равный

где - длина проволоки катушки, / - мгновенное значение силы тока в

катушке, R - полное сопротивление цепи, ^ - начальная линейная скорость проволоки.

Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема.

Предположение о том, что за электрический ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 году немецкий ученый П. Друде на основе гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика X. Лоренца и носит название классической электронной теории. Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ.

Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла. Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер. Высота этого барьера называется работой выхода.

При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера. Согласно теории Друде-Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость теплового движения электронов по формулам молекулярно­кинетической теории: ^{Urm =} ^ *^^с

При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток. Величина дрейфовой скорости электронов лежит в пределах 0,6 — 6 мм/с. Таким образом, средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения.

Малая скорость дрейфа не противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью с Щ 3-10 м/с. Через время г=//с (/ - длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.

В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.

Несмотря на то, что все эти допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках: закон Ома, закон Джоуля - Ленца и объясняет существование электрического сопротивления металлов.

Закон Ома:

1 e*vtS e*vtS

1 = «tfftL = | LJZfLu

2 m 2mi Электрическое сопротивление проводника:

в htS

Закон Джоуля—Ленца:

_а «As».*» £/*. до ------ в² ----------------- ULi =—А/

т 2т 2т R

Однако в ряде вопросов классическая электронная теория приводит к выводам, находящимся в противоречии с опьггом. Эта теория не может, например, объяснить, почему молярная теплоемкость металлов, также как и молярная теплоемкость диэлектрических кристаллов, равна 3R (закон Дюлонга и Пти). Классическая электронная теория не может также объяснить температурную зависимость удельного сопротивления металлов:

теория дает ^ ~ ^, в то время как из эксперимента получается зависимость р~Г.

Наиболее ярким примером расхождения теории и опытов является сверхпроводимость.

Зонная модель электронной проводимости металлов

Качественное различие между металлами и полупроводниками (диэлектриками) состоит в характере зависимости удельной проводимости от температуры. У металлов с ростом температуры проводимость падает, а у полупроводников и диэлектриков растет. При Т ® О К у чистых металлов проводимость s®¥. У полупроводников и диэлектриков при Т ® О К, s ® 0. Качественного различия между полупроводниками и диэлектриками в отношении электропроводности, нет.

Проявление у одних веществ металлических свойств, а у других полупроводниковых и диэлектрических может быть последовательно объяснено только в рамках квантовой теории.

Согласно квантовым представлениям, энергия электронов в атоме может изменяться дискретным образом. Причем, согласно принципу Паули, в одном квантовом состоянии может находиться не более одного электрона. В результате электроны не собираются на каком-то одном энергетическом уровне, а последовательно заполняют разрешенные энергетические уровни в атоме, формируя его электронные оболочки.

При сближении большого числа атомов и образовании кристаллической структуры химические связи между атомами образуются за счет электронов, находящихся во внешних, валентных, электронных оболочках.

Согласно принципу Паули, атомы не могут сбиться в плотную массу, поскольку в этом случае в одном квантовом состоянии оказалось бы много частиц с полуцелым спином - собственный моментам количества движения (L = h/2). Такие частицы называются ферчионами, и к ним, в частности, относятся электроны, протоны, нейтроны. Названы они так в честь итальянского физика Э. Ферми, впервые описавшего особенности поведения коллективов таких частиц. При сближении большого числа атомов в пределах твердого тела происходит расщепление исходного энергетического уровня валентного электрона в атоме на N подуровней, где N - число атомов, образующих кристалл. В результате образуется зона разрешенных энергетических уровней для электронов в твердом теле (рис.9.2).

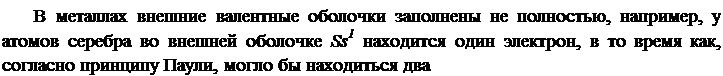электрона с различными ориентациями спинов, но второго электрона во внешней оболочке атома серебра просто нет. При сближении N атомов Ag и расщеплении внешнего энергетического уровня 5s¹1 на N подуровней каждый из них заполняется уже двумя электронами с различными ориентациями спинов. В результате при сближении N атомов серебра возникает энергетическая зона, наполовину заполненная электронами. Энергия, соответствующая последнему заполненному электронному уровню при О К, называется энергией Ферми ерШШк Расстояние между соседними энергетическими уровнями 1|| очень мало, поскольку N очень велико, до 10^й см-⁵.

ер~ 1,10 эВ, АЕ = e_F/N «кТ» 0,025 эВ.

Расстояние между соседними разрешенными уровнями электронов в металлах много меньше энергии теплового движения электронов даже при самых низких температурах. Если поместить проводник в электрическое поле, включив его, например, в замкнутую цепь с источником ЭДС, то электроны начнут перемещаться из точки проводника с меньшим потенциалом к точке с большим потенциалом, так как их заряд отрицателен. Но движение в электрическом поле означает увеличение энергии электрона, а по квантовым представлениям, переход на более высокий энергетический уровень у электрона возможен, если этот соседний уровень свободен. В металлах таких свободных уровней для электронов, находящихся вблизи уровня Ферми, вполне достаточно, поэтому металлы являются хорошими проводниками электрического тока.

Однако эту проводимость обеспечивают не все свободные электроны металла, а лишь те из них, что расположены вблизи уровня Ферми. Концентрация таких электронов примерно равна nT/T_g, где T_g = 5*10 К — температура вырождения.

Глава 20 ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ, ГАЗАХ И ПЛАЗМЕ

20.1. Законы Фарадея для электролиза

1. Неметаллические проводящие жидкости обладают ионной проводимостью, т.е. но­сители тока в них — положительно и отрицательно заряженные ионы. Такие жидкости называются электролитами, или проводниками II рода. Типичными примерами элект­ролитов могут служить водные растворы солей, кислот и щелочей.

Упорядоченное движение ионов в проводящих жидкостях происходит в электричес­ком поле, которое создается электродами — проводниками, опущенными в электролит и соединенными с полюсами источника электрической энергии. Положительный электрод называется анодом, отрицательный — катодом. Положительные ионы (ионы водорода и металлов) движутся к катоду и потому называются катионами, а отрицательные ионы (ионы кислотных остатков и гидроксильной группы) движутся к аноду и называются ани­онами. Электрический ток в электролитах сопровождается явлением электролиза — вы­делением на электродах составных частей растворенных веществ или других веществ, яв­ляющихся результатом вторичных реакций на электродах.

2. Основные законы электролиза были экспериментально установлены М. Фарадеем (1834).

Первый закон Фарадея:

масса т выделившегося на электроде вещества пропорциональна электрическому за­ряду Q, прошедшему через электролит:

тп = kQ. (20.1)

Коэффициент пропорциональности А: называется электрохимическим эквивалентом вещества. Он численно равен массе вещества, выделяющегося при прохождении через электролит единичного электрического заряда, и зависит от химической природы веще­ства.

Второй закон Фарадея:

электрохимические эквиваленты различных веществ относятся, как их химические эк­виваленты Jfc*:

h.-b.2, (20.2)

Химическим эквивалентом иона называется отношение молярной массы Миона к его валентности Z: Л* = M/Z. Поэтому электрохимический эквивалент

* = “. (20.3)

где F— универсальная постоянная, названная постоянной Фарадея. Подставим выраже­ние (20.3) в (20.1), получим

1 М _л

m = (20.4)

Формула (20.4) объединяет в себе оба закона Фарадея, т. с. является записью объеди­ненного закона Фарадея для электролиза.

Если через электролит пропускается в течение времени (постоянный электрический ток /, то заряд Q ш It и уравнение (20.4) можно записать в виде

m^ltLlt. (20.4')

г Z

Из объединенного закона Фарадея (20.4) легко понять физический смысл постоян­ной Фарадея. Если т = М/Z, то заряд Q_t прошедший через электролит, равен постоянной Фарадея. Следовательно, постоянная Фарадея численно равна электрическому заряду, при прохождении которого через электролит на электроде выделяется 1 моль одновален­тного вещества.

3. Законы Фарадея впервые навели на мысль о том, что любой электрический заряд состоит из целого числа «атомов электричества* — элементарных зарядов. Действитель­но, из (20.4) следует, что для выделения на электроде 1 моля любого ^-валентного веще­ства требуется пропустить через электролит заряд Q = ZF. Этот заряд переносится в элек­тролите одним и тем же числом ^-валентных ионов, равным постоянной Авогадро JV_A. Возможны два различных истолкования такой закономерности:

а) заряды Zr валентных ионов различны, но в среднем равны ZF/N_А, подобно тому, как в газе молекулы обладают различной кинетической энергией поступательного движения, но в среднем она равна */%!&)

б) каждый ион несет вполне определенный заряд q = ZF/N_А, причем заряды ионов могут отличаться лишь на величины, кратные элементарному заряду одновалентного иона e=F/N_K.

С помощью специально поставленных опытов была доказана правильность второго утверждения, а также экспериментально найдено значение элементарного заряда е.

4. Схема опытов, проведенных А. Ф. Иоффе (1912), показана на рис. 20.1.

Опыт. Отрицательно заряженная металлическая пылинка помещалась между обкладками кон­денсатора, напряженность поля в котором подбиралась такой, чтобы пылинка находилась в равно­весии. Затем пылинка освещалась ультрафиолетовым светом малой интенсивности. Вследствие фотоэффекта отрицательный заряд пылинки время от времени уменьшался и для сохранения рав­новесия пылинки приходилось так изменять напряженность электрического поля в конденсаторе, чтобы электрическая сила qE не изменялась: — ••• •

Опыты показали, что заряд пылинки может принимать лишь ряд дискретных значений.

5. Элементарный электрический заряд был измерен Р. Милликеном (1909—1914).

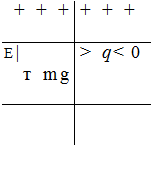Опыт. Идея опытов Милликена состояла в определении заряда микроскопической масляной капли сферической формы на основе измерения скорости ее установившегося движения в однород­ном электрическом поле плоского конденсатора. Пластины конденсатора были расположены гори­зонтально, как и в опытах А. Ф. Иоффе. В отсутствие электрического поля капля равномерно падала вертикально вниз под действием трех взаимно уравновешивающихся сил: силы тяжести mg капли, архимедовой силы F_apx и силы сопротивления воздуха F_C0lip. Как показал Д. Стокс, сила сопротивления, действующая на твердый шар при его медлен­ном поступательном движении со скоростью v в вязкой жилкой или газообраз­ной среде, равна

Рсоир = -6ит)пг, (20.5)

где г — радиус шара; т) — динамическая вязкость среды.

Пусть ц, — скорость установившегося падения капли в отсутствие элект- рического поля, тогда

7э(р - Р.)тtr³g «бицпь, (20.6)

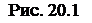где р и р, - плотности масляной капли и воздуха в конденсаторе. Измерив и зная плотности р и р„, а также tj, можно было найти из (20.6) радиус капли:

Г = З-у/лМ^Р - P»)g]‘

Зная направление Б, можно было определить и знак заряда капли. Если при постоянном значе­нии напряженности поля Е слегка изменить заряд капли на Д q, то соответственно изменится на At>j и скорость ее установившегося подъема вверх, причем, согласно (20.8),

(20.9)

В опытах Милликена заряд капли можно было изменять путем слабой ионизации воздуха рент­геновским излучением. Опыты показали[1], что и q, и Aq кратны одному и тому же элементарному заряду е. Соответственно постоянная Фарадея равна F = еЛ'_А.

20.2. Закон Ома для плотности тока в электролитах

1. Опыты показали, что закон Джоуля — Ленца (19.14) справедлив для электрическо­го тока не только в металлических проводниках, но также и в электролитах. Отсюда сле­дует, что диссоциация молекул электролита на ноны не связана с прохождением электри­ческого тока и затратой на нее энергии тока. Диссоциация молекулы соли, кислоты или щелочи, состоящей из взаимосвязанных ионов, происходит в растворе при ее столкнове­ниях с другой молекулой растворенного вещества или растворителя, имеющей достаточ­но большую кинетическую энергию теплового движения. Интенсивная диссоциация со­лей, кислот и щелочей в водных растворах объясняется тем. что молекулы воды обладают большим электрическим моментом, т.е. подобны сильно вытянутым диполям. Под влия-

нием электрического поля полярной молекулы соли (кислоты, щелочи) окружающие ее молекулы воды ориентируются преиму­щественно так (рис. 20.2), что своим электрическим полем су­щественно ослабляют связь между ионами в молекуле раство­ренного вещества и тем самым облегчают ее диссоциацию.

2. Из-за хаотического теплового движения ионов в растворе происходит и обратный процесс столкновения ионов противопо­ложных знаков и воссоединения их в нейтральные молекулы. Этот процесс называется молизацией или рекомбинацией. Пусть По — концентрация молекул растворенного вещества, из которых а»% диссоциированы на ионы, где а — коэффициент диссоциации. Очевидно, что число молекул А«$, которые диссоциируют за еди-

ицу времени в единице объема раствора, пропорционально числу недиссоциированных молекул в этом объеме:

Дпо = 0(1 — а)яо,

где 3 — коэффициент пропорциональности.

Число Л по нейтральных молекул, образующихся в единице объема раствора за едини­цу времени в результате процесса рекомбинации, пропорционально как числу положи­тельных ионов, так и числу отрицательных ионов, содержащихся в единице объема:

Дп'о = ча²71„²,

где "j — коэффициент пропорциональности.

В состоянии динамического равновесия Длб = Дпо, т.е. (3(1 — а)п<, = 'уа²я|о или

(1 — а)/а² = const • щ. (20.10)

Если пц —» 0, то а —» 1, т. е. в слабых растворах почти все молекулы диссоциированы (а ««1). По мере увеличения концентрации щ раствора коэффициент диссоциации отбыва­ет. В сильно концентрированных растворах а ~

3. Плотность j электрического тока в электролите равна геометрической сумме плот­ностей тока положительных и отрицательных ионов: j =j₊ 4- j_, причем

j₊ = q+no+(v+), j. = g_no_(v_>, (20.11)

где q+ и и По_, (v₊) и (v_) — заряды, концентрации и средние скорости упорядочен­

ного движения (дрейфа) положительных и отрицательных ионов в электрическом поле. Аналогично тому, как скорость дрейфа электронов проводимости в металле пропорцио­нальна напряженности Е электрического поля, скорости дрейфа ионов также пропорцио­нальны Е:

(v+> = И+Е, СО = -Ц-Е, (20.12)

где и — положительные величины, называемые подвижностями ионов. Как показы­вают опыты, подвижность иона зависит от его природы, а также от температуры, вязкости и других характеристик электролита. Существенно, что подвижность ионов в электроли­тах не зависит от напряженности Е электрического поля.

Соотношения (20.12) можно получить, рассматривая дрейф ионов как их установив­шееся движение в вязкой среде — электролите с постоянными скоростями (v₊) и (v_). При этом для каждого иона электрическая сила уравновешивается силой вязкостного сопротивления электролита, которая пропорциональна скорости дрейфа иона. Например, для положительного иона g₊ Е 4- F+ = 0, где сила сопротивления F+ = — c+(v+), а с+ — положительный коэффициент пропорциональности, так что (v₊) = щ.Е, где = <7+/^с+-

4. С помощью выражений (20.12) плотность тока в электролите можно представить в форме

j = (я+щ+\1₊ - g_no-4i-)E. (20.13)

В электролитах, так же как в металлических проводниках, нет объемных зарядов. По­этому q+T*b+ + g_no- = 0 и

j «9+Ло+(щ. + И-)^Е- (20.13')

Образование ионов в электролите не связано с прохождением электрического тока. Поэтому их концентрации По+ и подобно подвижностям и ц_, не зависят от напря­женности электрического поля. Таким образом, формулы (20.13) и (20.13') показывают, что для плотности тока в электролитах выполняется закон Ома:

плотность тока в электролите пропорциональна напряженности электрического поля и совпадает с ней по направлению.

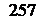9 Дсшф

5. Заряд положительного иоиа равен произведению элементарного заряда е на вале! тность иона Z₊: q+ — eZ₊. Поэтому закон Ома (20.13') для плотности тока в электролитах можно записать в виде

j jj e2₊n₀₊(|x₊ + м-)Е = Е/р. (20.14)

Удельное электрическое сопротивление электролита

р = [ег₊щ₊(\1₊ + ц_)]^-1. (20.15)

Концентрация положительных ионов зависит от концентрации щ молекул электро­лита, коэффициента диссоциации Ц и числа Ц положительных ионов, образующихся при диссоциации одной молекулы: g = k+ariQ. Следовательно,

р = [eZ+k+ariQ^ + р_)]^-1 (20.15^х)

или

р = + ц_)]^-1, (20.16)

где С= k+Z+rio/Nb — эквивалентная концентрация электролита.

С повышением температуры раствора электролита его удельное электрическое сопро­тивление р уменьшается, так как, во-первых, увеличивается коэффициент диссоциации

а, во-вторых, уменьшается вязкость раствора и соответственно возрастают подвижности ионов Щ и |л_. Зависимость р от концентрации раствора имеет сложный характер, так как при изменении концентрации изменяются также коэффициент диссоциации и подвиж­ности ионов. При малых концентрациях а и (р,₊ + р_) изменяются мало, так что р убывает обратно пропорционально С. При дальнейшем увеличении концентрации р достигает ми­нимума, а затем возрастает вследствие снижения как коэффициента диссоциации а, так и подвижностей ионов.

Как показывают опыты, ионной проводимостью обладают не только водные растворы солей, кислот и щелочей, но и, например, расплавленные соли. Это явление широко ис­пользуется в электрометаллургии для получения алюминия, магния и ряда других ме­таллов.

20.3. Электрическая проводимость газов

1. Газы в отличие от металлов и электролитов состоят из электрически нейтральных атомов и молекул, т. е. не содержат свободных заряженных частиц — носителей тока, спо­собных приходить в упорядоченное движение под действием электрического поля. Сле­довательно, при обычных условиях газы не проводят электрический ток. Газ становится проводником, если часть его молекул ионизировать, т.е. расщепить на свободные элект­роны и положительные ионы. В газе могут образовываться и отрицательные ионы вслед­ствие присоединения части освободившихся электронов к нейтральным молекулам газа.

Атомы и молекулы — устойчивые системы заряженных частиц. Поэтому для иониза­ции атома (или молекулы) газа необходимо совершить работу ионизации А„. Работа иони­зации зависит от химической природы газа и энергетического состояния вырываемого электрона в ионизируемом атоме или молекуле. Наиболее слабо связаны в атоме внешние (валентные) электроны. Поэтому для удаления из атома валентного электрона нужно за­тратить меньшую работу, чем для вырывания любого другого электрона атома. После уда­ления из атома валентного электрона и образования таким образом положительного иона прочность связи остальных электронов возрастает. Следовательно, для удаления из од­нократно ионизированного атома (одновалентного иона) еще одного электрона нужно совершить работу, которая значительно больше работы отрыва первого электрона. Так, например, работа ионизации атома азота (N) равна 14,5 эВ, а его одновалентного иона (iV⁺) — 29,6 эВ, двухвалентного иоиа (N⁺⁺) — 47,4 эВ и т.д.

зар«.«»«о

Сооггветствет»^

тс ^£ да

“ " ^{П13ации можио} характеризовать с помощью потенциала ионизации.

ионизации _у', называется разность потенциалов, которую должен прой-

ти элопрон в ускоряющем электрическом поле, чтобы увеличение его энергии было рав- но роюотс иоимззщнн.

Из (13.25) следует, что

«ь = k«/e. (20.17)

Значения потенциалов ионизации некоторых атомов и молекул приведены в табл. 20.1.

Таблица 20.1

Атомы | Н 1 \--- 1 1	Не		V 1	Ne	Cl ^1	Na	Hg	К	Аг
	13.6	24,6	13.6	143 1	21.6	13,0	5,14	10,4		15$
1 Молекулы	H ^2	о,	н2о	N,	NO,	Cl2	СО,	СО	НС1	NO
;..В 1....	15,4	12_2	1 12.6 1	15.6			13,8	14,0	12.6	9,2

3. Ионизация газа может происходить под влиянием различных внешних воздействий — сильного нахрева газа, рентгеновского излучения, гамма-излучения, бомбардировки мо­лекул газа быстро движущимися электронами, ионами, нейтронами и другими частица­ми. Количественной характеристикой процесса ионизации служит интенсивность иони­зации, равная числу пар противоположных по знаку заряженных частиц, возникающих в единице объема газа за единицу времени.

В обычных условиях газ подвергается действию космического и радиоактивного из­лучений- Поэтому, строго говоря, проводимость газа никогда не равна нулю: в нем всегда имеются свободные заряженные частицы, если только не приняты специальные меры за­щиты газа от д ействия всех естественных внешних ионизаторов. Однако интенсивность ионизации под влиянием космических лучей и распада рассеянных в земной коре радио­активных элементов очень мала. Поэтому проводимость газов в естественных условиях хотя и ае равна нулю, но очень мала. В дальнейшем показано, что присутствие в газах даже малого количества свободных электронов и ионов играет существенную роль в воэ- никиовении заметной проводимости газов в достаточно сильных электрических полях.

4. Рассмотрим подробнее процесс ионизации газа под действием быстро движущихся электронов, ионов и других частиц, получивший название ударно! ионизации- Для про­стоты будем считать, что газ — одноатомный- При столкновении частицы с нейтральным атомом газа она передает ему часть своей энергии. Если кинетическая энергия частицы сравнительно мала, то» как показывают опыты, се соударение с атомом является уярупш. Энергия, сообщаемая атому в этом случае, недостаточна для его ионизации. Бомбарди­ровка атомов газа такими частицами вызывает лишь нагревание газа.

Совершенно иначе происходят соударения с атомами газа частиц, кинетическая энер­гия которых достаточно велика. В этом случае, как показывают опыты, соударения ста­новятся неупрутми и вызывают возбуждение атомов газа, т е перевод атома из нор­мального энергетического состояния в состояние с повышенной энерпгей, иди даже иони­зацию атома. Оценим минимальное значение кинетической энергии, которой должна обладать частица для того, чтобы вызвать ударную ионизацию атома газа. Скорость теп­лового движения молекул во много раз меньше скорости ионизирующей частицы. По» этому можно считать, что до удара атом неподвижен. Полагая, что скорость ▼ ионизиру­ющей частицы во много раз меньше скорости света в вакууме, а масса частицы рвана т, м применяя закон сохранения импульса при ису прутом ударе (12) к столкновению ча­стицы с атомом. получим

Щ_________ _ скорость частицы и атома после удара. При этом приближенно

считается, что скорость электрона, выбитого и.< атома, тоже равна и. Начальная кинети­ческая энергия частицы расходуется при ударе на работу ионизации А„ и сообщение ато­му и частице кинетической энергии, соответствующей их скорости и после уда

Лпиг ш А_ы + /з(^т + АО***-

(20.19)

		т At)
		А и 1			(20 20)

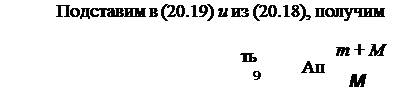Таким образом, минимальная кинетическая энергия, которой должна обладать части­ца для осуществления ударной ионизации атома газа, не может быть меньше работы иони­зации А_н и будет тем ближе к А_н, чем меньше масса частицы по сравнению с массой атома. Для электрона эта энергия меньше, чем для любого иона. В одном и том же ускоряющем электрическом поле электрон и одновалентный ион приобретают одинаковую кинетичес­кую энергию W_K — еД(р. Поэтому для осуществления ударной ионизации ионы должны пройти в ускоряющем электрическом поле большую разность потенциалов, чем электро­ны. Работа, необходимая для возбуждения атома, меньше работы ионизации. Следова­тельно, неупругие столкновения частиц с атомами газа возможны и при энергии частиц, меньшей значения, получаемого по формуле (20.20).

Процесс столкновения частицы с молекулой, состоящей из двух или большего числа атомов, качественно подобен рассмотренному для одноатомного газа. Однако следует иметь в виду, что возбуждение двухатомной и более сложной молекулы может состоять в

увеличении энергии не только ее электронов, но также вра­щательного и колебательного движений молекулы.

5. Одновременно с ионизацией газа в его объеме про­исходит и обратный процесс рекомбинации ионов и элек­тронов в нейтральные частицы — атомы и молекулы.

Рассмотрим опыт, иллюстрирующий процесс реком­бинации (рис. 20.3).

Опыт. В стеклянный сосуд А, расширяющийся вниз, впая­ны электроды В, Си D, соединенные с одинаковыми электроско­пами. Электроскопы заряжают так, чтобы их листочки разошлись на одинаковые углы (рис. 20.3, а). Затем под сосуд А подводится газовая горелка, в пламени которой воздух ионизируется. Струя горячего ионизированного воздуха поднимается в цилиндре А вверх. При этом листочки электроскопа Ь быстро спадают, листоч­ки электроскопа с спадают значительно медленнее, а отклонение листочков электроскопа d вообще не изменяется (рис. 20.3,6). Из опыта следует, что в течение време­ни. необходимого для подъема ионов до уровня электродов до Си Д происходит постеленное умень­шение электрической проводимости нагретого воздуха, обусловленное процессом рекомбинации.

20.4. Несамостоятельный газовый разряд

1. Прохождение электрического тока через»газ называется электрическим разрядом в газе или газовым разрядом.

Если электропроводность газа создается и поддерживается за счет действия внешнего источника ионизации, то происходящий при этом электрический разряд в газе называет­ся несамостоятельным.газовым разрядом. Несамостоятельный газовый разряд прекра­щается, как только прекращается действие внешнего ионизатора.

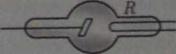
На рис. 20.4 показана схема установки для изучения вольт-амперной характеристики (ВАХ) несамостоятельного газового разряда в заполненной газом стеклянной трубке М, т.е. зависимости силы тока / от напряжения (разности потенциалов) Uмежду электрода­ми А и К, впаянными в трубку. Напряжение регулируется потенциометром Р и измеряет­ся вольтметром V. Для измерения силы тока / служит чувствительный гальванометр G. Газ ионизируется рентгеновским излучением, испускаемым рентгеновской трубкой R (электрическая цепь питания этой трубки на рисунке не показана). Интенсивность иони­зации газа в трубке М не изменяется во время опыта.

2. Результаты измерений представлены на графике, изображенном на рис. 20.5. При небольших значениях напряжения [/сила тока /пропорциональна U(область 1). Эго легко понять, если учесть, что несамостоятельный газовый разряд подобен току в электроли­тах: оба они осуществляются упорядоченно движущимися ионами (свободные электро­ны в ионизованном газе можно рассматривать как простейшие отрицательные ионы). Следовательно, в данном случае для плотности тока j в разряде можно воспользоваться выражением (20.13')- При ионизации газа обычно образуются электроны и одновалент­ные положительные ионы. Поэтому можно принять, что д₊ = е и = л<> где щ — число пар ионов в единице объема газа. Тогда, согласно (20.13'),

j = епо(Ш- + 1*-)Е

Как показывает опыт, подвижности газовых ионов в широком интервале давлений обратно пропорциональны давлению и при не слишком больших значениях напряженно­сти поля Б не зависят от Е. Таким образом, при небольших значениях Е несамостоятель­ный разряд в газе подчиняется закону Ома.

3. При дальнейшем увеличении напряжения U между электродами линейная зависи­мость силы тока /от {/нарушается (область2) - сила тока растет медленнее, чем U. Эта закономерность связана со следующим существенным отличием несамостоятельного га­зового разряда от тока в электролитах — убыль ионов, участвующих в проводимости элек­тролита и нейтрализующихся у электродов, непрерывно пополняется в объеме электро­лита за счет диссоциации новых молекул. Поэтому число по пар ионов в единице объема электролита в первом приближении не зависит от плотности тока и остается постоян­ным. В несамостоятельном газовом разряде пополнение ионов в газе целиком зависит от мощности внешнего источника ионизации. Поэтому можно считать, что Цд=const и j про­порционально Е (соответственно / пропорционально U) только при малых значениях плотности и силы тока, т.е. при малых значениях Е и U. При дальнейшем увеличении Е концентрация ионов убывает, что приводит к нарушению закона Ома в области 2.

К

/4

©

U

Ж

р *

Ш1й

Рис 20.4

ДО

4. Начиная с некоторого значения напряжения U„ сила тока ири несамостоятельном pari) ряде остается неизменной, несмотря на дальнейшее увеличение напряжения (область 3). Это явление объясняется тем, что все ионы, возникающие в газе, ие успевают на пути к электродам воссоединяться в нейтральные молекулы: все они доходят до электродов. Сила тока газового разряда достигает наибольшего значения, возможного при данной интен­сивности ионизации, определяющейся внешним ее источником. Этот ток называется то­ком насыщения /„. Если Пе_0К — число пар одновалентных ионов, образующихся в газе за 1 с иод действием внешнего ионизатора, то ток насыщения равен

/„ = еп_сск. (20.22)

При дальнейшем увеличении напряжения между электродами сила тока начинает резко возрастать (область 4). Это явление, обусловленное возникновением ударной ионизации газа и резким возрастанием числа свободных носителей заряда, рассматривается в 20.5.

20.5. Самостоятельный газовый разряд

1. Электрический разряд в газе, сохраняющийся после прекращения действия внеш­него ионизатора, называется самостоятельным газовым разрядом.

Для его осуществления необходимо, чтобы в результате самого разряда в газе непре­рывно образовывались носители тока. Основным источником их возникновения являет­ся ударная ионизация молекул газа.

Рассмотрим влияние напряжения между электродами газоразрядной трубки М (см. рис. 20.4) на проводимость газа и процессы, происходящие в нем при разряде. Если на­пряжение Uдостаточно велико, то электроны, возникающие в газе под действием внеш­него ионизатора R, настолько сильно ускоряются электрическим полем, что при столкно­вениях с молекулами газа ионизируют их. При этом образуются вторичные электроны и ионы. Вторичные электроны тоже ускоряются электрическим полем и в свою очередь иони­зируют новые молекулы газа. Таким образом, число носителей тока в газе и его проводи­мость сильно возрастают. В этом и состоит причина резкого увеличения тока в начале области 4. Однако ударная ионизация, производимая одними только электронами, недо­статочна для поддержания разряда после удаления внешнего ионизатора, т. е. для осущес­твления самостоятельного разряда. В самом деле, каждый электрон движется в электри­ческом поле газоразрядной трубки в направлении от катода к аноду. Поэтому он может ионизировать только те молекулы газа, которые лежат ближе к аноду по сравнению с ме­стом его собственного возникновения. Иными словами, если энергия положительных ионов недостаточна для ударной ионизации молекул газа или для выбивания электронов из металлического катода газоразрядной трубки, то вблизи последнего свободные элект­роны могут возникать только благодаря действию внешнего ионизатора. В случае внезап­ного прекращения его действия область ударной ионизации газа электронами будет со­кращаться, стягиваясь к аноду по мере движения к нему электронов, так что вскоре удар­ная ионизация газа и электрический разряд в нем прекратятся совсем.

2. Совершенно иная картина наблюдается, если напряжение Uстоль велико, что поло­жительные ионы также приобретают способность порождать вторичные электроны[2]. В этом случае образуется двусторонняя лавина электронов и положительных ионов, возникаю­щих во всех частях объема газа. Теперь внешний ионизатор уже не играет практически никакой роли в осуществлении газового разряда, так как число создаваемых им первич­ных электронов и ионов ничтожно мало по сравнению с числом вторичных электронов и

J и

2. Аналогично можно найти энергию заряженного конденсатора. Если q — заряд кон­денсатора, а Дф = ф! — ф₂ — разность потенциалов положительно и отрицательно заря­женных его обкладок 1 и 2, то для переноса малого заряда dq с обкладки 2 на обкладку 1 внешние силы должны совершить работу

ЬА' = (ф, -Фа^<7 =

где С— электрическая емкость конденсатора. Работа внешних сил при увеличении заря да конденсатора от 0 до q равна

А' *. (17.2')

{ С 2С ^{v 9}

Соответственно электрическая энергия заряженного конденсатора

_W -11 = ^g(^i ~ Фа)⁸ _ 9(Ч>1 ~ *Ра) (17.4)

2С “ 2 2

Учитывая, что конденсатор — это система из двух проводников 1 и 2, заряды которых Я\ = Ч ^и Яг = — <7, перепишем формулу (17.4) в виде

Щ = ^!/а(йФ1 +?2Фг)- (17.40

В исходной формуле (17.4) фигурирует разность потенциалов Ц — ip₂, которая не за­висит от выбора начала отсчета Щ Поэтому будем считать, что начало отсчета Ц и Ш в формуле (17.4') находится в бесконечно удаленной точке.

3. Можно показать, что электрическая энергия системы из п неподвижных заряжен­ных проводников равна

(17.5)

^ «-I

где q_{ — заряд i-ro проводника, a — его потенциал (относительно бесконечно удаленной точки) в электростатическом поле всей системы из п проводников.

В проводнике избыточные заряды распределены по его внешней поверхности, так что

= Г aidS¹,

(Si)

где a_f — поверхностная плотность свободных зарядов на малом элементе поверхности»-го проводника площадью dS, а интегрирование проводится по всей эквипотенциальной внеш­ней поверхности проводника площадью S_t. Таким образом, формулу (17.5) можно пере­писать в виде

^ = Wi^dS- ШШ

1 ^<_1 (s_t)

4. Электрическую энергию любой системы заряженных неподвижных тел — про­водников и непроводников — можно найти по формуле, являющейся обобщением фор­мул (17.5) и (17.5')

We=- fyodS + - fwdv, (17.6)

(&шряж) (Ииряж)

где о и р — поверхностная и объемная плотности свободных зарядов; ip — потенциал ре­зультирующего поля всех свободных и связанных зарядов в точках малых элементов dSH (Незаряженных поверхностей и объемов. Интегрирование проводится по всем заряжен­ным поверхностям тел системы (З^р,,,*) и по всему заряженному объему (К_Мр_МЖ) тел сис­темы, изготовленных из диэлектриков.

Основываясь на формулах (17.5) и (17.6), можно трактовать энергию МК.как потенци­альную энергию системы заряженных тел, обусловленную кулоновскими силами их вза­имодействия. Влияние на энергию системы Щсреды, в которой находятся тела системы, сказывается в том, что даже при неизменном распределении свободных зарядов значения Ф в разных диэлектриках различны. Например, в однородном, изотропном диэлектрике, заполняющем все поле, ip меньше, чем в вакууме, в е раз.

Легко видеть, что из формулы (17.6), в частности, следуют формулы (17.3) и (17.4').

В самом деле, для уединенного заряженного проводника р = 0 и потенциал ш во всех точ­ках поверхности проводника одинаков, поэтому

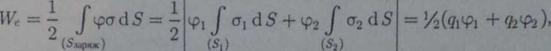
где S_x и Sj — площади обкладок конденсатора.

5. В качестве примера вычислим энергию заряженного плоского конденсатора. Элек­трическая емкость такого конденсатора С = te₀S/d, а разность потенциалов обкладок 4>i ~ Ф2 = Ed, где Е— напряженность однородного поля в конденсаторе. Подставив в (17.4) эти выражения для Си ipi — ip₂, получим

(17.7)

где V= Sd— объем поля конденсатора.

Формула (17.7) связывает энергию, затраченную на зарядку конденсатора, с основ­ной характеристикой его электрического поля — напряженностью Е. Формулы (17.4) и

(17.7) позволяют дать две различные трактовки энергии W_e. Исходя из (17.4) можно ут­верждать, что W_e — энергия системы зарядов на обкладках конденсатора, т. е. носителями электрической энергии являются сами заряды. С другой стороны, согласно (17.7), W_e — энергия электрического поля конденсатора, т. е. она распределена по всему объему поля, которое является ее носителем. Электростатическое поле неотделимо от его источни­ков — неподвижных электрических зарядов. Поэтому, оставаясь в рамках электростати­ки, нельзя отдать предпочтение какому-либо из двух вышеприведенных утверждений от­носительно локализации энергии W_e.

Изучение переменных электромагнитных полей показало, что они могут существо­вать отдельно от породивших их систем электрических зарядов и токов, а их распростра­нение в пространстве в виде электромагнитных волн связано с переносом энергии. Так было доказано, что электромагнитное поле обладает энергией. Соответственно и элект­ростатическое поле обладает энергией, которая распределена в поле с объемной плотнос­тью w_e В однородном поле плоского конденсатора его энергия W_e должна быть распреде­лена равномерно по всему объему поля V = Sd. Поэтому из (17.7) следует, что объемная плотность энергии электростатического поля плоского конденсатора

(17.8)

где D = ееоЕ — электрическое смещение.

6. Выражение (17.8) для объемной плотности энергии электростатического поля спра­ведливо также и для неоднородных полей:

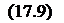= d W_e/d Щ 1 ШИ

где d W_t — энергия малого элемента d V объема поля, в пределах которого величину w_t можно считать всюду одинаковой.

Докажем это на примере энергии неоднородного поля заряженной проводящей сферы радиуса Я, окруженной однородным, изотропным диэлектриком с относительной диэлек­трической проницаемостью е. Электрическая емкость проводящей сферы равна электри­ческой емкости проводящего шара того же радиуса и может быть найдена по формуле

(16.10): С= 4еерА Если заряд сферы равен q, то ее электрическая энергия, согласно (17.3), равна

W_e=?7(8иееоЯ).

Напряженность ноля заряженной сферы, как показано в 15.4 (пример 1), равна нулю внутри сферы, а вне ее, т.е. на расстоянии от ее центра г > R, направлена радиально, при­чем Е_г — q/(4'кес₀г²). Объемная плотность энергии поля сферы

_ ИрЕ* _ серЕг _ д²

2 * 2 32ЙЩК'

Из этого выражения видно, что объемную плотность энергии поля можно считать оди­наковой в пределах тонкого шарового слоя, концентричного заряженной сфере и ограни­ченного сферическими поверхностями, радиусы которых равны г и г + dr. Объем этого слоя d V — 4itr²dr, а энергия электростатического поля в нем

(17.11)

Энергию всего поля заряженной сферы найдем путем интегрирования выражения

(17.11) по гот Л до ос:

00 Г

^J_n 8itee₀ г¹ 8тxee₀R

Это значение энергии совпадает с (17.10), что может служить подтверждением приме­нимости выражения (17.9) для расчета энергии как однородного, так и неоднородного электростатических полей:

We— Г ^££°^² dV = Г ^ dV

J >2 Щ 2 (17.12)

(мюля) (Кполя)

7. В заключение заметим, что формулы (17.5) и (17.6) пригодны только для потенци­альных электростатических полей неподвижных заряженных тел. Для переменных непо­тенциальных электрических полей понятие потенциала кр и построенные на его основе выражения (17.3) —(17.6) для энергии лишены смысла. Между тем эти поля обладают энергией, которую можно найти, пользуясь универсальной формулой (17.12).

17.2. Энергия поляризованного диэлектрика

1. Процесс поляризации диэлектрика в электрическом поле связан с затратой энер­гии. При электронной поляризации силы поля совершают работу растяжения молекул — упругих диполей, а при ориентационной поляризации силы поля совершают работу по повороту в поле электрических моментов молекул — жестких диполей. Поэтому ясно, что поляризованный диэлектрик обладает энергией, которая распределена по его объему с некоторой объемной плотностью и)_е(ДИал). Из формулы (17.9) следует, что объемная плот­ность энергии электростатического поля в вакууме (е = 1)

го_е(тк) = (17.13)

При той же напряженности 2?поля в диэлектрической среде объемная плотность энер­гии поля в е раз больше, чем в вакууме:

#². (17.14)

Поэтому объемная плотность энергии поляризованного диэлектрика

= 7г(е - l)e₀S^! = VsxeoS'-'/jPS (17.15)

где Р = хе₀Е ~ поляризованность диэлектрика, а х * ^е ~ 1 — его диэлектрическая воспри­имчивость.

2. Докажем справедливость формулы (17.15) на примере электронной поляризации диэлектрика с неполярными молекулами — упругими диполями. Связь между электри­ческим моментом р_е упругого диполя, индуцированным полем, и напряженностью Б вы­ражается формулой (15.2): р_е == ае₀Е, где а — поляризуемость молекулы. Так как р_е = q\, где 1 — плечо диполя, a q > 0 — его положительный заряд, то

l = ote₀E/9. (17.16)

При увеличении плеча диполя на dl сила F = qE, действующая со стороны поля на заряд q диполя, совершает элементарную работу 6Л = gEdl. Из (17.16) видно, что dl = = (ae₀/g)dE. Поэтому

6 А = <7 —EdE = azoEdE.

Я

Интегрируя это выражение по Е от 0 до Е_} найдем работу сил ноля при деформации одного упругого диполя:

А» ^l/2P*i£

Искомая объемная плотность энергии равна сумме работ по деформации всех По моле­кул, содержащихся в единице объема диэлектрика:

глотал) = ^ш ‘/аРЕ,

так как поляризованность диэлектрика с неполярными молекулами Р = Лор_е.

17.3. Закон сохранения энергии для электрического поля

1. Энергия W_t электрического поля какой-либо системы заряженных тел (проводни­ков и диэлектриков) изменяется, если тела системы перемещаются, а также если изменя­ются их заряды. При этом совершают работу внешние силы, приложенные к телам систе­мы, и источники электрической энергии (аккумуляторные батареи, генераторы тока и т. п.), подключенные к проводникам системы. Возможен также теплообмен между системой и внешней средой. Выделяя энергию W_e, представим полную энергию рассматриваемой системы в виде W— W_e+ U, где W_K— кинетическая энергия механического движе­ния тел системы, а U— та часть внутренней энергии системы, которая не связана с элект­рическим полем системы. Энергия {/включает в себя энергию теплового движения моле­кул, энергию их взаимодействия и т.п.

Для малого изменения состояния системы заряженных тел, согласно закону сохране­ния и превращения энергии, имеем,

d W_e + d W_K + d V- ЬА' + бЛ_и.„ + 6Q, (17.17)

где ЬА' — работа внешних сил, действующих на тела системы; ЬА_НХХ — работа источников электрической энергии в системе; bQ — количество теплоты, сообщаемое системе извне.

2. Будем считать, как это обычно бывает, что в рассматриваемых процессах температура системы поддерживается постоянной, а изменение плотности диэлектриков и теплота, вы­деляющаяся или поглощающаяся в них при изменении их поляризованности, пренебрежи­мо малы. В таком случае можно считать, что d(/«0 и bQ» —6Qa_ji, т.с. что от системы

отводится только теплота Джоуля—Ленца, которая выделяется электрическими токами, связанными с перераспределением зарядов в проводниках системы. Подставив эти значе­ния d С/и бфв уравнение (17.17), получим следующее выражение закона сохранения энергии:

d W_t + dW_K + 6<2д_д = ЬА‘ + 8^. (17.18)

3. Если перемещение тел системы производится квазистатически, т.е. очень медлен­но, то можно, во-первых, пренебречь изменением кинетической энергии системы (d W_K — = 0) и, во-вторых, считать работу внешних сил ЬА’ равной и противоположной по знаку работе б А, совершаемой силами, которые действуют на тела системы в электрическом поле

и, как отмечалось выше, называются пондеромоторными силами. В таких случаях закон сохранения энергии (17.18) можно переписать в форме

6A_UML = dW^,, + 6A-H6Q_a_j_l. (17.19)

Работа источников электрической энергии за малый промежуток времени df равна

где к— общее число источников электрической энергии в системе; «Г,— ЭДС **го источни­ка; dg, — заряд, проходящий через этот источник за время df; /, = dqjdt — сила тока в источнике. Работа > 0, если ток /, идет внутри источника от катода к аноду.

Выражение закона сохранения энергии для квазнстатического изменения состояния системы тел, в которой заряд каждого из проводников ие изменяется и не перераспреде­ляется. так что 6A.J. = 0 и bQx-д — Ос

ай; + 6Д = 0, (17.20)

Эго соотношение можно использовать для отыскания пондеромоторных сия на основе расчета изменения энергии электрического поля системы.

4. Рассмотрим в качестве примера расчет сил. действующих на пластины заряженного плоского конденсатора, расстояние между пластинами которого К VS, гае S— пластины.

Конденсатор заряжен и отключен от источника электрической энергии, так что конденсатора aS— const, где а — поверхностная плотность зарядов. При увеличении расстояния между пластинами на dx пондеромоторная сила F, приложенная к перемета* юшейся пластине, совершает работу ЬА = —/dx Изменение энергии электростатического поля в конденсаторе d W_t т где м. — объемная плотность энергии поля в при ж»»гау» шем к пластине слое толщиной dx Таким образом, из закона сохранения энергии (17.20) следует, что пондеромоторная сила равна

(1721)

Возможны два случая:

1) между пластиками конденсатора находится газообразный или м ти«*

2) между пластинами конденсатора находится твердый диэлектрик.

В первом случае все пространство между пластинами конденсатора независимо от рас* стояния между ними заполнено одним и тем же диэлектриком с относительной диалект - рической проницаемостью с. Следовательно,

■Ь* сс»£*/2 =* ^/(SkJ,

0*S/(tее*) «/**/€, (1722)

wf^-cwitii^ByiiWMMBJMtnt^iwroBtHiiuriKiiayi^iwMBtBBiHBHa, юшшю в отсутствие диэлектрика, т.в. в вакууме.

Во втором случае в слое толщиной с1д^ образовавшемся в результате отодвигания пла­стины конденсатора, находится воздух, относительная диэлектрическая проницаемость которого равна единице. Поэтому

w_e — е₀(Е^,т)*/2 — сг²/(2е₀),

F— a²S/(2е₀) = F"*. (17.22')

5. Независимость сил взаимного притяжения пластин заряженного плоского конден­сатора с твердым диэлектриком от диэлектрической проницаемости е последнего понят­на: напряженность поля пластин зависит от е (уменьшается в е раз по сравнению с напря­женностью поля в вакууме) только внутри диэлектрика, а пластины конденсатора находятся вне диэлектрика, где напряженность поля равна Е^т,н. Однако эти рассуждения в равной мере применимы и к конденсатору с жидким или газообразным диэлектриком. Поэтому специального обсуждения требует соотношение (17.22), получающееся в этом случае из закона сохранения энергии. Нужно понять механизм уменьшения силы взаим­ного притяжения пластин конденсатора ири заполнении его жидким или газообразным диэлектриком.

У краев плоского конденсатора его электростатическое поле неоднородно: напряжен­ность быстро уменьшается по мере удаления от края пластин конденсатора вовне. На мо­лекулы-диполи жидкого или газообразного диэлектрика, находящиеся в таком сильно неоднородном поле, действуют силы, которые втягивают эти диполи в область более силь­ного поля, т.е. внутрь конденсатора. Поэтому, согласно закону Паскаля, давление р ди­электрика внутри заряженного конденсатора больше, чем атмосферное давление ро вне конденсатора. Следовательно, результирующая сила /•’притяжения пластин меньше силы F*"' их кулоновского притяжения на величину гидростатической силы (р — Po)S:

F^ш - (р- Po)S.

Закон сохранения энергии позволил найти силу F, а следовательно, и (р - ро), не вни­кая во внутренний механизм влияния диэлектрика на F.

Вопросы

1. Как найти электрическую энергию системы заряженных тел (проводников и непроводни­ков)? Где локализована эта энергия?

2. Выведите выражение для объемной плотности энергии электрического поля.

3.Дайте качественное объяснение уменьшения силы взаимного притяжения пластин заряжен­ного плоского конденсатора при погружении его в жидкий диэлектрик.

[1] Формула Стокса (20.5) справедлива для шара, движущегося в газе, только при условии, что радиус шара во много раз больше средней длины свободного пробега молекул газа. В опытах М кл- ликона масляные капли были столь малы, что это условие не выполнялось. Поэтому при обработке своих опытных данных Милликен ввел необходимые поправки в формулы (20.5)—(20.9).

[2] Опыты показывают, что в большинстве случаев для выбивания электрона из катода положи­тельный ион должен совершать меньшую работу, чем для ударной ионизации молекул газа. Поэто­му основной причиной появления вторичных электронов под действием положительных ионов является процесс выбивания электронов из катода газоразрядной трубки.

[3] nu 2т-

Дата добавления: 2014-01-04