Закон сохранения энергии для электромагнитного поля

Рассмотрим замкнутый объем, в котором электромагнитное поле возбуждается переменными токами с объемной плотностью .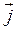

По закону Джоуля-Ленца в дифференциальной форме: .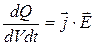

Найдем количество теплоты, выделяющееся в единицу времени в этом объеме: .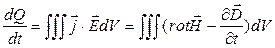

Используем, что .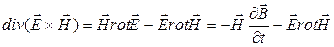

Тогда: .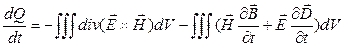

По теореме Гаусса: .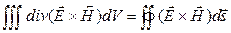

Слагаемые во втором интеграле можно представить в виде:

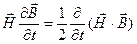так как .

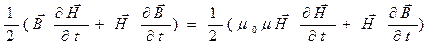Аналогично можно представить: .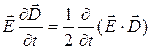

Тогда: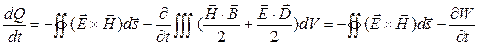

Подинтегральное векторное произведение напряженностей электрического и магнитного полей также представляет собой вектор 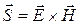, направленный по скорости распространения электромагнитной волны и равный по величине в любой момент времени: 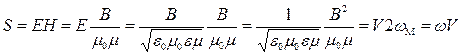. При выводе этого соотношения использовано понятие объемной плотности энергии магнитного поля, которая, как показано Максвеллом, равна половине объемной плотности энергии электромагнитного поля.

Соответственно, для характеристики переноса энергии электромагнитной волной, вводится вектор Умова-Пойтинга 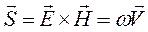, - плотность потока электромагнитной энергии через поверхность, ограничивающую рассматриваемый объем. Таким образом можно рассчитать поток энергии, проходящей через поверхность, ограничивающую данный объем: .

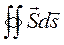Выражение: 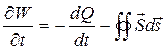представляет собой закон сохранения энергии электромагнитного поля, так как показывает, что изменение энергии электромагнитного поля в объеме определяется тепловой мощностью и потоком энергии через поверхность, ограничивающую объеме. Если тепловых потерь нет, то 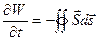или 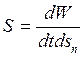, т.е. вектор Умова-Пойтинга определяется энергией, проходящей в единицу времени через единичную поверхность, перпендикулярную направлению распространения волны. Полную энергию поля в рассматриваемом объеме можно, следовательно, рассчитать по формуле: .

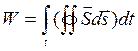Силы в магнитном поле. Силы, действующие на ток. Сила Лоренца. Силы и момент сил действующие на магнитный момент.

На точечный заряд в электрическом поле действует сила:

.

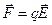На непрерывно распределенный заряд:

,

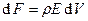объемная плотность сил:

.

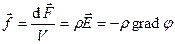Объемные силы, действующие на диэлектрик – это сумма сил, действующих на диполи внутри диэлектрика.

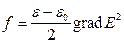- особенно для жидкостей и газов.

Под действием элементарных сил на малые объемы эти элементы сдвигаются в направление роста 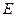. На поверхности раздела сила всегда направлена в сторону диэлектрика с меньшим .

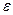Силы в магнитном поле: 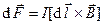, объемная плотность сил 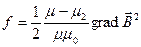. У диамагнетиков 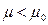, поэтому сила направлена в сторону уменьшения магнитного поля.

Работа, которая совершается током, не является результатом превращения кинетической энергии электронов в другие виды энергии. Носитель энергии – не электроны, а поля. В частном случае джоулева тепла кинетическая энергия электрона не является промежуточной формой энергии.

Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды. Сила, действующая на электрический заряд 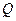, движущийся в магнитном поле со скоростью 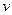, называется силой Лоренца и выражается формулой

,

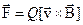где 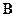- индукция магнитного поля, в котором заряд движется.

Модуль силы Лоренца равен:

,

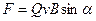где 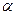- угол между 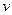и .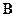

Направление силы Лоренца определяется с помощью правила левой руки.

Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает.

Если на движущийся электрический заряд помимо магнитного поля с индукцией 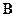действует и электрическое поле с напряженностью 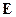, то результирующая сила 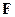, приложенная к заряду, равна векторной сумме сил:

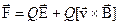
Это выражение называется формулой Лоренца. Рассмотрим действие магнитного поля на замкнутый контур с током. Для характеристики плоского контура с током вводят вектор магнитного момента 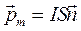, где S – площадь, ограниченная контуром, а направление нормали связано правилом правого винта с направлением тока в контуре (рис.84).

Рассмотрим плоский контур в однородном магнитном поле. Сила, действующая со стороны магнитного поля на весь контур на основании закона Ампера равна: .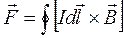

Так как сила тока и магнитная индукция при указанных условиях постоянны, то их можно вынести из-под знака суммы, а сумма элементарных векторов 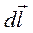, в виде цепочки которых можно представить контур, равна нулю (рис.85).

Если результирующая сила равна нулю, то центр масс контура будет оставаться неподвижным, т.е. контур не будет двигаться поступательно, но возможно вращательное движение. Найдем вращающий момент сил, действующих на контур.

Рассмотрим простейший случай – линии вектора магнитной индукции лежат в плоскости контура. Разобьем контур на бесконечно узкие полоски шириной 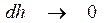, параллельные линиям индукции.

Каждая полоска ограничена элементами тока, на которые со стороны магнитного поля действуют силы 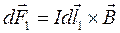и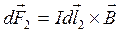

перпендикулярные плоскости чертежа и противоположные по направлению.

, .

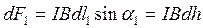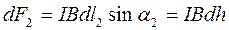Величина момента этой пары сил (равные по величине и противоположные по направлению):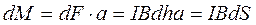

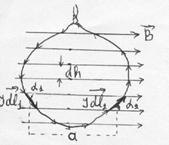
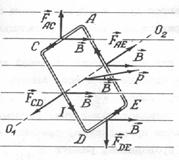
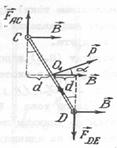
РИС.84 РИС.85 РИС.86

Моменты сил действующих на все пары элементов тока контура направлены в одну строну и величина момента, действующего на весь контур .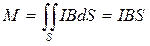

Следовательно, в этом случае при 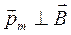, величина вращающего момента равна 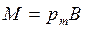.В общем случае и 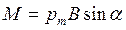.Вращающий момент равен нулю пр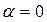и и 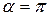. В первом случае 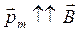и положение контура устойчивое.

Дата добавления: 2014-01-04