Апериодический разряд конденсатора на катушку и резистор

Рассмотрим процесс разряда конденсатора на резистор R и катушку L. Если параметры контура из резистора, катушки и конденсатора удовлетворяют условию 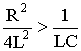или 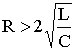, то корни характеристического уравнения контура вещественные, различные, т.е. р₁ ≠ р₂, и отрицательные. В этом случае напряжение на конденсаторе описывается уравнением

u_C = u_Cсв = A₁ · e^p₁^t + A₂ · e^p₂^t,

где А₁ и А₂ – постоянные интегрирования, определяемые из начальных, условий.

Свободный ток равен

.

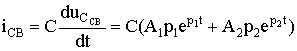Установившиеся составляющие напряжения на конденсаторе и тока равны нулю. Поэтому их переходные значения равны свободным составляющим:

u_C = u_Cсв; i = i_св.

Определим из начальных условий постоянные интегрирования А₁ и А₂. При t = 0, u_C(0) = U₀ и i(0) = 0. Подставив их в выражения для переходных напряжений и токов при t = 0 имеем

U₀ = A₁ + A₂; 0 = A₁ p₁ + A₂ p₂.

Отсюда

A₁ = U₀ p₂ / (p₂ - p₁); A₂ = -U₀ p₁ / (p₂ - p₁);

С учетом начальных условий запишем

; .

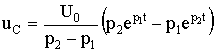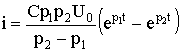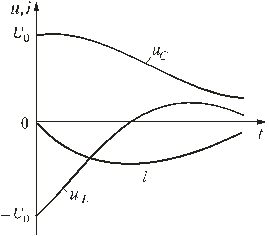
Рис. 1.14

Произведение корней по теореме Виета: p₁ p₂ = 1 / (LC), следовательно, ток

.

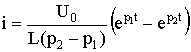Напряжение на катушке

.

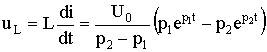Графики зависимости тока и напряжения от времени, показанные на рис. 1.14 позволяют говорить об апериодическом разряде конденсатора. Апериодическим называется такой разряд, при котором конденсатор все время разряжается, т.е. функция u_C(t) - убывающая, а ток i не меняет своего направления, в нашем случае он отрицателен. Сделаем некоторые выводы.

1. Апериодический разряд конденсатора в цепи R, L, С возникает при вещественных, отрицательных и неравных корнях характеристического уравнения.

2. При апериодическом разряде напряжение на конденсаторе уменьшается от начального значения до нуля, а ток сначала возрастает по модулю, затем уменьшается, проходя через максимальное значение.

3. Напряжение на катушке уменьшается от начального значения, проходит через нулевое значение, изменяя знак и, достигнув наибольшего значения, уменьшается до нуля.

Дата добавления: 2014-01-04