Группа единиц

Число классов числового поля

6.10.1. Лемма. Пусть K – алгебраическое числовое поле степени n. Для всякого целого m > 0 число идеалов a Ì O _K, для которых N (a) £ m, конечно.

6.10.2. Лемма. Пусть K – алгебраическое числовое поле степени n. Существует константа C, зависящая лишь от поля K, такая, что всякий целый идеал a ¹ (0) кольца O _K содержит z ¹ 0, такое, что ½ N_K (z)½ £ C × N (a).

6.10.3. Теорема. Число классов числового поля K конечно.

◄ Мы докажем, что во всяком классе эквивалентности ненулевых дробных идеалов содержится целый идеал нормы £ C, где C – константа, зависящая лишь от поля K. По лемме 6.10.1 число классов h тогда конечно. Пусть K – класс эквивалентных идеалов из группы C _K. Выберем идеал a в обратном классе K^-1. Из определения дробного идеала следует, что без ограничения общности идеал a можно предполагать целым. Имеем a^-1 Î K. По лемме 6.10.2 существует z Î a, такое, что ½ N_K (z)½ £ C × N (a) для константы C = C (K). Пусть теперь b = (z)a^-1. Так как b ~ a^-1, то b Î K. Тогда N (a) N (b) = N (ab) = N (z O _K) =½ N_K (z)½£ C × N (a). Сокращая на N (a), получаем N (b) £ C. Кроме того, так как z O _K Ì a, то b = z a^-1 Ì aa^-1 = O _K, т.е. b – целый идеал кольца O _K. Это завершает доказательство теоремы. ►

6.10.4. Г. Минковский доказал ещё более сильный результат. Пусть K – алгебраическое числовое поле степени n с дискриминантом d_K, 2 s – число комплексно сопряжённых с K полей. Тогда всякий класс ненулевых дробных идеалов содержит целый идеал a с нормой

N (a) £ .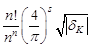

Число B_K, стоящее в правой части неравенства называется границей Минковского, число
C_K = 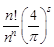- константой Минковского.

Примеры. 1) Пусть K = Q(i), дискриминант d_K = -4 и 1, i - целый базис поля K, т.е. O _K = = Z[ i ]. В силу примера 2.6.8 r = 0, s = 1. Граница Минковского равна B_K» 1,272. Тогда для любого представителя a класса дробных идеалов выполняется неравенство N (a) £ 1,272, т.е.
N (a) = 1, следовательно, a = O _K. Таким образом, h_K = 1.

2) Пусть K = Q(). Имеем r = 2, s = 0, дискриминант d_K = 8, граница Минковского B_K = =. В таком случае для любого целого представителя a класса дробных идеалов выполняется неравенство N (a) £, т.е. N (a) = 1 и, значит, a = O _K. Таким образом, h_K = 1.

3) Пусть K =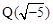. Имеем r = 0, s = 1, d_K = -20, граница Минковского равна B_K» 2,847. В таком случае для любого представителя a класса дробных идеалов выполняется N (a) £ 2, т.е. N (a) = 1 и, значит, a = O _K, или N (a) = 2. Согласно 6.7.4 2) a – простой идеал. В силу 6.7.5
N (a) = 2 Î a, следовательно, a½2O _K. Из разложения идеала 2O _K в произведение простых получаем a = (2, 1 +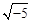). Если a ~ O _K, т.е. a = t O _K для некоторого t = a + 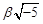Î O _K, где a, b Î Z, то N (a) = N (t O _K) =½ N_K (t)½, т.е. 2 = a ² + 5 b ². Однако это равенство невозможно в Z. Следовательно, a ≁ O _K. Таким образом, h_K = 2.

6.11.1. Пусть K – алгебраическое числовое поле степени n, K ⁽¹⁾ = K, K ⁽²⁾,..., K ^{( n )} – все сопряжённые с K поля. Если s ₁, s ₂,..., s_n – различные вложения поля K в поле C комплексных чисел, то K ^{( i )} = s_i (K) для 1 £ i £ n. Если z Î K, то для 1 £ i £ n обозначаем z ^{( i )} = s_i (z) - сопряжённые с z числа.

6.11.2. Лемма. Пусть C > 0. Число алгебраических целых z Î O _K, таких, что ½ z ^{( i )}½ £ C для 1 £ i £ n, конечно.

6.11.3. Определение. Комплексное число z называется корнем из единицы, если
z^m = 1 для некоторого m Î Z, m ¹ 0.

6.11.4. Пусть K – алгебраическое числовое поле.

1) Если z - корень из единицы в K, то z^m = 1 для некоторого m Î Z, m ¹ 0, так что s_i (z) ^m = (z ^{( i )}) ^m = 1, откуда ½ z ^{( i )}½= 1 для 1 £ i £ n.

2) Всякий корень из единицы в K есть единица и, следовательно, принадлежит O _K, но обратное не всегда верно.

3) Корни из единицы в K, очевидно, образуют группу m (K) относительно умножения.

6.11.5. Предложение. Число корней из единицы в алгебраическом числовом поле K конечно.

6.11.6. Предложение. Пусть K – алгебраическое числовое поле. Группа m (K) корней из единицы в K является конечной и циклической.

6.11.7. Теорема (Дирихле). Пусть r – число вещественных вложений поля K в C, 2 s – число комплексных и t = r + s – 1. Тогда существуют единицы e ₁, e ₂,..., e_t и корень из единицы z в O _K, такие, что всякая единица e Î 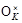может быть записана в виде

e = ,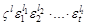

где l, l ₁, l ₂,..., l_t Î Z. При этом числа l_i, i ³ 1, определяются единственным образом, а число l – единственным образом по модулю w, где w есть порядок ½ m (K)½ группы m (K) корней из единицы в K. Иными словами, 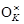@ m (K) ´ Z ^t.

Примеры. 1) Пусть K = Q(i). Очевидно

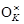= m (K) = {±1, ± i } = { i, i ², i ³, i ⁴ = 1} @ Z / 4Z.

2) Пусть K = Q(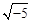). O _K = Z[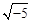]. Если e = a + b 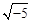принадлежит 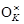, то N_K (e) =

= a ² + 5 b ² = 1. Это возможно лишь, когда a = ±1, b = 0, т.е. e = ±1. Таким образом, =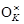
= m (K) = {±1} = {-1, (-1)² = 1} @ Z/2Z.

Дата добавления: 2014-01-04