Энергетические уровни атома. Квантовые числа

Состояние атома можно охарактеризовать через состояние его электронов. Электрон – движущаяся заряженная частица, поэтому для его характеристики необходимы четыре величины: два механических момента импульса и два магнитных момента.

Орбитальный момент импульса и орбитальный магнитный момент обусловлены вращением электрона вокруг ядра.

Собственный момент импульса (спин) и спиновой магнитный момент обусловлены вращением электрона вокруг собственной оси.

С моментами связаны квантовые числа. Их также четыре:

1. Главное квантовое число: n = 1, 2, 3,… (числа натурального ряда). Характеризует местонахождение электрона в атоме, его удалённость от ядра. В модели Резерфорда-Бора определяет радиусы круговых орбит вращения электронов вокруг ядра. Радиусы должны удовлетворять условию квантования (орбитальный момент импульса электрона кратен постоянной Планка):

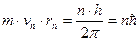, где

m – масса электрона,

v_n – скорость электрона на данной орбите,

r_n – радиус орбиты.

Чем больше n, тем дальше от ядра орбита, больше скорость и энергия электрона на этой орбите и энергия атома в целом.

Боровская модель атома – удобное приближение, однако на самом деле невозможно точно указать одновременно энергию электрона и его местонахождение.

Электронная орбита – лишь наиболее вероятная область локализации электрона в атоме.

Совокупность всех электронов с одинаковым квантовым числом n – электронный слой. Изменение n – переход из одного электронного слоя в другой.

2. Орбитальное квантовое число: l = 0, 1, 2, …, n -1 (целые числа от нуля до «n -1»). В рамках Боровской модели характеризует форму электронной орбиты.

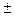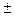3. Магнитное квантовое число: m_l = 0, 1, 2, … 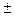n. Характеризует пространственное расположение орбиты, определяет проекцию орбитального магнитного момента электрона на вектор напряжённости внешнего магнитного поля.

4. Спиновое квантовое число: m_s = 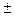½. Определяет проекцию спинового магнитного момента электрона на вектор напряжённости внешнего магнитного поля.

При изменении любого из четырёх квантовых чисел меняется энергетическое состояние как электрона, так и атома в целом.

Система энергетических уровней и подуровней молекулы.

Внутренняя энергия молекулы включает следующие составляющие:

1. Энергия движения электронов в атомах (E_эл)

2. Энергия колебательного движения атомов в молекуле (Е_кол)

3. Энергия вращательного движения самой молекулы как целого (Е_вр)

Е_м = Е_эл + Е_кол + Е_вр

Энергия колебательного и вращательного движения тоже квантуется, следовательно, у молекулы появляются дополнительные энергетические подуровни:

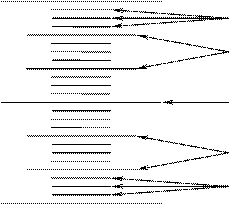вр.

кол.

эл.

кол.

вр.

Кванты уменьшаются в ряду: Е_эл → Е_кол → Е_вр. Поэтому радиоволны СВЧ-диапазона и дальний ИК-свет возбуждают лишь переходы между вращательными уровнями. Близкий ИК-свет – переходы между колебательными и вращательными уровнями. В области видимого и УФ-света – все три вида переходов (между электронными, колебательными и вращательными уровнями).

Дата добавления: 2014-01-04