Лекция 4. Если событие А реализуется при осуществлении одного из событий

§ Формула полной вероятности

Если событие А реализуется при осуществлении одного из событий

Н₁, Н₂, …Н_n (или гипотез), которые образуют полную группу событий

(т.е.: 1. 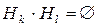и 2. 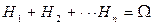), то вероятность наступления события А равна сумме произведений вероятностей гипотез на соответствующую условную вероятность события А: 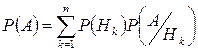- ФПВ

Доказательство:

Так как Н₁, Н₂, …Н_n образуют полную группу событий, то событие А можно представить как пересечение n несовместных событий:

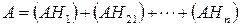
По III аксиоме Теории Вероятностей (вероятность суммы независимых событий равна сумме их вероятностей):

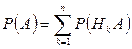и по Теореме произведения вероятностей зависимых событий (Н_k и А – в свою очередь зависимые события):

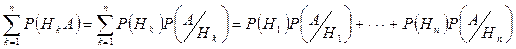ч.т.д.

К формуле полной вероятности (ФПВ) применимо контрольное равенство: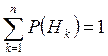

Пример 1: По каналам связи передается одна из последовательностей:

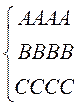с соответствующими вероятностями p₁, p₂ и p₃;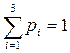

Каждая принимаемая буква принимается с вероятностями: α – за правильную, 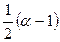и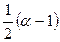– за неправильные. Предполагается, что буквы искажаются независимо друг от друга.

Задание: 1. Какова вероятность того, что принята комбинация АВСА при условии передачи комбинации АААА?

2. Какова вероятность того, что принята комбинация АААА при условии передачи комбинации АВСА?

Решение:

1. Пусть событие 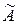символизирует то, что принята комбинация АВСА, тогда гипотезы:

Н₁ – передана комбинация АААА

Н₂ – передана комбинация ВВВВ

Н₃ – передана комбинация СССС, и: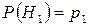

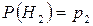
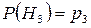
Найдем условную вероятность события 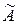при условии Н₁:

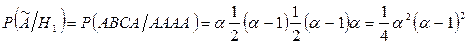
Найдем условную вероятность события 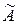при условии Н₂:

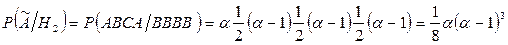
Найдем условную вероятность события 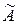при условии Н₃:

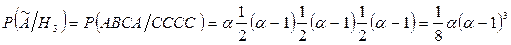
Теперь подсчитаем вероятность события 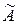по ФПВ:

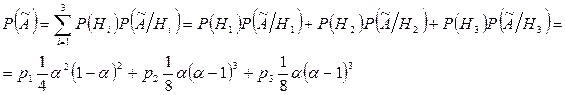
При решении второго задания нам придется применить формулу Байеса:

При выводе формулы Байеса сохраняются все предположения, принятые при выводе ФПВ и ставятся дополнительные условия: при проведении опыта событие А уже произошло. Это позволяет переоценить первоначальные вероятности гипотез:

P(Н₁), P(Н₂) и P(Н_n) – априорные, т.е. доопытные вероятности.

Проводят испытание в отношении события А, которое может произойти лишь при осуществлении одной из гипотез. После того, как событие А произошло, можно уточнить (произвести переоценку) априорных вероятностей, т.е. вычислить вероятности 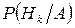– такие вероятности будут называться апостериорными.

Для условных вероятностей используется формула:

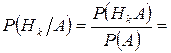и заменяем в формуле P(А) на ФПВ, а в числителе получаем произведение зависимых событий 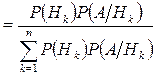- Формула Байеса

Пример 1: продолжение

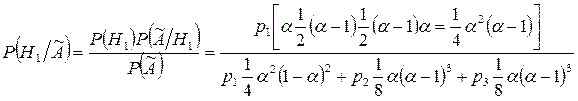
Пример 2:

В тире находятся 7 ружей: 2 – с оптическими прицелами, 5 – без. Вероятность попадания в цель из оптического орудия равна 0,9. Из неоптического – 0,4.

Задание: какова вероятность того, что стреляли из оптического орудия, при условии, что цель поражена?

Решение:

Пусть событие А символизирует поражение цели, тогда гипотезы – Н₁ и Н₂ – будут означать соответственно выстрел из оптического ружья и ружья без оптического прицела.

Таким образом, вероятности выстрела (конкретно в этом тире) из оптического ружья P(Н₁) = 2/7 и выстрела из ружья без оптического прицела P(Н₂) = 5/7 – из условия.

P(А/Н₁) = 0,9 и P(А/Н₂) = 0,4

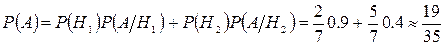
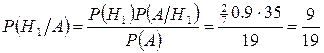
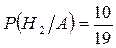
Итак, оказывается вероятность попадания в цель из ружья без оптического прицела оказалась больше вероятности поражения цели из оптического.

§ Сложные испытания. Испытания по схеме Бернулли

Пусть проведено n испытаний по событию А. Совокупность таких экспериментов будем обозначать так: 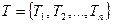и называть “сложным испытанием” или “композицией испытаний”.

В результате каждого простого испытания T_i, 1 ≤ i ≤ n, может произойти 2 случая: событие А_i произошло или не произошло, а т.е. произошло событие Ā_i

Пусть проводится сложное испытание из n независимых в совокупности испытаний, в каждом из которых лишь 2 исхода: А_i – успех, Ā_i – неудача, при условии, что в каждом испытании вероятность успеха – это постоянная величина 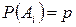и неудачи .

Такая схема независимых испытаний с двумя исходами с постоянными вероятностями называется схемой Бернулли.

Теорема Бернулли: Если по отношению к событию А проведено n испытаний по схеме Бернулли, то вероятность наступления события А ровно k раз вычисляется по следующей формуле:

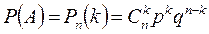, где 0 ≤ k ≤ n, 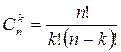- Биномиальный коэффициент, а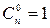

Вероятность P_n(k) называется биноминальной, т.к. это член разложения бинома Ньютона: 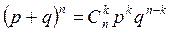, 0 ≤ k ≤ n

Доказательство: Для n=3

Возможны следующие реализации появления события А в трех испытаниях: А₁, А₂ и А₃ и тогда эти 3 независимые испытания можно представить в виде:

А₁ Ā₂ Ā_3, Ā₁ А₂ Ā₃ и Ā₁ Ā₂ А₃ ; количество таких реализаций, соответственно 3:

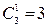
Тогда вероятность наступления события А в трех испытаниях 1 раз будет высчитываться так: 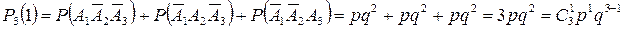Ч.Т.Д.

Пример 3: Проведено 3 выстрела по мишени. Вероятность попадания в цель равна 0,4.За каждое попадание в цель стрелку присуждается 5 очков.

Задание: Какова вероятность того, что стрелок получит 10 очков после трех выстрелов?

Решение: n = 3, k = 2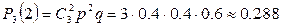

Дата добавления: 2014-01-04