Лекция 11. Обозначается и вычисляется значения вероятностей с помощью таблицы:

Правило 3 сигм

Обозначается 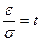и вычисляется значения вероятностей с помощью таблицы:

При t = 1: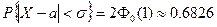

t = 2:

t = 3: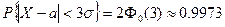

Это означает, что в 1 случае 68,28% значений НСВ попадут в данный промежуток; во 2 случае 95,45%, а в 3 случае почти все значения НСВ в этот интервал.

§ Закон равномерной плотности

R([a;b])

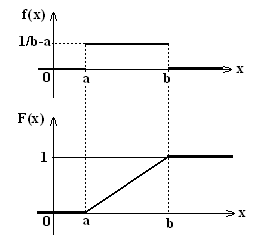
НСВ Х распределена по закону равномерной плотности на промежутке [а; b], если её плотность вероятностей f(x) – постоянная на отрезке, а вне отрезка равна 0: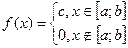

Замечание: Вместо [а;b] можно написать (а;b) или [а;b), (а;b], т.к. Х – величина случайная. Т.к.

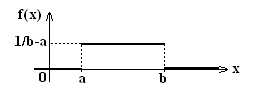
Вычислим интегральную функцию: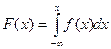

1. x < a: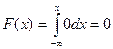

2. a ≤ x ≤ b: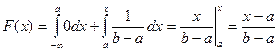

3. x > b:

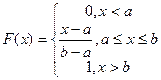
Формулы для М(X) и D(X)

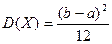
Доказательство: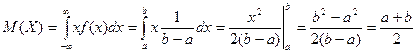

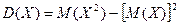
Замечание: Вероятность попадания равномерно распределённой СВ Х на интервал (x', x") из промежутка [a; b],

вычисляются по формуле:

Таким образом, вероятность попадания СВ Х в промежуток (x', x") пропорциональная длине всего промежутка.

К таким СВ, имеющим равномерное распределение относится:

- ожидание пассажирами транспорта, курсирующего с определённым интервалом t;

- ошибка округления числа до целого - на отрезке [-1/2; 1/2] и др.

Пример 1: На перекрёстке стоит светофор, по которому: 60 сек - зелёный свет, 30сек - красный, 6 сек - жёлтый. Некто подъезжает к перекрёстку в случайный момент времени, не связанный с работой светофора. Найти вероятность того, что машина не остановится (Шофер соблюдает ПДД).

Х - момент проезда машины через перекрёсток.

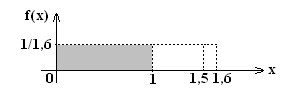
По условию СВ Х - распределена равномерно в интервале равном периоду смены цветов в светофоре, длина которого равна сумме всех значений: 1+0,5+0,1=1,6

Для того чтобы машина не остановилась, нужно, чтобы момент ее проезда приходился на промежуток (0;1). Т.е. нужно найти вероятность того, что:

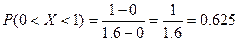. с вероятностью 0,625 машина проедет без остановки:

Пример 2: Поезд метрополитена идёт с интервалом в 3 минуты. Пассажир выходит на платформу в произвольный момент времени. Найти среднее значение ожидания поезда (М(X)), Д(X) и σ(X).

Пусть Т – НСВ – время ожидания – распределена равномерно на промежутке [0; 180сек].

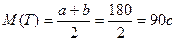
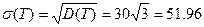
Найти вероятность того, что промежуток времени Т составит от 30 до 60 секунд.

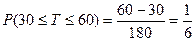
§ Показательное (экспоненциальное) распределение

Ехр(λ) λ > 0

НСВ имеет экспоненциальное распределение по параметру λ, если f(x) определяется следующей формулой:

НСВ Х ≈ Ехр (λ)

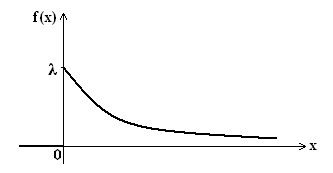
Найдем интегральную функцию:

1. x < 0: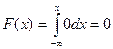

2. x > 0: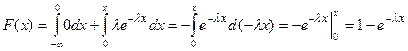

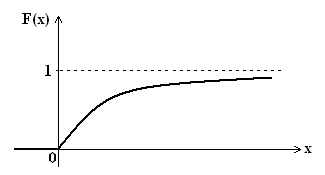
Посчитаем М(Х) и D(Х):

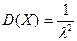
Доказательство:

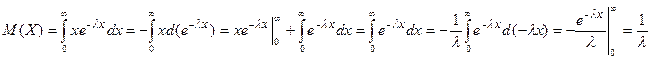
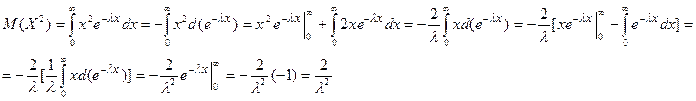
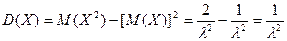
Найдём медиану:

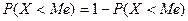
Здесь медиана – это квантиль порядка 1

Пусть Х = Мe, тогда: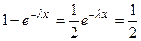

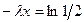
Показательное распределение применяется для описания распространения реальных событий – таких СВ, как:

- длительность работы прибора до 1-го отказа;

- длительность времени обслуживания в системе массового обслуживания и т.д.

Пример 1: Средняя длительность СВ Х – телефонного разговора – 5 мин. Найти вероятность того, что производимый разговор будет продолжаться от 5 до 10 минут.

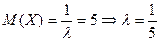
По другому:

Пример 2: Длительность времени безотказной работы каждого элемента из трех, входящих в устройство, имеет показательное распределение. Среднее время безотказной работы элемента – 500 часов. Устройство работает при условии безотказной работы всех трех элементов. Определить вероятность того, что время безотказной работы устройства составит не менее 800 часов, если время безотказной работы элемента не зависит от двух других.

Пусть А_к – следующее событие: каждый элемент проработает 800 часов.

Тогда, искомая вероятность, т.е. вероятность того, что в течение не менее 800 часов устройство будет работать, считается следующим образом:

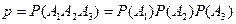
Найдём Р(А_к): Пусть случайная величина Т - время безотказной работы каждого элемента. По условию:

Найдём интегральную функцию: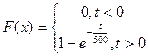

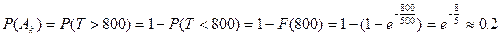
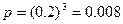
Дата добавления: 2014-01-04