
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамика текучего тела
Динамика изучает законы движения жидкости и газа в зависимости от приложенных сил. Параметры, характеризующие движение (скорость, ускорение, давление) изменяются в потоке жидкости в пространстве и во времени. В динамике часто выделяют раздел кинематики жидкости и газа, в котором изучают виды и кинематические характеристики движений жидкости, но не рассматривают силы, под действием которых происходит движение.
Тема 15 Основные понятия движения жидкости и газа
Мгновенная местная скорость u – скорость частицы жидкости в данный момент времени в каждой точке в пределах движущегося потока.
Векторное поле скоростей – совокупность мгновенных местных скоростей.
Векторными линиями поля скоростей являются линии тока. Линия тока – кривая, в каждой точке которой в данный момент времени вектор местной скорости направлен по касательной. Важной особенностью совокупности линий тока в фиксированный момент времени является то, что они не пересекаются друг с другом.
Траектория движения частицы жидкости – геометрическое место последовательных положений элементарной частицы жидкости при её движении в пространстве. Другими словами – это след движения отдельной частицы жидкости в пространстве. При установившемся движении линии тока и траектории движения жидкой частицы совпадают.
Совокупность линий тока, проведенных через все точки бесконечно малого замкнутого контура, образует поверхность, называемую трубкой тока. Поверхность трубки тока является непроницаемой, то есть жидкость не может ни вытекать из неё, ни поступать в неё.
Элементарная струйка жидкости – масса жидкости внутри трубки тока. При неустановившемся движении форма трубки тока непостоянна.
При установившемся движении трубка тока и элементарная струйка остаются неизменными.
Свойства элементарной струйки
1. Длина её неограниченна, а сечение очень мало.
2. Вследствие малости поперечного сечения элементарной струйки скорости во всех точках её поперечного сечения являются одинаковыми.
3. Поверхность является непроницаемой для частиц жидкости, движущихся в соседних струйках.
Совокупность элементарных струек, движущихся с разными скоростями и скользящими одна по другой, называется потоком жидкости.
По характеру изменения поля скоростей во времени движение жидкости делится на установившееся и неустановившееся.
Неустановившееся (нестационарное) движение такое, при котором в точках области, где движется жидкость, местные скорости изменяются с течением времени. При неустановившемся движении все элементы движения (скорость u, ускорение j, давление р, плотность r, глубина h) являются функцией и координат (x, y, z) и времени t:
u = f (x, y, z, t);
j = f (x, y, z, t); (15.1)
p = f (x, y, z, t).
Установившееся (стационарное) движение такое, при котором поле скоростей не меняется с течением времени. В любой точке потока жидкости скорость, давление и ускорение остаются постоянными, то есть не изменяются во времени ни по величине, ни по направлению:
u = f (x, y, z);
j = f (x, y, z); (15.2)
p = f (x, y, z).
Установившееся движение может быть равномерным и неравномерным.
Равномерным называется такое установившееся движение, при котором живые сечения потока и средняя скорость v в них одинаковы по его длине, а скорости в соответствующих точках всех живых сечений также одинаковы. При равномерном движении линии тока представляют собой систему прямых параллельных линий, поэтому такое движение называют также параллельно-струйным или продольно однородным.
Неравномерным называется такое установившееся движение жидкости, при котором живые сечения и средние скорости потока изменяются по его длине.
При неравномерном движении, когда линии тока непараллельны и (или) криволинейны различают:
· резкоизменяющееся движение;
· плавноизменяющееся движение, при котором можно пренебречь кривизной линий тока и их непараллельностью (угол расхождения между отдельными линиями тока очень мал). При этом с достаточной для практических целей точностью можно построить плоское живое сечение. Давление распределяется по живому сечению по гидростатическому закону, то есть по закону прямой линии.
Движение жидкости можно рассматривать в одномерном приближении, когда продольные размеры потока во много раз превосходят его поперечные размеры. Это имеет место главным образом в трубах, реках и каналах. При этом на неподвижных границах скорость жидкости равна нулю.
В гидрогазодинамике потоки разделяют на напорные, безнапорные и струйные. Если поток со всех сторон ограничен твёрдыми стенками, то он называется напорным. Если только часть потока ограничена твёрдыми стенками, а на остальной части жидкость граничит с газом, в частности с атмосферой (поток имеет свободную поверхность), то такое движение называется безнапорным. Если поток не ограничен твёрдой поверхностью, то он называется струйным (или струёй). Струя жидкости может быть ограничена той же самой жидкостью (затопленная струя) или газом (свободная струя).
Объёмным расходом потока Q называется объём жидкости V, проходящий в единицу времени t через живое сечение потока, м3/с:
Q = 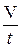 . (15.3)
. (15.3)
Массовым расходом потока Qm называется масса жидкости m, проходящий в единицу времени t через живое сечение потока, кг/с:
Qm = 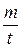 . (15.4)
. (15.4)
Живым сечением потока w называют поперечное сечение потока, перпендикулярное его направлению.
Смоченный периметр c (хи) – часть периметра живого сечения, на которой жидкость соприкасается с твёрдыми стенками.
Гидравлическим радиусом R называют отношение площади живого сечения потока w к смоченному периметру c:
R = 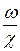 . (15.5)
. (15.5)
В случае напорного течения в круглой трубе R = 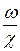 =
=  =
= 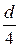 , то есть гидравлический радиус вдвое меньше геометрического.
, то есть гидравлический радиус вдвое меньше геометрического.
Диаметр эквивалентный dэкв – отношение четырёх площадей живого сечения потока w к смоченному периметру c:
dэкв =  = 4 × R. (15.6)
= 4 × R. (15.6)
Средней скоростью потока v в данном сечении называют отношение объёмного расхода потока Q к площади его живого сечения w, м/с:
v = 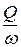 . (15.7)
. (15.7)
Если речь идёт о массовом расходе, то средняя скорость определяется из выражения:
v =  . (15.8)
. (15.8)
Тема 16 Уравнения полей скоростей и ускорений
(уравнения кинематики Эйлера)
Движение жидкости характеризуется, в основном, параметрами движения – скоростью и ускорением.
При неустановившемся движении поле скоростей изменяется во времени, то есть для одной и той же точки пространства скорость движения жидкости различна в различные моменты времени.
Обозначим через ux, uy, uz проекции скоростей на оси координат. Тогда неустановившеесядвижение потока жидкости описывается системой уравнений:
ux = f1 (x, y, z, t);
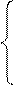
uy = f2 (x, y, z, t); (16.1)
uz = f3 (x, y, z, t).
Величина полной скорости равняется:
u = 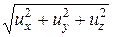 . (16.2)
. (16.2)
Для установившегосядвижения система уравнений будет иметь вид:
ux = f1 (x, y, z);
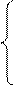
uy = f2 (x, y, z); (16.3)
uz = f3 (x, y, z).
Располагая уравнениями (16.1) и (16.2), можно определить скорость в данной точке по величине и направлению, а также ускорение j. Величина ускорения j определяется выражением:
j = 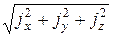 , (16.4)
, (16.4)
где проекции ускорения соответственно равны:
jx = 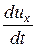 ; jy =
; jy = 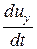 ; jz =
; jz = 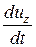 .
.
В общем случае неустановившегося движения проекции скорости ux, uy, uz являются функциями переменных Эйлера (координат x, y, z и времени t). Поэтому полный дифференциал скорости равен сумме четырёх частных дифференциалов:
dux = 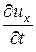 × dt +
× dt + 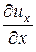 × dx +
× dx +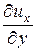 × dy +
× dy +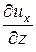 × dz,
× dz,
а её производная по времени
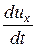 =
= 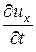 +
+ 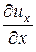 ×
× 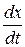 +
+ 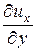 ×
× 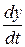 +
+ 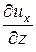 ×
× 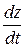 . (16.5)
. (16.5)
Рассматривая dx, dy, dz как проекции элементарного перемещения dl на оси координат, получим:
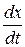 = ux;
= ux; 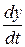 = uy;
= uy; 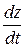 = uz.
= uz.
Тогда уравнение (16.5) запишется в виде
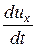 =
= 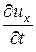 +
+ 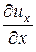 × ux +
× ux + 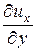 × uy +
× uy + 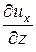 × uz.
× uz.
Аналогичные выражения можно составить также для производных 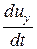 и
и 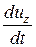 , в результате чего получим выражения для проекций ускорения в координатах Эйлера.
, в результате чего получим выражения для проекций ускорения в координатах Эйлера.
jx = 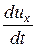 =
= 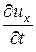 +
+ 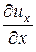 × ux +
× ux + 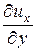 × uy +
× uy + 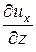 × uz.
× uz.
 jy =
jy = 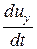 =
= 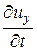 +
+  × ux +
× ux + 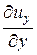 × uy +
× uy +  × uz. (16.6)
× uz. (16.6)
jz = 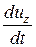 =
= 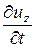 +
+ 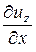 × ux +
× ux + 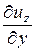 × uy +
× uy + 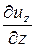 × uz.
× uz.
Полученная система получила название уравнения кинематики Эйлера или уравнения неустановившегося движения жидкости.
Уравнение потока (16.6) слагается из локальной 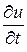 и конвективной
и конвективной 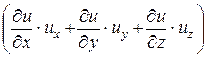 составляющих. Локальная составляющая представляет собой интенсивность изменения скорости в данной фиксированной точке пространства (при неизменных координатах x, y, z). Она обусловлена неустановившемся характером движения жидкости. Конвективная составляющая характеризует изменение скорости частицы при её перемещении относительно координатных осей – ускорение при перемещении частицы в пространстве.
составляющих. Локальная составляющая представляет собой интенсивность изменения скорости в данной фиксированной точке пространства (при неизменных координатах x, y, z). Она обусловлена неустановившемся характером движения жидкости. Конвективная составляющая характеризует изменение скорости частицы при её перемещении относительно координатных осей – ускорение при перемещении частицы в пространстве.
При установившемся движении локальная производная равна нулю
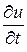 = 0.
= 0.
В случае установившегося движения уравнения имеют вид:
jx = 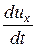 =
= 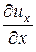 × ux +
× ux + 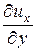 × uy +
× uy + 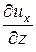 × uz.
× uz.
 jy =
jy = 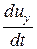 =
=  × ux +
× ux + 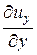 × uy +
× uy +  × uz. (16.7)
× uz. (16.7)
jz = 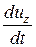 =
= 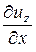 × ux +
× ux + 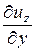 × uy +
× uy + 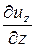 × uz.
× uz.
Тема 18 Уравнение неразрывности течения
Уравнение неразрывности течения (сплошности потока) в интегральной форме в случае одномерного приближения принимает вид уравнения постоянства расхода:
· для слобосжимаемой (или трудносжимаемой) жидкости (r = const) это уравнение постоянства объёмного расхода Q, м3/с:
Q = v × w, (18.1)
где v – средняя скорость в живом (поперечном) сечении потока, м/с;
w – площадь живого (поперечного) сечения потока, м2.
Объёмный расход потока вдоль по течению неизменен.
· для сжимаемой жидкости (r ¹ const) это уравнение постоянства массового расхода Qm, кг/с:
Qm = r × v × w, (18.2)
где r – плотность жидкости, кг/м3.
Массовый расход потока вдоль по течению неизменен.
Тема 19 Уравнение Бернулли (энергии) для элементарной струйки невязкой несжимаемой жидкости
В элементарной струйке сечениями 1-1 и 2-2 выделим некоторую массу жидкости и составим уравнение кинетической энергии (Ек) для этой массы (рис. 41).
За время dt выделенная масса жидкости переместится и займёт положение 1¢-1¢, 2¢-2¢. Рассмотрим между сечениями три объёма: (a), (b) и (c). По условиям сплошности масса объёма (a) равна массе объёма (b).
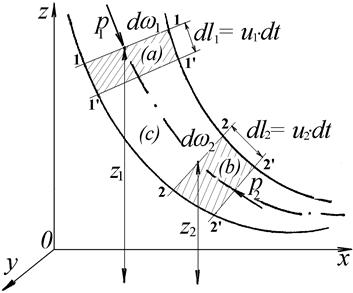
Рисунок 41
Приращение кинетической энергии 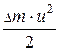 при перемещении массы жидкости из положения 1-1, 2-2 в положение 1¢-1¢, 2¢-2¢:
при перемещении массы жидкости из положения 1-1, 2-2 в положение 1¢-1¢, 2¢-2¢:
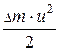 =
= 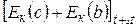 -
- 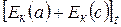 .
.
При установившемся движении кинетическая энергия массы жидкости в объёме (с) в момент времени t равна кинетической энергии массы жидкости в объёме (с) в момент времени t +D t:
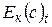 =
= 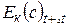
Тогда для всей выделенной массы
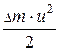 =
= 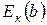 -
- 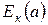 . (19.1)
. (19.1)
Кинетическая энергия массы жидкости в объёме (b) равна:
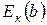 =
= 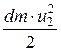 ;
;
dm = r × dw2 × dl2 = r × dw2 × u2 × dt;
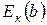 = r × dw2 × u2 × dt ×
= r × dw2 × u2 × dt × 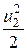 . (19.2)
. (19.2)
Аналогично, кинетическая энергия массы жидкости в объёме (а) равна:
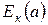 = r × dw1 × u1 × dt ×
= r × dw1 × u1 × dt × 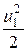 . (19.3)
. (19.3)
После подстановки (19.2) и (19.3) в выражение (19.1) получаем
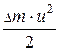 = r × dw2 × u2 × dt ×
= r × dw2 × u2 × dt × 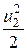 - r × dw1 × u1 × dt ×
- r × dw1 × u1 × dt × 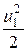 . (19.4)
. (19.4)
Для невязкой жидкости к выделенному объёму приложены силы тяжести, давления жидкости на боковую поверхность, силы давления на торцевые площадки w1 и w2.
Поскольку жидкость несжимаема, внутренняя энергия рассматриваемого объёма не меняется при его перемещении и в уравнение кинетической энергии входит только работа внешних сил.
При перемещении массы из положения 1-1, 2-2 в положение 1¢-1¢, 2¢-2¢ вес жидкости в объёме (с) работу не совершает и работу сил тяжести можно вычислить как работу перемещения из объёма (а) в (b).
Сила тяжести равна:
G = g × dm = g × r × d V = r × g × dw1 × u1 × dt.
Работа сил тяжести
G × (z1 – z2) = r × g × dw1 × u1 × dt × (z1 – z2). (19.5)
Работа сил давления на боковую поверхность равна нулю, так как эти силы нормальны к этой поверхности.
Работа сил давления на торцы равна разности:
р1 × dw1 × u1 × dt – р2 × dw2 × u2 × dt. (19.6)
Таким образом, приращение кинетической энергии (19.4) за счёт работы сил тяжести (19.5) и внешнего давления (19.6) имеет вид
r × dw2 × u2 × 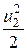 × dt - r × dw1 × u1 ×
× dt - r × dw1 × u1 × 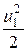 × dt =
× dt =
= r × g × dw1 × u1 × (z1 – z2) × dt + р1 × dw1 × u1 × dt – р2 × dw2 × u2 × dt.
Разделим на dt и сгруппируем
r × g × dw1 × u1 × z1 + р1 × dw1 × u1 + r × dw1 × u1 × 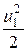 =
=
= r × g × dw1 × u1 × z2 + р2 × dw2 × u2 + r × dw2 × u2 × 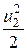 .
.
Заменим u1 × dw1 = dQ, u2 × dw2 = dQ и разделим обе части последнего уравнения на r ´ g ´ dQ.
Имеем
z1 + 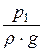 +
+ 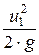 = z2 +
= z2 + 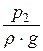 +
+ 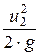 . (19.7)
. (19.7)
Это уравнение Бернулли в форме напоров для элементарной струйки между сечениями 1-1 и 2-2.
Поскольку сечения взяты произвольно, то в общем виде уравнение имеет вид:
z + 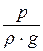 +
+ 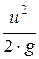 = const. (19.8)
= const. (19.8)
Каждое слагаемое в уравнении Бернулли в форме напоров имеет размерность длины (м) и представляет собой энергию, отнесённую к единице веса (1 Н), то есть удельнуюэнергию. Здесь z – удельнаяпотенциальнаяэнергияположения, 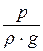 – удельнаяпотенциальнаяэнергиядавления,
– удельнаяпотенциальнаяэнергиядавления, 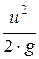 – удельнаякинетическаяэнергия.
– удельнаякинетическаяэнергия.
Уравнение Бернулли в форме давлений имеет вид:
r × g × z + р + r ×  = const. (19.9)
= const. (19.9)
Здесь каждый член имеет размерность давления (Па) и представляет собой энергию, отнесённую к единице объёма. Здесь r × g × z – гравитационноедавление, р – статическоедавление, r ×  – динамическоедавление.
– динамическоедавление.
Уравнение Бернулли имеет третью форму представления – основное уравнение Бернулли:
g × z + 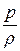 +
+  = const. (19.10)
= const. (19.10)
Каждое слагаемое в уравнении (19.10) характеризует энергию, отнесённую к единице массы (Дж/кг). При этом размерность каждого члена уравнения (м2/с2).
Тема 20 энергетический смысл и Геометрическая интерпретация уравнения Бернулли
Каждое слагаемое в уравнении Бернулли в форме напоров (19.8) имеет размерность длины (м)
z + 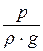 +
+ 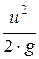 = const.
= const.
Если уравнение (19.8) умножить на 1 Н, то уравнение не изменится, но размерность каждого слагаемого будет выражена в Н´м (Дж). Следовательно, каждое слагаемое в уравнении представляет собой энергию, отнесённую к единице веса (1 Н), то есть удельнуюэнергию. Тогда
z – удельная потенциальная энергия положения;
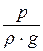 – удельная потенциальная энергия давления;
– удельная потенциальная энергия давления;
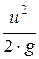 – удельная кинетическая энергия.
– удельная кинетическая энергия.
Таким образом, 1 Н жидкости, находящийся на высоте z относительно плоскости x0y может совершать работу, равную z, Дж. Тот же 1 Н жидкости, находящийся на высоте z, обладает ещё энергией давления 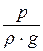 , Дж.
, Дж.
С энергетической точки зрения уравнение Бернулли можно сформулировать так:
при установившемся движении невязкой несжимаемой жидкости вдоль трубки тока сумма удельных энергий – потенциальной (положения и давления) и кинетической – есть величина постоянная.
Уравнение Бернулли показывает, что полная удельная энергия остаётся неизменной по пути данной элементарной струйки невязкой жидкости. Таким образом, уравнение Бернулли представляет собой закон сохранения механической энергии при движении идеальной жидкости.
Уравнение Бернулли в форме напоров удобно тем, что каждый член может быть представлен некоторой высотой. Так
z – геометрическая высота, то есть высота положения рассматриваемой точки пространства с жидкостью (центра тяжести сечения) над горизонтальной плоскостью сравнения x0y;
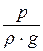 – высота давления. Если в уравнении р – избыточное давление, то величина
– высота давления. Если в уравнении р – избыточное давление, то величина
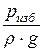 =
= 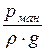 называется пьезометрической высотой;
называется пьезометрической высотой;
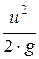 – скоростная (или динамическая) высота.
– скоростная (или динамическая) высота.
Сумма 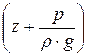 характеризует пьезометрический напор.
характеризует пьезометрический напор.
В системе координат x0y напишем уравнение Бернулли для трёх произвольных сечений элементарной струйки (рис. 42):
z1 + 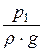 +
+ 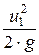 = z2 +
= z2 + 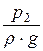 +
+ 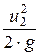 = z3 +
= z3 + 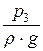 +
+ 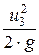 = Н = const.
= Н = const.
где Н – полная высота в данном сечении струйки.
Для каждого поперечного сечения струйки величина Н может быть представлена совокупностью отрезков z, 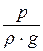 и
и 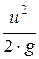 .
.
Соединив между собой концы отрезков Н, получим линию, расположенную в горизонтальной плоскости. Эту плоскость и линию на ней называют плоскостью и линией полного напора.
Соединив концы отрезков 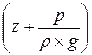 , получим пьезометрическую линию.
, получим пьезометрическую линию.
Пьезометрическая линия отделяет область изменения потенциальной энергии от области изменения кинетической энергии.
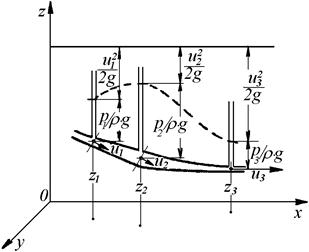
Рисунок 42 – Геометрическая интерпретация уравнения Бернулли
Рис. 42 даёт геометрическое толкование уравнения Бернулли. Можно видеть, как по длине струйки меняются слагаемые этого уравнения. Если сечение расширяется и, следовательно, скорость уменьшается, то уменьшается скоростная высота, но возрастает сумма 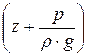 .
.
Таким образом, геометрический смысл уравнения Бернулли можно сформулировать так:
при установившемся движении невязкой несжимаемой жидкости вдоль трубки тока сумма высот – геометрической, пьезометрической и скоростной – есть величина постоянная.
Тема 21 Уравнение Бернулли для потока конечных размеров. Гидравлический и пьезометрический уклоны
Поток рассматривается как совокупность элементарных струек, движущихся с различными скоростями. В таком потоке скорости в разных точках поперечного сечения различны, а скоростной напор, определяемый средней скоростью v, дополнен коэффициентом кинетической энергии (или коэффициентом Кориолиса) a. Величина этого коэффициента отражает степень неравномерности распределения с коростей по сечению потока. Коэффициент равен отношению истинной кинетической энергии массы жидкости, протекающей через живое сечение, к кинетической энергии, вычисленной в предположении, что во всех точках живого сечения местные скорости равны средней скорости.
Обычно при прямолинейном турбулентном движении в трубах a = 1,03…1,1. Обычно при расчётах при турбулентном течении в трубах принимают коэффициент Кориолиса a равным 1,1 или 1. При прямолинейном ламинарном движении в трубах a = 2.
Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости в форме давлений имеет вид:
r × g × z + р + r × a × 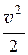 = const, (21.1, а)
= const, (21.1, а)
где r × g × z – гравитационное давление;
р – статическое давление;
r × 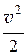 – динамическое давление.
– динамическое давление.
Для двух произвольных сечений 1-1 и 2-2 уравнение имеет вид:
r × g × z1 + р1 + r × a1 × 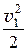 = r × g × z2 + р2 + r × a2 ×
= r × g × z2 + р2 + r × a2 × 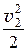 = const. (21.1, б)
= const. (21.1, б)
Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости в форме напоров имеет вид:
z + 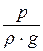 + a ×
+ a × 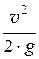 = Н = const, (21.2, а)
= Н = const, (21.2, а)
где z – удельная потенциальная энергия положения;
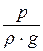 – удельная потенциальная энергия давления;
– удельная потенциальная энергия давления;
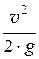 – удельная кинетическая энергия;
– удельная кинетическая энергия;
Н – полная удельная энергия потока.
Для двух произвольных сечений 1-1 и 2-2 уравнение имеет вид:
z1 + 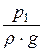 + a1 ×
+ a1 × 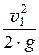 = z2 +
= z2 + 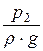 + a2 ×
+ a2 ×  = Н = const. (21.2, б)
= Н = const. (21.2, б)
С энергетической точки зрения уравнение Бернулли можно сформулировать так:
при установившемся движении невязкой несжимаемой жидкости вдоль потока сумма удельных энергий – потенциальной (положения и давления) и кинетической – есть величина постоянная.
Все члены уравнения Бернулли имеют линейную размерность и их можно интерпретировать как высоты:
z – геометрическая высота, то есть высота положения рассматриваемой точки пространства с жидкостью (центра тяжести сечения) над горизонтальной плоскостью сравнения x0y;
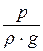 – высота давления. Если в уравнении р – избыточное давление, то величина
– высота давления. Если в уравнении р – избыточное давление, то величина
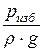 =
= 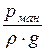 называется пьезометрической высотой;
называется пьезометрической высотой;
a × 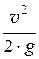 – скоростная (или динамическая) высота.
– скоростная (или динамическая) высота.
Н – полная высота в данном сечении потока.
Таким образом, геометрический смысл уравнения Бернулли можно сформулировать так:
при установившемся движении невязкой несжимаемой жидкости вдоль потока сумма высот – положения, давления ( или пьезометрической) и скоростной – есть величина постоянная.
Уравнение Бернулли для установившегося движения вязкой несжимаемой жидкости между двумя сечениями, в которых движение является плавно изменяющимся, имеет вид:
· в форме давлений
r × g × z1 + р1 + r × a1 × 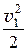 = r × g × z2 + р2 + r × a2 ×
= r × g × z2 + р2 + r × a2 × 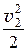 + D р, (21.3)
+ D р, (21.3)
где D р – потери давления на участке между рассматриваемыми сечениями;
· в форме напоров
z1 + 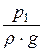 + a 1 ×
+ a 1 × 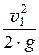 = z2 +
= z2 + 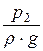 + a 2 ×
+ a 2 ×  + D hпот, (21.4)
+ D hпот, (21.4)
где D hпот – потери напора на участке между рассматриваемыми сечениями.
Для потока жидкости сумма удельной потенциальной и удельной кинетической энергии
Н = 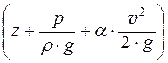 (21.5)
(21.5)
называется гидродинамическим (или полным) напором.
При движении вязкой жидкости линия удельной энергии (напорная линия) не горизонтальна, как при движении невязкой жидкости, а представляет собой наклонную линию, так как удельная энергия потока (гидродинамический напор) Е = Н = 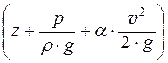 при движении вязкой жидкости уменьшается в направлении движения.
при движении вязкой жидкости уменьшается в направлении движения.
Энергетический смысл уравнения Бернулли для потока вязкой жидкости:
удельная энергия потока в предыдущем сечении всегда больше чем в последующем на величину потерь удельной энергии.
Геометрический смысл уравнения Бернулли для потока вязкой жидкости:
полная высота в предыдущем сечении всегда больше чем в последующем на высоту потерь.
Гидравлическим уклоном i называется отношение потерь напора D hтр к длине участка l, на котором эти потери происходят:
i = 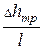 =
= 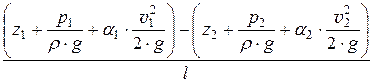 > 0. (21.6, а)
> 0. (21.6, а)
В общем виде
i = - 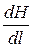 = -
= - 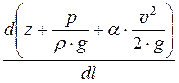 =
= 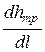 > 0. (21.6, б)
> 0. (21.6, б)
Так как приращение dH всегда является отрицательным (напор уменьшается вдоль движения), то гидравлический уклон всегда положителен.
Удельная потенциальная энергия 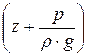 (пьезометрический напор) в направлении движения может, и уменьшатся, и увеличиваться, в зависимости от конкретных условий.
(пьезометрический напор) в направлении движения может, и уменьшатся, и увеличиваться, в зависимости от конкретных условий.
Пьезометрическим уклоном iп называется отнесённое к единице длины изменение пьезометрического напора 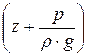 или изменение отметок пьезометрической линии. В общем случае
или изменение отметок пьезометрической линии. В общем случае
iп = - 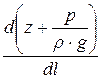 . (21.7, а)
. (21.7, а)
Для двух сечений имеем
iп = 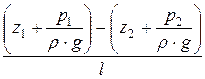 . (21.7, б)
. (21.7, б)
Пьезометрический уклон может быть положительным, отрицательным и равным нулю. Пьезометрический уклон считается положительным, если по течению пьезометрическая линия понижается.
Тема 22 ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ УРАВНЕНИЯ БЕРНУЛЛИ
Уравнение Бернулли используется во многих случаях расчёта движения жидкости в трубах, каналах и других сооружениях. На основании уравнения Бернулли сконструирован ряд приборов.
Трубка Пито-Прандтля
Рассмотрим определение местной скорости с помощью трубки Пито (рис. 43).
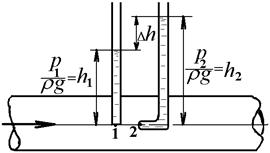
Рисунок 43 – Трубка Пито-Прандтля
Эта трубка помещена в потоке жидкости изогнутым концом против течения и работает в комплексе с пьезометром. Пьезометрическаятрубкаизмеряетстатический напор 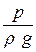 , а т рубкаПитоизмеряетполный напор - сумму статического и динамического
, а т рубкаПитоизмеряетполный напор - сумму статического и динамического 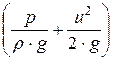 . Конструктивно объединенные в одном корпусе трубка Пито и пьезометрическая трубка (кольцевое пространство с прорезями) представляет собой трубку Пито-Прандтля. Такой прибор иногда называют гидрометрической (для капельной жидкости) или пневмометрической (для воздуха) трубкой.
. Конструктивно объединенные в одном корпусе трубка Пито и пьезометрическая трубка (кольцевое пространство с прорезями) представляет собой трубку Пито-Прандтля. Такой прибор иногда называют гидрометрической (для капельной жидкости) или пневмометрической (для воздуха) трубкой.
Проведём плоскость сравнения через центр отверстия в изогнутом конце трубки Пито и напишем уравнение Бернулли для точек 1 и 2. Это уравнение записывается для элементарной струйки, так как трубка Пито в комплекте с пьезометрической трубкой измеряет местную скорость в точке, в которой она установлена:
z1+ 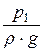 +
+  = z2 +
= z2 + 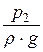 +
+ 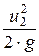 .
.
В данном случае z1 = z2, u1 = u, а u2 = 0, так как при обтекании жидкостью трубки в точке 2 происходит уменьшение скорости u до нуля и в соответствии с этим увеличение давления. Тогда
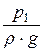 +
+ 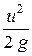 =
= 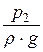 .
.
Обозначим разницу показаний в трубках Пито и пьезометрической как D h:
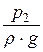 -
- 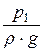 = D h.
= D h.
Уравнение Бернулли примет вид
D h = 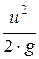 ,
,
то есть трубкаПито-Прандтляизмеряетдинамическийнапор 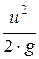 .
.
Отсюда скорость потока в данной точке равна:
u = 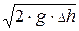 . (22.1)
. (22.1)
Если трубка Пито-Прандтля установлена на оси потока, то она измеряет максимальную скорость:
umax = 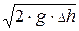 . (22.2)
. (22.2)
Чтобы трубкой Пито-Прандтля можно было непосредственно измерять скорость, к ней подключается дифференциальный манометр (в ряде случаев микроманометр).
Трубка Пито-Прандтля выполняется небольшим диаметром и с обтекаемым носком, но и в этом случае она вносит некоторое возмущение в поток. Поэтому полученное значение скорости по формулам (22.1) или (22.2) умножают на тарировочный коэффициент, определяемый опытным путём. Для заводских трубок тарировочный коэффициент равен 1…1,04.
Водомер Вентури
Расход в трубопроводе можно измерить с помощью водомера Вентури, представляющего собой вставку меньшего диаметра с плавным входом и выходом (рис.44).
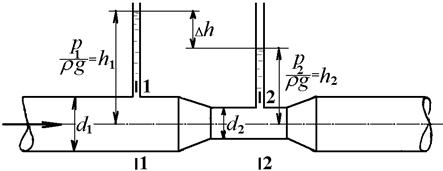
Рисунок 44 – Водомер Вентури
В суженной части диаметром d 2 скорость увеличивается, а давление и пьезометрическая высота 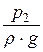 = h2 уменьшаются по сравнению с давлением и пьезометрической высотой до сужения
= h2 уменьшаются по сравнению с давлением и пьезометрической высотой до сужения 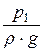 = h1. Зависимость между объёмным расходом Q и разностью h1 - h2 = D h можно получить с помощью уравнения Бернулли и уравнения расхода. Расчётные сечения выберем до сужения 1-1 и в суженной части 2-2. Ввиду небольшого расстояния между сечениями и плавного сужения потери напора D hпот между этими сечениями будут незначительными и в первом приближении ими можно пренебречь. Если труба горизонтальна, то z 1 = z 2 и уравнение Бернулли примет вид
= h1. Зависимость между объёмным расходом Q и разностью h1 - h2 = D h можно получить с помощью уравнения Бернулли и уравнения расхода. Расчётные сечения выберем до сужения 1-1 и в суженной части 2-2. Ввиду небольшого расстояния между сечениями и плавного сужения потери напора D hпот между этими сечениями будут незначительными и в первом приближении ими можно пренебречь. Если труба горизонтальна, то z 1 = z 2 и уравнение Бернулли примет вид
h1 + a1 ×  = h2 + a2 ×
= h2 + a2 × 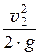 .
.
С учетом того, что средняя скорость в сечении v из уравнения неразрывности течения равна отношению расхода Q к площади живого сечения потока w (v = 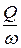 ) и, принимая a1 = a2 = 1, получим:
) и, принимая a1 = a2 = 1, получим:
h 1 - h 2 = 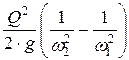 .
.
Для круглой трубы w = 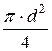 и тогда расход можно вычислить по формуле:
и тогда расход можно вычислить по формуле:
Q = 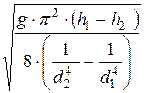 =
= 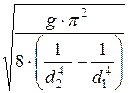 ×
× 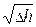 = B ×
= B × 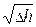 ,
,
где В – постоянная величина для каждого водомера.
В = 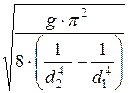 =
= 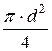 ×
× 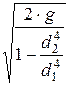 .
.
Фактический расход Qф будет несколько меньше из-за потерь напора:
Qф = m × Q,
где m = тарировочный коэффициент (коэффициент расхода), значение которого меньше единицы. Обычно m = 0,95…0,97.
Тема 24 Ламинарный и турбулентный режимы движения жидкости. Число Рейнольдса и его критическое значение
Потери энергии при движении жидкости зависят от режима движения жидкости.
При небольших значениях скорости v жидкость движется отдельными не перемешивающимися слоями (рис. 46, а).
Движение жидкости, при котором отсутствуют изменения (пульсации) местных скоростей, приводящие к перемешиванию жидкости, называют ламинарным (от латинского слова lamina – слой, пластинка).
Движение жидкости, при котором происходят изменения (пульсации) местных скоростей, приводящие к перемешиванию жидкости называют турбулентным (от латинского слова turbulentus – беспорядочный, бурный).
Рейнольдс установил, что переход от ламинарного течения к турбулентному и наоборот определяется средней скоростью течения v, характерным поперечным размером потока L, физическими свойствами жидкости: плотностью r и вязкостью (динамический коэффициент вязкости h или кинематический коэффициент вязкости n). В общем случае режим движения жидкости определяется безразмерным комплексом, составленным из указанных величин и называемым числом (критерием) Рейнольдса
Re =  =
= 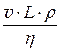 (24.1)
(24.1)
Число Рейнольдса характеризует отношение сил инерции к силам трения (вязкости).
Переход от одного режима движения в другой объясняется преобладанием силы инерции или силы трения.
В качестве характерного геометрического размера живого сечения потока L чаще всего принимают диаметр трубы d (для круглых напорных труб), для некруглых и безнапорных труб гидравлический радиус R или диаметр эквивалентный 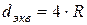 . Тогда, соответственно
. Тогда, соответственно
Re = 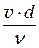 ,
, 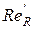 =
= 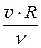 , Red экв =
, Red экв = 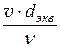
Скорость потока, при которой происходит смена режима движения жидкости, называется критической. Рейнольдс обнаружил существование двух критических скоростей: верхней критической скорости – при переходе ламинарного режима движения в турбулентный, и нижней критической скорости – при переходе турбулентного режима движения в ламинарный. Соответственно различают верхнее и нижнее критические числа Рейнольдса.
| Ламинарный режим | Возможен устойчивый | Возможен неустойчивый | Невозможен |
| Турбулентный режим | Невозможен | Возможен устойчивый | Возможен устойчивый |
0 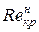
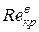 Re
Re
Для круглых напорных труб при установившемся равномерном движении жидкости 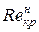 = 2000 … 2320, а
= 2000 … 2320, а 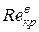 = 4000 … 100000.
= 4000 … 100000.
Значение 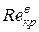 (переход ламинарного течения в турбулентное) зависит от внешних условий опыта: постоянства температуры, уровня вибрации установки, условий входа в трубку, шероховатости поверхности стенок трубы, состояния жидкости в резервуаре, питающем трубу и т.п. Значение
(переход ламинарного течения в турбулентное) зависит от внешних условий опыта: постоянства температуры, уровня вибрации установки, условий входа в трубку, шероховатости поверхности стенок трубы, состояния жидкости в резервуаре, питающем трубу и т.п. Значение 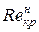 (переход турбулентного движения в ламинарное) от этих величин практически не зависит.
(переход турбулентного движения в ламинарное) от этих величин практически не зависит.
При Re < 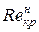 будет существовать ламинарное (слоистое) движение, причём оно будет устойчиво, то есть искусственно разрушить слоистую структуру (турбулизовать поток), то она восстановится. При больших числах Re >
будет существовать ламинарное (слоистое) движение, причём оно будет устойчиво, то есть искусственно разрушить слоистую структуру (турбулизовать поток), то она восстановится. При больших числах Re > 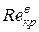 слоистая структура существовать не может. А в диапазоне
слоистая структура существовать не может. А в диапазоне 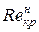 < Re <
< Re < 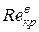 ламинарный режим существовать может, но он неустойчив; если слоистая структура разрушается, то вновь она не восстанавливается и режим движения становится турбулентным. Достаточно воздействия малого возмущения, чтобы произошёл переход в турбулентное движение. В практических условиях, где всегда есть источники случайных возмущений, следует считаться только с нижней границей.
ламинарный режим существовать может, но он неустойчив; если слоистая структура разрушается, то вновь она не восстанавливается и режим движения становится турбулентным. Достаточно воздействия малого возмущения, чтобы произошёл переход в турбулентное движение. В практических условиях, где всегда есть источники случайных возмущений, следует считаться только с нижней границей.
Таким образом, в качестве критического числа Рейнольдса принят 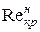 для цилиндрических напорных труб
для цилиндрических напорных труб
Reкр = 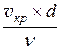 = 2000…2320.
= 2000…2320.
Для любого потока по известным v, L и n можно вычислить число Рейнольдса и сравнить его с критическим значением Reкр. Если Re < Reкр, то v < 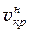 и режим движения жидкости ламинарный; если Re > Reкр, то v >
и режим движения жидкости ламинарный; если Re > Reкр, то v > 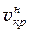 и режим движения турбулентный.
и режим движения турбулентный.
В природе и технике турбулентное движение жидкости наблюдается чаще, чем ламинарное. Области ламинарного движения:
· движение очень вязких жидкостей типа масел по трубам и механизмам;
· движение грунтовых вод (но оно может быть также и турбулентным);
· движение в капиллярах (в том числе и движение крови в живых организмах).
Тема 25 Основные отличия ламинарного и турбулентного движения в трубе круглого сечения
При ламинарном движении жидкость движется отдельными, не перемешивающимися слоями.
При турбулентном течении поток несжимаемой жидкости может быть разделён на пограничный вязкий подслой и основную часть потока – турбулентное ядро, с соответствующими преобладающими видами вязкости.
Турбулентный поток по своим свойствам резко отличается от ламинарного. Пульсации векторов местных скоростей в турбулентном потоке влияют на соответствующие потери энергии, входящие в уравнение Бернулли. В результате турбулентного перемешивания величина потерь энергии возрастает и зависит не только от вязкостных свойств, как в случае ламинарного течения, но и от степени турбулизации. При ламинарном режиме потери энергии подлине пропорциональны средней скорости потока v в первой степени, при турбулентном – скорости в степени 1,75…2.
Отличны процессы передачи тепла при ламинарном и турбулентном режимах течения. В первом случае теплообмен происходит только за счёт теплопроводности жидкости; при турбулентном режиме в результате непрерывного поперечного перемещения частиц решающую роль играет теплообмен путём конвекции. Поэтому эффективность теплообмена при турбулентном режиме намного больше, чем при ламинарном.
Наконец, вопрос о двух режимах течения тесно связан с эффектом турбулентной диффузии, когда поперечные перемещения масс жидкости способствуют переносу твёрдых частиц.
Основные отличия ламинарного и турбулентного режима течения, в случае движения в круглом напорном трубопроводе представлены в таблице 23.1.
Таблица 23.1 – Основные отличия ламинарного и турбулентного течения (движение в трубе круглого сечения)
| Признак | Ламинарный режим | Турбулентный режим | |||||
| Число Рейнольдса | Re < Reкр | Re > Reкр | |||||
| Структура потока | Жидкость движется отдельными не перемешивающимися между собой слоями
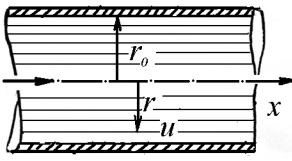 Рисунок 47 – Структура потока при ламинарном движении
Рисунок 47 – Структура потока при ламинарном движении
| Структура потока может быть представлена в виде приближенной двухслойной модели (схемы).
Вблизи твердой стенки находится очень тонкий (его толщина 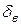 около 0,01 радиуса трубы около 0,01 радиуса трубы 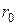 ) вязкий подслой, где преобладают силы вязкости. Основная часть потока – турбулентное ядро, где происходят интенсивные пульсации скорости и перемешивание частиц жидкости ) вязкий подслой, где преобладают силы вязкости. Основная часть потока – турбулентное ядро, где происходят интенсивные пульсации скорости и перемешивание частиц жидкости
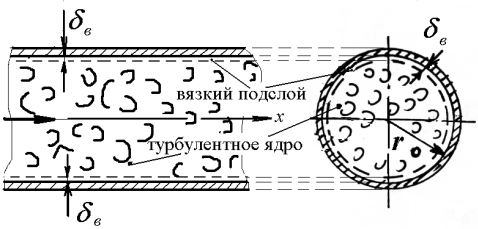 Рисунок 48 – Структура потока при турбулентном режиме движения жидкости
Рисунок 48 – Структура потока при турбулентном режиме движения жидкости
| |||||
| Касательные напряжения | Касательные напряжения зависят только от вязкостных свойств жидкости. Рассчитываются по закону вязкого трения Ньютона
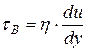 где
где 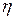 – динамический коэффициент вязкости. Учитывает молекулярную структуру жидкости. – динамический коэффициент вязкости. Учитывает молекулярную структуру жидкости.
| Возникают дополнительные касательные напряжения, вызванные пульсацией потока  , которые должны быть добавлены к вязкостным: , которые должны быть добавлены к вязкостным:
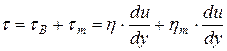 где
где | |||||
|
Дата добавления: 2014-01-04; Просмотров: 1445; Нарушение авторских прав?; Мы поможем в написании вашей работы!