Методические указания к решению задач. Применяя формулы числа перестановок, сочетаний и размещений, следует исходить из определений этих понятий

Применяя формулы числа перестановок, сочетаний и размещений, следует исходить из определений этих понятий.

Пример 7. Задано множество .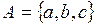

1. Составить всевозможные перестановки этого множества.

2. Всевозможные сочетания по два элемента.

3. Всевозможные размещения по два элемента.

Решение:

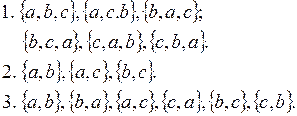
Пример 8. Сколько существует способов выбора из 7 человек комиссии, состоящей из 3 человек?

Решение. Число возможных составов комиссии равно числу всевозможных трехэлементных подмножеств множества, состоящего из 7 человек, т.е.

Пример 9. Сколькими способами можно разместить на полке 4 книги?

Решение. Искомое число способов равно числу способов упорядочения множества, состоящего из 4 элементов, т.е.

Пример 10. В студенческой группе 25 человек. Надо выбрать старосту группы, академорга и профорга. Сколькими способами может быть сделан выбор, если каждый член группы может занимать только один пост?

Решение. В данном примере из множества в 25 элементов нужно выбрать 3 элемента, но среди выбранных 3 элементов имеет значение порядок, так как здесь играет роль то, кто какой пост займет.

Например, выбор:

староста – Иванова, академорг – Алексеева, профорг – Петров отличается от выбора:

староста – Алексеева, академорг – Иванова, профорг – Петров.

Следовательно, число различных способов выбора равно числу размещений из 25 элементов по 3,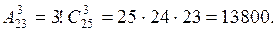

Пример 11. На профсоюзном собрании присутствует 50 человек. Необходимо выбрать делегацию из 5 человек на профсоюзную конференцию. Сколькими способами это можно сделать?

Решение. В данном примере из множества в 50 элементов нужно выбрать подмножество из 5, порядок которых не играет роли. Поэтому число способов выбора делегации равно

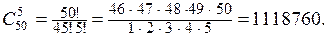
Пример 12. Сколькими способами можно упорядочить множество так, чтобы каждое четное число имело четный номер?

Решение. Здесь можно рассматривать 2 объекта: четные и нечетные числа.

Мест с четными номерами n. Таким образом, четные числа можно расставить n! способами. Общее число искомых перестановок по правилу умножения равно

Дата добавления: 2014-01-04