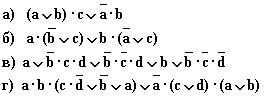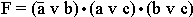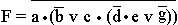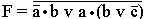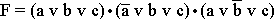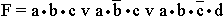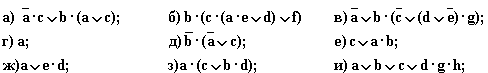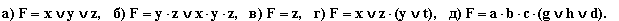КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
II. Решение логических задач табличным способом
|
|
|
|
При использовании этого способа условия, которые содержит задача, и результаты рассуждений фиксируются с помощью специально составленных таблиц.
Пример 3. В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
Известно, что:
1. Смит самый высокий;
2. играющий на скрипке меньше ростом играющего на флейте;
3. играющие на скрипке и флейте и Браун любят пиццу;
4. когда между альтистом и трубачом возникает ссора, Смит мирит их;
5. Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как музыкантов трoе, инструментов шесть и каждый владеет только двумя инструментами, получается, что каждый музыкант играет на инструментах, которыми остальные не владеют.
Из условия 4 следует, что Смит не играет ни на альте, ни на трубе, а из условий 3 и 5, что Браун не умеет играть на скрипке, флейте, трубе и гобое. Следовательно, инструменты Брауна — альт и кларнет. Занесем это в таблицу, а оставшиеся клетки столбцов "альт" и "кларнет" заполним нулями:
| скрипка | флейта | альт | кларнет | гобой | труба | |
| Браун | ||||||
| Смит | ||||||
| Вессон |
Из таблицы видно, что на трубе может играть только Вессон.
Из условий 1 и 2 следует, что Смит не скрипач. Так как на скрипке не играет ни Браун, ни Смит, то скрипачом является Вессон. Оба инструмента, на которых играет Вессон, теперь определены, поэтому остальные клетки строки "Вессон" можно заполнить нулями:
| скрипка | флейта | альт | кларнет | гобой | труба | |
| Браун | ||||||
| Смит | ||||||
| Вессон |
Из таблицы видно, что играть на флейте и на гобое может только Смит.
| скрипка | флейта | альт | кларнет | гобой | труба | |
| Браун | ||||||
| Смит | ||||||
| Вессон |
Ответ: Браун играет на альте и кларнете, Смит — на флейте и гобое, Вессон — на скрипке и трубе.
Пример 4. Три одноклассника — Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби.
Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги.
Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия.
Решение. Здесь исходные данные разбиваются на тройки (имя — профессия — увлечение).
Из слов Юры ясно, что он не увлекается туризмом и он не врач. Из слов врача следует, что он турист.
| Имя | Юра | ||
| Профессия | врач | ||
| Увлечение | туризм |
Буква "а", присутствующая в слове "врач", указывает на то, что Влад тоже не врач, следовательно врач — Тимур. В его имени есть буквы "т" и "р", встречающиеся в слове "туризм", следовательно второй из друзей, в названиях профессии и увлечения которого не встречается ни одна буква его имени — Юра. Юра не юрист и не регбист, так как в его имени содержатся буквы "ю" и "р". Следовательно, окончательно имеем:
| Имя | Юра | Тимур | Влад |
| Профессия | физик | врач | юрист |
| Увлечение | бег | туризм | регби |
Ответ. Влад — юрист и регбист, Тимур — врач и турист, Юра — физик и бегун.
Пример 5. Три дочери писательницы Дорис Кей — Джуди, Айрис и Линда, тоже очень талантливы. Они приобрели известность в разных видах искусств — пении, балете и кино. Все они живут в разных городах, поэтому Дорис часто звонит им в Париж, Рим и Чикаго.
Известно, что:
1. Джуди живет не в Париже, а Линда — не в Риме;
2. парижанка не снимается в кино;
3. та, кто живет в Риме, певица;
4. Линда равнодушна к балету.
Где живет Айрис, и какова ее профессия?
Решение. Составим таблицу и отразим в ней условия 1 и 4, заполнив клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание:
| Париж | Рим | Чикаго | Пение | Балет | Кино | |
| Джуди | ||||||
| Айрис | ||||||
| Линда |
Далее рассуждаем следующим образом. Так как Линда живет не в Риме, то, согласно условию 3, она не певица. В клетку, соответствующую строке "Линда" и столбцу "Пение", ставим 0.
Из таблицы сразу видно, что Линда киноактриса, а Джуди и Айрис не снимаются в кино.
| Париж | Рим | Чикаго | Пение | Балет | Кино | |
| Джуди | ||||||
| Айрис | ||||||
| Линда |
Согласно условию 2, парижанка не снимается в кино, следовательно, Линда живет не в Париже. Но она живет и не в Риме. Следовательно, Линда живет в Чикаго. Так как Линда и Джуди живут не в Париже, там живет Айрис. Джуди живет в Риме и, согласно условию 3, является певицей. А так как Линда киноактриса, то Айрис балерина.
В результате постепенного заполнения получаем следующую таблицу:
| Париж | Рим | Чикаго | Пение | Балет | Кино | |
| Джуди | ||||||
| Айрис | ||||||
| Линда |
Ответ. Айрис балерина. Она живет в Париже.
III. Решение логических задач с помощью рассуждений
Этим способом обычно решают несложные логические задачи.
Пример 6. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Решение. Имеется три утверждения:
1. Вадим изучает китайский;
2. Сергей не изучает китайский;
3. Михаил не изучает арабский.
Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно.
Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно.
Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.
Пример 7. В поездке пятеро друзей — Антон, Борис, Вадим, Дима и Гриша, знакомились с попутчицей. Они предложили ей отгадать их фамилии, причём каждый из них высказал одно истинное и одно ложное утверждение:
Дима сказал: "Моя фамилия — Молотов, а фамилия Бориса — Хрущев". Антон сказал: "Молотов — это моя фамилия, а фамилия Вадима — Брежнев". Борис сказал: "Фамилия Вадима — Тихонов, а моя фамилия — Молотов". Вадим сказал: "Моя фамилия — Брежнев, а фамилия Гриши — Чехов". Гриша сказал: "Да, моя фамилия Чехов, а фамилия Антона — Тихонов".
Какую фамилию носит каждый из друзей?
Решение. Обозначим высказывательную форму "юноша по имени А носит фамилию Б" как АБ, где буквы А и Б соответствуют начальным буквам имени и фамилии.
Зафиксируем высказывания каждого из друзей:
1. ДМ и БХ;
2. АМ и ВБ;
3. ВТ и БМ;
4. ВБ и ГЧ;
5. ГЧ и АТ.
Допустим сначала, что истинно ДМ. Но, если истинно ДМ, то у Антона и у Бориса должны быть другие фамилии, значит АМ и БМ ложно. Но если АМ и БМ ложны, то должны быть истинны ВБ и ВТ, но ВБ и ВТ одновременно истинными быть не могут.
Значит остается другой случай: истинно БХ. Этот случай приводит к цепочке умозаключений: БХ истинно ® БМ ложно ® ВТ истинно ® АТ ложно ® ГЧ истинно ® ВБ ложно ® АМ истинно.
Ответ: Борис — Хрущев, Вадим — Тихонов, Гриша — Чехов, Антон — Молотов, Дима — Брежнев.
Пример 8. Министры иностранных дел России, США и Китая обсудили за закрытыми дверями проекты соглашения о полном разоружении, представленные каждой из стран. Отвечая затем на вопрос журналистов: "Чей именно проект был принят?", министры дали такие ответы:
Россия — "Проект не наш, проект не США";
США — "Проект не России, проект Китая";
Китай — "Проект не наш, проект России".
Один из них (самый откровенный) оба раза говорил правду; второй (самый скрытный) оба раза говорил неправду, третий (осторожный) один раз сказал правду, а другой раз — неправду.
Определите, представителями каких стран являются откровенный, скрытный и осторожный министры.
Решение. Для удобства записи пронумеруем высказывания дипломатов:
Россия — "Проект не наш" (1), "Проект не США" (2);
США — "Проект не России" (3), "Проект Китая" (4);
Китай — "Проект не наш" (5), "Проект России" (6).
Узнаем, кто из министров самый откровенный.
Если это российский министр, то из справедливости (1) и (2) следует, что победил китайский проект. Но тогда оба утверждения министра США тоже справедливы, чего не может быть по условию.
Если самый откровенный — министр США, то тогда вновь получаем, что победил китайский проект, значит оба утверждения российского министра тоже верны, чего не может быть по условию.
Получается, что наиболее откровенным был китайский министр. Действительно, из того, что (5) и (6) справедливы, cледует, что победил российский проект. А тогда получается, что из двух утверждений российского министра первое ложно, а второе верно. Оба же утверждения министра США неверны.
Ответ: Откровеннее был китайский министр, осторожнее — российский, скрытнее — министр США.
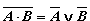 , что соответствует высказывательной форме “это утро не ясное или оно не не теплое ”; и) “число n не делится на 2 и оно делится на 3”; к) “этот треугольник не равнобедренный или он не прямоугольный”; л) “не каждый ученик писал контрольную своей ручкой” (вариант: "кто-то писал контрольную не своей ручкой").
5.5. Определите, какие из высказываний (высказывательных форм) в следующих парах являются отрицаниями друг друга, а какие нет:
, что соответствует высказывательной форме “это утро не ясное или оно не не теплое ”; и) “число n не делится на 2 и оно делится на 3”; к) “этот треугольник не равнобедренный или он не прямоугольный”; л) “не каждый ученик писал контрольную своей ручкой” (вариант: "кто-то писал контрольную не своей ручкой").
5.5. Определите, какие из высказываний (высказывательных форм) в следующих парах являются отрицаниями друг друга, а какие нет:
 .
5.9. Формализуйте предостережение, которое одна жительница древних Афин сделала своему сыну, собиравшемуся заняться политической деятельностью: “ Если ты будешь говорить правду, то тебя возненавидят люди. Если ты будешь лгать, то тебя возненавидят боги. Но ты должен говорить правду или лгать. Значит, тебя возненавидят люди или возненавидят боги ”.
Формализуйте также ответ сына: “ Если я буду говорить правду, то боги будут любить меня. Если я буду лгать, то люди будут любить меня. Но я должен говорить правду или лгать. Значит, меня будут любить боги или меня будут любить люди ”. [ Ответ ] 5.9. Решение. Введем обозначения для логических высказываний: а – “ты будешь говорить правду”; b – “тебя возненавидят люди”; c – “тебя возненавидят боги”. Договоримся считать, что некоторое заданное высказывание x истинно, если нет оговорки. Тогда предостережение матери можно записать так:
.
5.9. Формализуйте предостережение, которое одна жительница древних Афин сделала своему сыну, собиравшемуся заняться политической деятельностью: “ Если ты будешь говорить правду, то тебя возненавидят люди. Если ты будешь лгать, то тебя возненавидят боги. Но ты должен говорить правду или лгать. Значит, тебя возненавидят люди или возненавидят боги ”.
Формализуйте также ответ сына: “ Если я буду говорить правду, то боги будут любить меня. Если я буду лгать, то люди будут любить меня. Но я должен говорить правду или лгать. Значит, меня будут любить боги или меня будут любить люди ”. [ Ответ ] 5.9. Решение. Введем обозначения для логических высказываний: а – “ты будешь говорить правду”; b – “тебя возненавидят люди”; c – “тебя возненавидят боги”. Договоримся считать, что некоторое заданное высказывание x истинно, если нет оговорки. Тогда предостережение матери можно записать так: 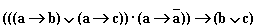 . А ответ сына – так:
. А ответ сына – так:  .
5.10. Пусть a = “ это утро ясное ”, а b = “ это утро теплое ”. Выразите следующие формулы на обычном языке:
.
5.10. Пусть a = “ это утро ясное ”, а b = “ это утро теплое ”. Выразите следующие формулы на обычном языке:  [[ Ответ ] 5.10.
[[ Ответ ] 5.10.
 ; б)
; б)  .
.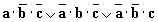 .
.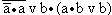






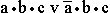


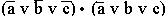
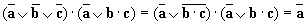 .
. 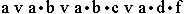
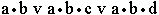

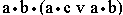
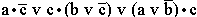
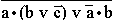
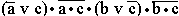


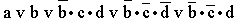
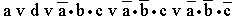


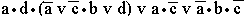
 ; в)
; в)  ; г) a v c; д) a•(c v b•d); е)
; г) a v c; д) a•(c v b•d); е)  ; ж)
; ж)  ; з)
; з)  ; и) a•(b v c•d); к)
; и) a•(b v c•d); к) 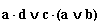 .
.





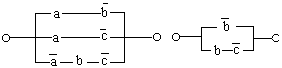

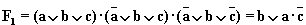 ;
; 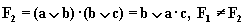 ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
.