
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нулевой метод
|
|
|
|
Метр
эталона метра длины, равной 1 650763,73 длины волны и вакууме излучения, соответствующего переходу между уровнями 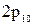 и
и 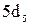 атома криптона-86 (криптоновый метр). Этот эталон мог воспроизводиться в отдельных метрологических лабораториях, точность его по сравнению с платиноиридиевым прототипом была на порядок выше.
атома криптона-86 (криптоновый метр). Этот эталон мог воспроизводиться в отдельных метрологических лабораториях, точность его по сравнению с платиноиридиевым прототипом была на порядок выше.
За эталон метра в 1983 г. было принято расстояние, проходимое светом в вакууме за 1/299 792 458 долю секунды.
килограмм.
Государственный первичный эталон и государственная поверочная схема для средств измерения массы определяются ГОСТ 8.021-84.
В области термодинамических величин действуют:
― два первичных и один специальный эталоны, воспроизводящие единицу температуры — Кельвин в различных диапазонах;
― 11 государственных эталонов теплофизики – количества теплоты, удельной теплоемкости, теплопроводности и др.
Погрешность воспроизведения точки кипения воды составляет , точки таяния льда –
, точки таяния льда – . Тройная точка воды, являющаяся точкой равновесия воды в твердой, жидкой и газообразной фазах, может быть воспроизведена в специальных сосудах с погрешностью не более 0,0002°С. В 1954 г. было принято решение о переходе к определению термодинамической температуры T по одной реперной точке – тройной точке воды, равной 273,16 К. Таким образом, единицей термодинамической температуры служит Кельвин, определяемый как 1/273,16 части тройной точки воды. Температура в градусах Цельсия t определяется как t = Т- 273,16 К. Единицей в этом случае является градус Цельсия, который равен Кельвину.
. Тройная точка воды, являющаяся точкой равновесия воды в твердой, жидкой и газообразной фазах, может быть воспроизведена в специальных сосудах с погрешностью не более 0,0002°С. В 1954 г. было принято решение о переходе к определению термодинамической температуры T по одной реперной точке – тройной точке воды, равной 273,16 К. Таким образом, единицей термодинамической температуры служит Кельвин, определяемый как 1/273,16 части тройной точки воды. Температура в градусах Цельсия t определяется как t = Т- 273,16 К. Единицей в этом случае является градус Цельсия, который равен Кельвину.
Государственная поверочная схема для средств измерения температуры устанавливается ГОСТ 8.558 – 93.
ампер
Государственный первичный эталон ампера состоит из аппаратуры включающей меру напряжения, меру электрического сопротивления, сверхпроводящий компаратор тока и регулируемые источники тока (ГОСТ 8.027-89, ГОСТ 8.022-91).
В 1979 г. на XVI Генеральной конференции мер и весов было принято новое определение, по которому канделла воспроизводится путем косвенных измерений. В России единство измерений световых величин обеспечивает ГОСТ 8.023– 90.
Современный государственный эталон канделлы имеет диапазон номинальных значений 30-110 кд, среднее квадратическое отклонение результата измерений – 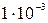 кд; не исключенная систематическая погрешность составляет
кд; не исключенная систематическая погрешность составляет кд.
кд.
Государственный первичный эталон и государственная поверочная схема для измерения плоского угла устанавливаются ГОСТ 8.016—81. Первичный эталон обеспечивает воспроизведение градуса с неисключенной погрешностью не более 0,02".
. Основы техники измерений параметров технических систем
. Модель измерения и основные постулаты метрологии
 х у у, z
х у у, z
zi zL
Рис. 2.1. Модель измерения.
плотность вероятности 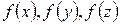 .
.
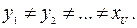
Под истинным значением физической величины понимается значение, которое идеальным образом отражало бы в качественном и количественном отношениях соответствующие свойства ТС через ее выходной параметр.
хд,
Изложенное позволяет сформулировать основные постулаты метрологии.
― Истинное значение определяемой величины существует, и оно постоянно.
― Истинное значение измеряемой величины отыскать невозможно. Отсюда следует, что результат измерения у, как правило, математически связан с измеряемой величиной вероятностной зависимостью.
Контроль – частный случай измерения, и он проводится с целью установления соответствия измеряемой величины заданному допуску. Контроль используется также для настройки, регулировки и при установке (замене) отдельных блоков ТС.
Более сложной метрологической операцией является испытание, которое состоит в воспроизведении в заданной последовательности определенных воздействий, измерении реакций объекта на данное воздействие и регистрации этих реакций.
Диагностирование системы – это процесс распознавания состояния элементов этой системы в данный момент времени. По результатам диагностирования можно прогнозировать состояние элементов системы при дальнейшей ее эксплуатации.
Виды и методы измерений.
Классификация видов измерений приведена на рис. 2.2.
Уравнение прямого измерения: у = Сх, где С — цена деления СИ.
Уравнение косвенного измерения , где х – i -й результат прямого измерения.
, где х – i -й результат прямого измерения.
Совокупные измерения
При определении взаимоиндуктивности катушки М, например, используют два метода: сложения и вычитания полей. Если индуктивность одной из них 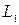 , а другой–
, а другой– , то находят
, то находят  и
и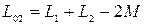 . Откуда
. Откуда  .
.
Совместными называют производимые одновременно (прямые и косвенные) измерения двух или нескольких неодноименных величин.
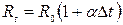 ,
,
где  и
и  сопротивление при известной температуре tо (обычно 20 °С) и температурный коэффициент — величины постоянные, измеренные косвенным методом;
сопротивление при известной температуре tо (обычно 20 °С) и температурный коэффициент — величины постоянные, измеренные косвенным методом; 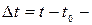 разность температур; t – заданное значение температуры, измеряемое прямым методом.
разность температур; t – заданное значение температуры, измеряемое прямым методом.
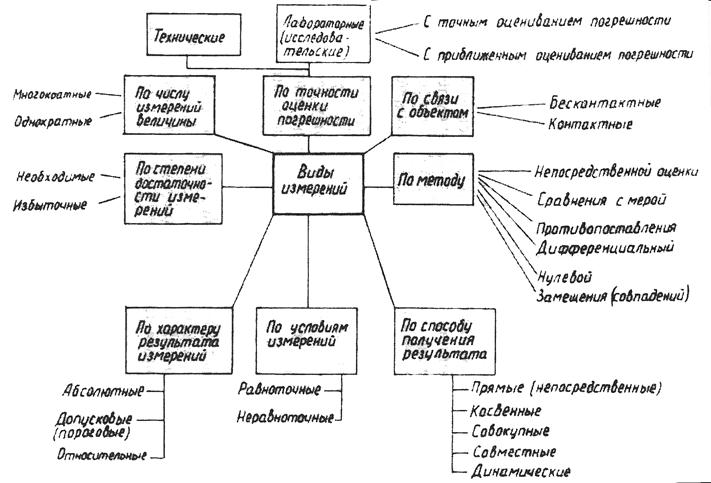 Рис. 2.2. Классификация видов измерений.
Рис. 2.2. Классификация видов измерений.
Методика – это технология выполнения измерений с целью наилучшей реализации метода.
Прямые измерения – основа более сложных измерений, и поэтому целесообразно рассмотреть методы прямых измерений. В соответствии с РМГ 29–99 различают:
1. Метод непосредственной оценки, при котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора, например измерение давления пружинным манометром, массы — на весах, силы электрического тока – амперметром.
2. Метод сравнения с мерой, где измеряемую величину сравнивают с величиной, воспроизводимой мерой. Например, измерение массы на рычажных весах с уравновешиванием гирей; измерение напряжения постоянного тока на компенсаторе сравнением с ЭДС параллельного элемента.
3. Метод дополнения, если значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.
4. Дифференциальный метод характеризуется измерением разности между измеряемой величиной и известной величиной, воспроизводимой мерой. Метод позволяет получить результат высокой точности при использовании относительно грубых средств измерения.
Пример 2.1. Измерить длину х стержня, если известна длина l (l < х) меры. Как показано на рис. 2.3, х= 1+ а (а— измеряемая величина). Действительные значения aд будут отличаться от измеренного а на величину погрешности 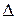 :
:
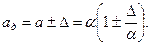
Тогда
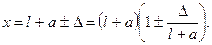
Поскольку 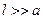 , то
, то 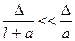 .
.
Пусть Δ= 0,1 мм; l = 1000 мм; а = 10 мм. Тогда
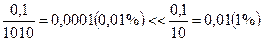 .
.

. Рис. 2.3. Дифференциальный метод измерения.
 .
.
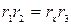 ,
,
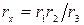 .
.

Рис. 2.4. Нулевой метод измерения:
а – схема механических весов; б –схема электрического моста.
6. Метод замещения –
нестандартизованные методы:
2.3. Погрешности измерений.

Рис. 2.5. Классификация погрешностей измерения.
Погрешность измерения Δхизм –
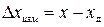 .
.
Абсолютная погрешность определяется как разность  или
или 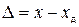 , а относительная – как отношение
, а относительная – как отношение
 или
или  .
.
Приведенная погрешность , где
, где  нормированное значение величины. Например,
нормированное значение величины. Например, 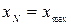 , где
, где 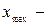 максимальное значение измеряемой величины.
максимальное значение измеряемой величины.
 (2.1)
(2.1)
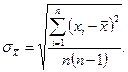 (2.2)
(2.2)
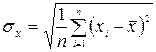 при п >20
при п >20
или (2.3)
 при п < 20.
при п < 20.
Формулы (2.2) и (2.3) соответствуют центральной предельной теореме теории вероятностей, согласно которой
 . (2.4)
. (2.4)
Нужно четко разграничивать применение 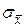 и
и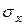
Систематическая 
Случайная 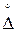
Грубые погрешности (промахи)
 или через СКО
или через СКО  .
.
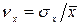 или
или 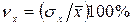 . (2.5)
. (2.5)
 < 0,33,...,0,35
< 0,33,...,0,35
Если Р означает вероятность 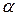 того, что
того, что 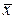 результата измерения отличается от истинного на величину не более чем
результата измерения отличается от истинного на величину не более чем 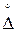 , т. е.
, т. е.
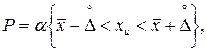 (2.6)
(2.6)
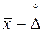 до
до 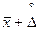 – доверительный интервал.
– доверительный интервал.
Например: при  значение Р = 0,68; при
значение Р = 0,68; при 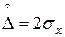 значение Р= 0,95; при
значение Р= 0,95; при 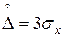 значение Р =0,99.
значение Р =0,99.

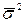 . Причем
. Причем 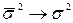 лишь при
лишь при  . То есть если считать, что
. То есть если считать, что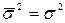 , то надежность оценки уменьшается с уменьшением п, а значения доверительной вероятности Р завышаются.
, то надежность оценки уменьшается с уменьшением п, а значения доверительной вероятности Р завышаются.
коэффициент Стьюдента  ,
,
 и отличается от действительного значения на относительную величину
и отличается от действительного значения на относительную величину  .
.
Если систематическая погрешность определяется классом точности СИ 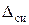 (или
(или  ), то необходимо, чтобы доверительный интервал
), то необходимо, чтобы доверительный интервал  был существенно меньше
был существенно меньше  .
.
Обычно принимают от до
до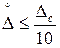 при Р = 0,95.
при Р = 0,95.
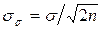 .
.
Принято, что если  , то оценка точности надежна.
, то оценка точности надежна.

Число измерений можно выбрать из данных табл. 2.1 или по одной из формул:

где n от — число отбрасываемых экспериментальных результатов. С учетом коэффициентов Стьюдента можно оценить относительную погрешность отдельного измерения как 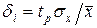 среднего значения
среднего значения 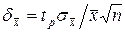 .
.
Таблица 2.1
Необходимое число измерений при нормальном законе распределения случайной величины (при Р = 0,95)
Относительная погрешность, 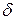
| Коэффициент вариации, 
| |||
| 0,20 | 0,25 | 0,30 | 0,35 | |
| 0,05 | ||||
| 0,10 | ||||
| 0,15 | ||||
| 0,20 | ||||
| 0,25 |
Оставшаяся необнаруженной систематическая составляющая опаснее случайной: если случайная составляющая вызывает вариацию (разброс) результатов, то систематическая — устойчиво их искажает (смещает). В любом случае отсутствие или незначительность (с целью пренебрежения) систематической погрешности нужно доказать.
Действительно, если взять два ряда измерений одной и той же величины, то средние результаты этих рядов, как правило, будут различны. Это расхождение может быть определено случайной или систематической составляющей. Методика выявления характера погрешности заключается в следующем:
1. Из двух рядов  и
и  независимых измерений находят средние арифметические
независимых измерений находят средние арифметические  и
и 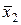 .
.
2. Определяют значения

3. Вычисляют 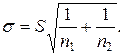
4. Вероятность того, что разность 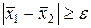 является случайной величиной, определяется равенством
является случайной величиной, определяется равенством  , где
, где  .
.
Величина Р определяется по таблице Стьюдента.
Если полученная вероятность Р > 0,95, то разность 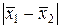 носит систематический характер.
носит систематический характер.
Пример 2.2. Расчетные значения составили tр= 3 и п = 15. По таблице Стьюдента находим, что при п – 1 = 14 и tр = 2,98=3 величина Р = 0,99. Тогда Р = 0,99 > 0,95, что свидетельствует о систематическом характере погрешности.
Субъективные
Методическая
Инструментальная
Профилактика погрешности –
Пример 2.3. Пусть периодическая погрешность меняется по закону
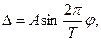
где  независимая величина, от которой зависит
независимая величина, от которой зависит 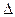 (время, угол поворота и т.д.); Т — период изменения погрешности.
(время, угол поворота и т.д.); Т — период изменения погрешности.
Пусть при 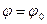 величина
величина 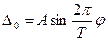 . Находим значение погрешности для
. Находим значение погрешности для  , где
, где 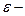 такой интервал, что
такой интервал, что

Определим, чему равен интервал  .
.
Решение. По условию для интервала  имеем
имеем
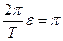 и
и  .
.
В этом случае 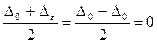 .
.
2.4. Нормирование погрешностей и формы представления результатов измерений.
В соответствии с МИ 1317–86 точность измерения должна выражаться одним из способов:
1)интервалом, в котором с установленной вероятностью находится суммарная погрешность измерения;
2)интервалом, в котором с установленной вероятностью находится систематическая составляющая погрешности измерений;
3)стандартной аппроксимацией функции распределения случайной составляющей погрешности измерения и средним квадратическим отклонением случайной составляющей погрешности измерения;
4)стандартными аппроксимациями функций распределения систематической и случайной составляющих погрешности измерения и их средними квадратическими отклонениями и функциями распределения систематической и случайной составляющих погрешности измерения.
(х = а ± Δ; или Δ от  до
до 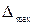 ; Р = 0,90).
; Р = 0,90).
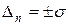 при Р= 0,95 (ГОСТ 8.051– 81).
при Р= 0,95 (ГОСТ 8.051– 81).
2.5. Внесение поправок в результаты измерений.
 .
.
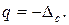 (2.7)
(2.7)

Рис. 2.6. Закон распределения систематической погрешности.


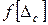
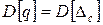 . При
. При 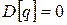
|
|
|
Дата добавления: 2014-01-04; Просмотров: 636; Нарушение авторских прав?; Мы поможем в написании вашей работы!