Магнітне поле у вакуумі

Електричні струми взаємодіють між собою. Взаємодія струмів здійснюється через магнітне поле.

Магнітне поле – це форма матерії, що породжується рухомими зарядами і діє на рухомі заряди.

Магнітна індукція. Для дослідження магнітних полів використовується контур зі струмом малих розмірів (пробний контур). Його орієнтація у просторі визначається позитивною одиничною нормаллю 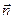, пов’язаною з напрямком струму в контурі правилом правого гвинта (правилом свердлика) (див. рис. 45).

Контур зі струмом характеризується магнітним моментом , який визначається за формулою

,

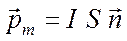де I – сила струму у контурі, S – площа контуру, 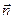– одинична позитивна нормаль.

При внесенні контуру зі струмом у магнітне поле на нього діє обертальний момент , під дією якого контур розвертається й займає рівноважне положення. Відношення максимального обертального момента сил, який діє на контур зі струмом, до магнітного момента контуру, є силовою характеристикою магнітного поля у тому місці, де знаходиться пробний контур, і називається магнітною індукцією .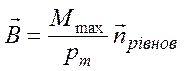

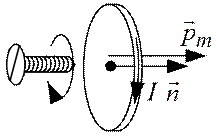
Рис. 45

Напрямок вектора 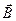визначається рівноважним положенням позитивної нормалі до контуру 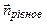. Одиниця вимірювання магнітної індукції в системі СІ 1 Тесла (Тл).

Потік вектора магнітної індукції вводиться аналогічно потоку вектора напруженості електричного поля

,

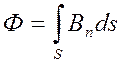де B_n – проекція вектора магнітної індукції 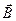на нормаль в кожній точці поверхні інтегрування S. Одиниця вимірювання магнітного потоку в системі СІ – 1 Вебер (Вб)=1 Тл×м².

Для однорідного магнітного поля (вектор 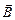у всіх точках поля однаковий за величиною та напрямком) потік вектора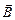через плоску поверхню визначається формулою

Ф = B S cos a = B_n S,

де α – кут між вектором магнітної індукції 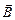і нормаллю до площини, S – площа плоскої площадки.

Потік Ф вектора магнітної індукції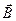визначає кількість ліній магнітної індукції, що перетинають поверхню S.

Лінії магнітної індукції. Магнітні поля зображуються за допомогою ліній магнітної індукції. Потік вектора магнітної індукції через замкнену поверхню S дорівнює нулю

.

Звідси випливає, що лінії магнітної індукції – замкнені криві. У просторі їх проводять так, що в кожній точці вектор 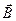направлений вдовж дотичної до лінії магнітної індукції, а густина ліній дорівнює самій індукції (див. рис. 46).

Рис. 46

Для магнітного поля, як і для електричного, виконується принцип суперпозиції

,

тобто індукція системи струмів дорівнює векторній сумі індукцій магнітних полів, утворених кожним із струмів окремо.

Закон Біо-Савара-Лапласа. Він визначає магнітну індукцію елемента струму , тобто малої ділянки провідника зі струмом довжини dl, напрямок якої збігається з напрямком струму. Індукція елемента струму визначається за формулою

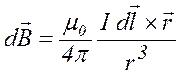, (4.15)

де – радіус-вектор, який проведено з елемента струму 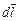у точку спостереження, хрестик означає векторний добуток, m₀= 4p×10^-7 Гн/м – магнітна стала (див. рис. 47).

Рис. 47

У скалярній формі формулу (4.15) записують так:

,

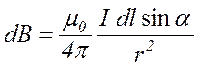де α – кут між векторами 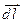і .

Поле прямого струму. Розбиваючи провідник на елементи струму і використовуючи закон Біо-Савара-Лапласа і принцип суперпозиції, можна визначити магнітну індукцію будь-якого провідника зі струмом. Для прямого нескінченно довгого провідника зі струмом в результаті отримаємо формулу для індукції

, (4.16)

де r – відстань від струму до точки спостереження. Лінії магнітної індукції прямого провідника зі струмом являють собою концентричні кола (див. рис. 48).

Для обмеженого за довжиною прямолінійного провідника зі струмом індукція визначається формулою

, (4.17)

де α₁ і α₂ – кути між провідником і радіус-векторами, відповідно, і 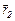, що проведенні із точок спостереження у кінці провідників (див. рис. 49).

Рис. 48

Рис. 49

При α₁ ®0 і α₂®0 (тобто при переході до необмеженого провідника) формула (4.17) переходить у формулу (4.16) для нескінченно довгого провідника.

Циркуляція вектора магнітної індукції – це інтеграл по замкненому контуру L: 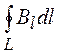, де В_l – проекція вектора 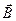на елементарну ділянку інтегрування 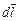, тобто на напрямок дотичної в кожній точці контуру (див. рис. 50).

Якщо контур інтегрування L охоплює кілька струмів, то циркуляція вектора магнітної індукції 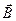дорівнює добутку магнітної сталої m₀ на суму струмів, що охоплюються контуром інтегрування:

. (4.18)

Позитивними у формулі (4.18) вважаються струми, напрямок яких пов’язаний з напрямком інтегрування правилом правого гвинта (правило свердлика). Формула (4.18) має назву закону повного струму.

Поле соленоїда. Використовуючи формулу (4.18) для циркуляції вектора магнітної індукції 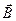, легко отримати формулу для індукції магнітного поля нескінченно довгого соленоїда.

В=m₀ n I (всередині соленоїда), (4.19)

B=0 (зовні соленоїда),

Рис. 50

Рис. 51

де n – кількість витків, що припадають на одиницю довжини соленоїда. Таким чином, магнітне поле нескінченно довгого соленоїда однорідне і повністю зосереджене всередині соленоїда.(див. рис. 52).

Для обмеженого соленоїда лінії індукції магнітного поля замикаються через вільний простір (див. рис. 53). Всередині достатньо довгого соленоїда (довжина якого набагато більша його діаметра) магнітне поле практично однорідне і добре описується формулою (4.19). Однорідність поля порушується тільки поблизу кінців соленоїда.

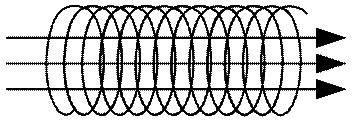Рис. 52

Рис. 53

Дата добавления: 2014-01-04