Дифракція світла

Огинання хвилями перешкод називається дифракцією. Виникнення дифракції можна пояснити за допомогою принципу Гюйгенса: кожна точка хвильового фронту є джерелом вторинних сферичних хвиль, огинаюча яких дає положення хвильового фронту в наступний момент часу (див. рис. 73, а).

Промені світла поширюються вздовж нормалі до хвильового фронту. Тому дифракція світла призводить до проникнення світла в область геометричної тіні і утворення дифракційної картини – світлих і темних ділянок, які чергуються (див. рис. 73, б, в).

Дифракція дуже залежить від співвідношення розмірів перешкоди d на шляху світла і довжини хвилі l. Дифракція найбільш яскраво виражена при d»l.

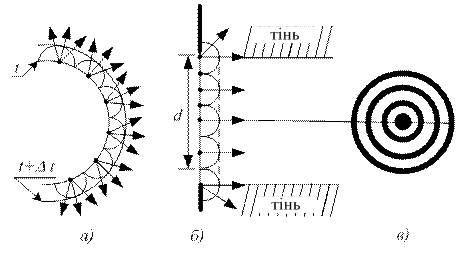
Рис. 73

Принцип Гюйгенса-Френеля. Принцип Гюйгенса дозволяє тільки якісно пояснити явище дифракції, але не дозволяє визначити амплітуди розсіяних перешкодою хвиль, які поширюються в різних напрямках. Френель доповнив принцип Гюйгенса уявленням про інтерференцію вторинних хвиль. Врахування амплітуд і фаз вторинних хвиль дозволяє знайти амплітуду розсіяної перешкодою світлової хвилі в будь-якій точці простору.

Результуюче коливання в будь-якій точці спостереження P являє собою суперпозицію коливань, що проходять від усіх елементів хвильової поверхні S з урахуванням їх амплітуд і фаз:

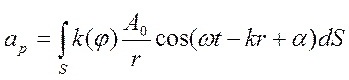, (6.9)

де 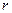– відстань від елемента dS хвильової поверхні 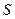до точки спостереження 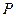(див. рис. 74), – амплітуда коливань на елементі dS, w=2p /Т – циклічна частота коливань, k=2p/l – хвильове число. Отже результуюче коливання в точці Р дорівнює сумі (тобто інтегралу) коливань, що приходять в точку 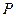від всіх елементів хвильової поверхні S з уврахуванням їх амплітуд і фаз. Це і є принцип Гюйгенса-Френеля.

Рис. 74

Види дифракції:

1) дифракція Фраунгофера, або дифракція в паралельних променях, коли відстані від джерела світла S до перешкоди, на якій відбувається дифракція, і відстань від перешкоди до точки спостереження P великі порівняно з розмірами перешкоди. При цьому промені, що падають від джерела світлу на перешкоду,

і промені, що поширюються від перешкоди в точку спостереження, йдуть практично паралельними пучками (див. рис. 75, а);

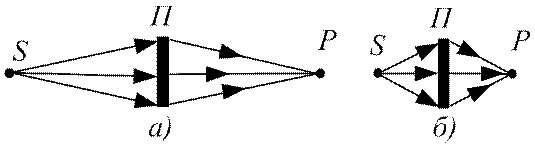
Рис. 75

2) дифракція Френеля – це дифракція в непаралельних променях, коли джерело світла і точка спостереження лежать недалеко від перешкоди (див. рис. 75, б)

Зони Френеля. Принципом Гюйгенса-Френеля (6.9) важко скористатися на практиці, оскільки важко підрахувати інтеграл по хвильовій поверхні S. Для полегшення цього Френель запропонував розбити поверхню інтегрування S (а це хвильова поверхня) на окремі ділянки, різниця ходу променів від меж яких дорівнює . Ці ділянки хвильової поверхні отримали назву зон Френеля. Тоді результуючі коливання, що утворюються в точці спостереження Р вторинними хвилями від двох сусідніх зон Френеля, находяться у протифазі, тобто відрізняються за фазою на p. Тому амплітуда результуючого коливання, що утворюється в точці спостереження Р вторинними хвилями, які прийшли від всієї хвильової поверхні, визначається формулою.

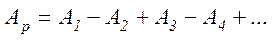, (6.10)

де А_m – амплітуда, утворена вторинними хвилями, які прийшли від m -ї зони Френеля.

Для точкового джерела світла хвильова поверхня сферична і зони Френеля для неї являють собою кільцеві області (крім першої) з радіусом зовнішньої межі

,

де 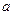– радіус сферичної хвильової поверхні (див. рис. 76) 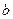– відстань від вершини сферичного сегменту (точка О) до точки спостереження Р (вимірюється уздовж лінії, яка з’єднує джерело S і точку спостереження Р).

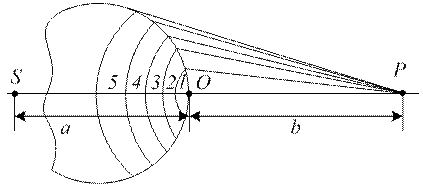
Рис. 76

Формулу (6.10) можна переписати у вигляді

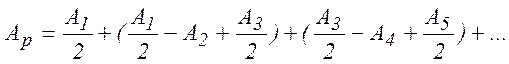
Для сферичної хвильової поверхні амплітуди А_m утворюють послідовність, що монотонно зменшується. Тому і в результаті

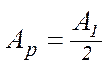, (6.11)

Тобто амплітуда, що утворюється в точці Р сферичною хвильовою поверхнею, дорівнює половині амплітуди, що утворюється однією центральною зоною.

Дифракція Френеля на круглому отворі. При дифракції сферичної хвилі на круглому отворі радіусу r₀ відкритими є зон Френзеля, де а – відстань від джерела світла до отвору, b – відстань від отвору до точки спостереження. Джерело S і точка спостереження Р лежать на осі симетрії отвору. Амплітуда коливань в точці Р

,

де знак плюс береться, якщо кількість зон Френеля, що відкриває отвір, непарне, а знак мінус, якщо число зон парне. За малої кількості відкритих зон Френеля А₁»А_m і

За відсутності перешкоди A_p=A₁ /2 відповідно до формули (6.11). Таким чином, перешкода з отвором, який відкриває непарну кількість зон Френзеля, не тільки не послаблює світло, а навпаки, призводить до збільшення амплітуди коливань в точці Р у два рази, а інтенсивності коливань – у 4 рази. Це суттєво хвильовий ефект, який у межах геометричної оптики пояснити неможна.

При переміщенні точки спостереження у площині, паралельній площині з отвором, спостерігається дифракційна картина у вигляді світлих і темних кілець з максимумом у центрі, якщо отвір відкриває непарну кількість зон Френеля (див. рис. 77, а), і з мінімумом, якщо m – парне (див. рис. 77, б).

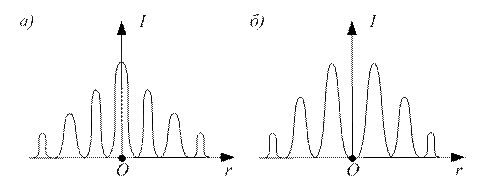
Рис. 77

На рис. 77 показані профілі інтенсивності світла залежно від відстані r від осі отвору. Якщо отвір відкриває не більше однієї зони Френеля, то на екрані розмита світла пляма.

Дифракція Фраунгофера на щілині. При дифракції паралельного пучка променів на щілині в екрані, промені розсіюються по всіх напрямках. Промені, які йдуть в одному напрямку, інтерферують між собою і в результаті на екрані спостерігається дифракційна картина. При нормальному падінні променів на щілину шириною b, різниця ходу крайніх променів, що йдуть під кутом дифракції j (цей кут відраховується від нормалі до площини щілини), дорівнює bsinj (див. рис. 78, а).

Рис. 78

Якщо виконується умова

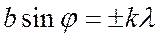, k=1,2,3,…, (6.12)

то хвильова поверхня на щілині розбивається на 2k (парну) кількість зон Френеля. Дії зон попарно компенсують одна одну і під даним кутом дифракції спостерігається дифракційний мінімум.

Якщо виконується умова

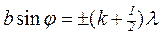, k=1,2,3,…,

то на отворі вкладається 2k+1 (непарна) кількість зон Френеля. Дія однієї зони залишається незкомпенсованою і під даним кутом дифракції спостерігається дифракційний максимум.

Дифракційна картина являє собою чергування світлих і темних смуг. На рис. 78, б показано залежність інтенсивності дифрагованого світла від кута дифракції j. Під кутом j =0 всі вторинні промені накладаються в однаковій фазі і під цим кутом дифракції спостерігається головний дифракційний максимум (k=0). Світлі смуги дифракційної картини відповідають максимумам інтенсивності, а темні – мінімумам.

Дифракційні ґратки. Періодична послідовність щілин у екрані утворює дифракційну ґратку. Коливання, що поширюються від різних щілин ґратки, є когерентними і інтерферують. Результат накладання (підсумовування) коливань залежить від різниці фаз коливань для двох сусідніх щілин , де 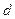– період дифракційної ґратки, 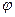– кут дифракції (див. рис. 79).

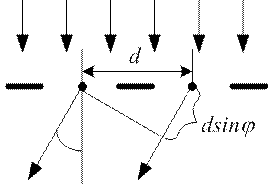
Рис. 79

За умови

, (6.13)

де m=0,1,2… – максимуми від окремих щілин накладаються в однаковій фазі і підсилюють один одного. Під такими кутами дифракції j спостерігаються головні дифракційні максимуми для ґратки. Формула (6.13) має назву формули дифракційної ґратки.

Умова (6.12) для дифракційних мінімумів для окремих щілин є одночасно і умовою для дифракційних мінімумів всієї ґратки.

Дифракційну картину при дифракції на ґратці пучка монохроматичного світла показано на рис. 80, а.

Рис. 80

Максимальний порядок (m) головних максимумів знаходиться з умови

.

Оскільки кут дифракції не може перевищувати 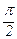, то кількість максимумів дорівнює 2m+1.

Положення головних максимумів залежить від довжини хвилі 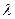. Тому при падінні на дифракційну ґратку білого світла всі максимуми дифракційної картини, крім центрального 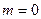, розкладаються у спектр (див. рис. 80, б). Амплітуда в головному максимумі дифракційної ґратки , де – амплітуда у максимумі для окремої щілини, 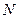– кількість щілин дифракційної ґратки. Тоді інтенсивність головних максимумів дифракційної ґратки 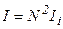. Тому максимуми дифракційної картини для ґратки дуже насичені і дифракційна ґратка вважається кращим спектральним приладом (тобто приладом для розкладання випромінювання у спектр).

Дата добавления: 2014-01-04