Рівняння Нав'є-Стокса

Виділимо в потоці рідини, що рухається по каналу, елементарний паралелепіпед з ребрами dx,dy,dz (рис.3.2.1). На цей елемент діють три сили: сила тяжіння, сила тиску і сила тертя.

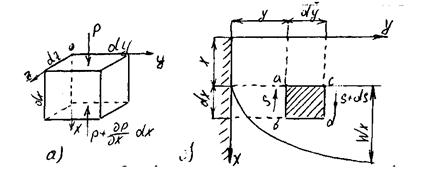
Рис. 3.2.1. До виведення диференційного рівняння руху в'язкої рідини,що не стискується

. Сила тяжіння може бути визначена з виразу:

G=g×r×dx×dy×dz

де р- густина рідини;

g- прискорення вільного падіння.

V=dx×dy×dz,

де V-об¢єм паралелепіпеда.

Силу тиску можна знайти з наступних міркувань. Гідростатичний тиск в даному випадку змінюється вздовж вертикальної вісі. Нехай на верхній грані значення тиску р, тоді на верхню грань діє сила:

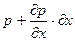P=p×dy×dz (Рис.2.1.2..б). Тиск біля нижньої грані елемента рівний:

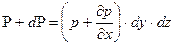тому сила тиску рівна:

Результуюча цих сил і буде силою тиску, що діє на елемент:

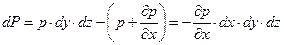
(3.2.1)

Силу тертя виразимо виходячи з припущень про плоско-паралельний рух потоку. В цьому випадку локальні швидкості руху частинки в потоці W_X (рис. 3.2.1 б) змінюються лише в напрямку вісі у, а тертя виникає лише на бічних гранях AB і CD. Біля грані AB швидкість руху рідини менше, ніж швидкість руху виділеного елементу, тому сила тертя напрямлена проти руху. Якщо силу тертя, віднесену до одиниці поверхні, позначити через s¢, то сила тертя, що діє на грань AB, буде S=s¢×dx×dz.

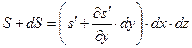(3.2.2)

Біля грані CD швидкість руху частинок більша, за швидкість руху елемента, і силу тертя, напрям котрої співпадає з напрямом руху елемента, можна виразити як

Результуюча зазначених сил і є сила тертя, що діє на елемент потоку рідини:

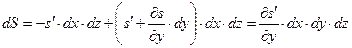(3.2.3)

Згідно закону Ньютона-Петрова:

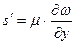
Тому силу тертя можна виразити як:

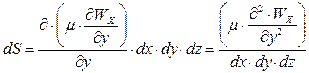(3.2.4)

На основі другого закону механіки (рівнодіюча сила дорівнює масі, помноженій на прискорення) для даного випадку запишемо:

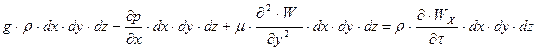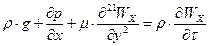(3.2.5)

це диференційне рівняння для рівномірного сталого руху незріджуючої в'язкої рідини.,що не стискується.

Для випадку трьохмірного несталого руху в'язкої рідини (r=const),що не стискується отримують більш складні рівняння, але структура їх зберігається:

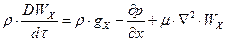
(3.2.6)

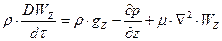
Рівняння (2.1.6) руху в’язкої рідини, що не стискується називають рівняннями Нав"є-Стокса. Де похідні DW_X/dt, DW_Y/dt, DW_Z/dt в лівій частині рівняння (3.2.6) являють собою повні похідні швидкості по часу:

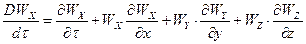
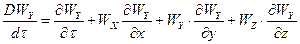(3.2.7)

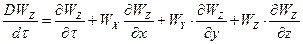
Перші члени доданків правих частин рівнянь (3.2.7) визначають локальні зміни складових швидкості у часі. Три останні доданки правих частин рівнянь враховують переміщення елементу рідини з однієї точки простору в іншу.

Величини g_Х, g_У, g_Z - складові рівняння вільного падіння в напрямку окремих вісів координат.

Символом V² (набла) позначений оператор Лапласа, що є сума других похідних:

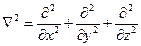(3.2.8)

Дата добавления: 2014-01-04