Вибірковий метод.

План.

1. Поняття і суть вибіркового методу, причини і умови його застосування.

2. Види і способи вибіркового спостереження.

3. Визначення середньої і граничної помилки.

4. Визначення обсягу вибірки.

5. Особливості малої вибірки

v Вибірковим називається таке спостереження, яке дає характеристику всієї сукупності одиниць на основі дослідження її частини.

Не завжди можна використовувати суцільне спостереження і тоді використовують вибіркове спостереження. Крім того воно використовується для уточнення результату суцільного спостереження (наприклад, при переписі 1979 року поруч із суцільним спостереженням певну групу людей досліджували спеціально за більш розширеними анкетами). Крім того вибіркове спостереження використовується при експериментах в природничих науках. Має воно використання і в таких економічних галузях дослідження, як митне обстеження якості продукції.

Основні завдання вибіркового спостереження такі:

1) вивчення середнього розміру досліджуваної ознаки;

2) вивчення питомої ваги (частки) досліджуваної ознаки в сукупності.

Основні поняття вибіркового методу такі.

Розрізняють генеральну сукупність і вибіркову сукупність. Генеральна сукупність – це загальна сукупність одиниць, з якої проводиться відбір. А вибірковою називається частина генеральної сукупності, яка підлягає обстеженню.

Обсяг генеральної сукупності позначають через літеру N. Обсяг вибіркової сукупності – n. Відповідно генеральна середня позначається: 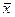, а середня вибіркова - 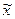. Звісно, що генеральна і вибіркова середні не співпадають. Це пов'язано з помилкою репрезентативності.

Гранична помилка репрезентативності 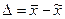, або , де w – частка досліджуваної ознаки в генеральній сукупності, а p – частка досліджуваної ознаки в вибірковій сукупності).

Точність результатів вибіркового методу залежить від

- способу відбору одиниць,

- ступеня коливання ознаки у сукупності,

- числа одиниць, що спостерігаються.

За способами відбору одиниць розрізняють такі види вибіркового спостереження:

1) власне випадкова вибірка – така вибірка, при якій відбір одиниць з усієї генеральної сукупності є ненавмисним (випадковим). Для цієї вибірки характерне жеребкування.

Розрізняють повторну і безповторну випадкову вибірку. При повторній виборці кожна одиниця може бути вибрана декілька разів, а при безповторній кожна одиниця сукупності обирається лише один раз. Найчастіше застосовується повторна випадкова вибірка.

2) механічна вибірка – це така вибірка, при якій відбір одиниць проводиться механічно через певний інтервал. Механічна вибірка завжди безповторна.

Недоліком механічної вибірки є те, що перед вибіркою необхідно мати повий облік одиниць сукупності, потім потрібно провести ранжування і лише після цього можна проводити вибірку з певним інтервалом.

3) типова (районована) вибірка – це така вибірка, при якій генеральну сукупність поділяють на однорідні групи за певною ознакою (або на райони і зони). Потім з кожної групи у випадковому порядку відбирається певна кількість одиниць, пропорційно питомій вазі групи в загальній сукупності.

Типова вибірка часто здійснюється в декілька ступенів.

4) серійна вибірка – це така вибірка, при якій відбір одиниць проводиться групами (серіями) і обстеженню підлягають усі одиниці відібраної групи (серії).

Перевагою серійної вибірки є те, що інколи відібрати окремі одиниці складніше, ніж серії. Прикладом є 10% відбори певної серії випуску продукції (напр. зернових).

5) В статистичній практиці часто застосовується не один, а декілька видів вибірки. Таке спостереження називається комбінаційним.

Помилки репрезентативності можуть бути систематичні і випадкові. Систематичні помилки виникають внаслідок порушення принципів проведення вибіркового спостереження. Випадкові помилки репрезентативності зумовлені тим, що вибіркова сукупність не відображає точно середні і відносні показники генеральної сукупності.

Фактори, що впливають на помилки репрезентативності:

- показники варіації певної ознаки (напр. дисперсії): чим більший показник варіації – тим більше розмір помилки

- від чисельності вибірки: чим більша вибірка – тим менша вірогідність помилки (розмір помилки).

- від способу відбору (повторний чи безповторний).

Середня помилка репрезентативності (інша назва – стандарт). Позначається (мю).

Формули для обрахування середньої помилки репрезентативності для механічної і випадкової вибірки (див. таблицю)

	Спосіб відбору
Повторний	Безповторний
При визначенні середньої розміру досліджуваної ознаки (x)
При визначенні частки досліджуваної ознаки (w)

n – кількість одиниць вибіркової сукупності

N – кількість одиниць генеральної сукупності

- частка одиниць сукупності, що досліджуються

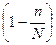- частка одиниць сукупності, що не досліджуються.

Задача. При проведення 5% механічної вибірки дістали дані про врожайність нового сорту пшениці:

Урожайність, ц/га	20-22	22-24	24-26	26-28	28-30	Всього
Посівна площа, га

Визначити середню помилку репрезентативності:

1) при встановленні середньої очікуваної врожайності нового сорту пшениці;

2) при визначенні питомої ваги посівної площі нового сорту пшениці урожайність якої перевищує 26 ц/га.

Рішення.

1) Для нашої вибірки середня врожайністьц/га, дисперсія .

За умовою. Оскільки маємо 5% вибірку, то

Тоді

Отже, 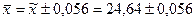Þ

2) Питома вага посівної площі з врожайністю більше 26 ц/га:

Тоді середня помилка репрезентативності становить:

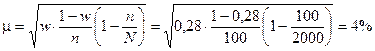
Отже питома вага посівної площі, на якій врожайність перевищуватиме 26 ц/га, становить 28% ± 4%.

Для вирішення практичних завдань обчислення середньої помилки вибірки недостатньо, тому визначають граничний для певної імовірності розмір вибіркової помилки Δ = t • μ, де t — квантиль нормального розподілу, який називають коефіцієнтом довіри.

Розглянемо приклади визначення граничної помилки середньої та частки.

Приклад 1

З отари овець загальною чисельністю 1000 голів (N) вибірковій контрольній стрижці було піддано 100 голів (п), середній настриг вовни при цьому становив 4,2 кг на одну вівцю при cередньому квадратичному відхиленні 1,5 кг. Визначити межі, в яких знаходиться середній настриг вовни для усіх 1000 голів з імовірністю 0,954 (t= 2).

У даному разі маємо простий випадковий відбір, до того ж, зрозуміло, безповторний.

Підставимо дані у відповідні формули:

Δ= 2·0,142= 0,284кг.

Тоді одне із можливих значень, в межах яких може знаходитись середній настриг вовни, розраховуєтся за формулою

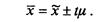
У загальному вигляді це записується таким чином:

х = 4,2 ± 0,284, що дорівнює:

3,92 ≤ x ≤ 4,48.

Таким чином, на підставі проведеної вибірки гарантуємо, що у 954 випадках із 1000 середній настриг вовни буде знаходитися в межах: від 3,9 до 4,4 кг на одну вівцю.

Приклад 2

Для визначення якості продукції відібрано 500 одиниць з 10 000. Серед них виявлено 50 виробів тре­тього сорту. Визначити граничну помилку частки з імовірністю 0,997.

Маємо, що частка виробів третього сорту становить

W=50/500=0,1,

тоді частка першого та другого сортів становить

р= 1 - W = 1 -0,1 =0,9.

Підставимо дані в формулу для простого випадко­вого безповторного відбору:

μ=

p=0,9 ±3•0,0131.

Таким чином, на підставі проведеної вибірки встановлено, що середній відсоток виробів третього сорту становить 10 % з можливим відхиленням в той чи інший бік на 3,9 %. З імовірністю 0,997 можна стверджувати, що середній відсоток виробів третього сорту в усій партії буде знаходитись у межах

р = 10% ± 3,9%, тобто 6,1% - 13,9%.

Наведені вище формули середньої та граничної помилки вибірки застосовують при випадковому та механічному відборах.

При типовому відборі гранична помилка визначається за такими формулами (табл. 4.1).

Таблиця 4.1 Граничні помилки вибірки при типовому відборі

Схема вибору	Гранична помилка вибірки
Для середньої	Для частки
Повторний	∆x=t	∆x=t√w(1-w)/n
Безповторний	∆x=t√σ^2b/n(1-n/N)	∆w=t√w(1-w)/n(1-n/N)

Якщо порівняти їх з формулами для випадкового відбору, то виявиться, що замість дисперсії і частки, що визначаються для вибіркової сукупності в цілому, при типовому відборі необхідно обчислити середні з

групових дисперсій і частки, що отримані для кожної групи:

Приклад 4.3

Проведена 10-процентна типова вибірка, пропор­ційна чисельності відібраних груп робітників (табл. 4.2).

Визначити з імовірністю 0,954 межі, в яких знахо­диться середній відсоток виконання норм робітниками в цілому. Вибірка безповторна.

Таблиця 4.2 Характеристика вибірки робітників

Групи робітників за спеціальністю	Чисельність, чол.	Середнє виконання норми, %	Середнє квадратичне відхилення, %
т
с
ф

Обчислимо загальний середній відсоток виконання норми робітниками, які потрапили у вибірку:

x=98·4+108·50+104·60/150=103,7%

Визначимо середню із групових дисперсій:

σ²_b=4·40+9·50+25·60/150=14,%1

Гранична помилка вибіркової середньої для ти­пового відбору:

∆_x=2∙√14,1/150(1-150/1500)=0,581%

де N= І 500, так як вибірка 10-процентна.

Таким чином, з імовірністю 0,954 можна стверджу­вати, що середній відсоток виконання норм робіт­никами заводу в цілому знаходиться в межах

х = 103,7 ± 0,581,

звідси

103,1 ≤ х ≤104,3.

При серійному відборі з рівновеликими серіями гранична помилка визначається за формулами наведеними в табл. 4.3, де S — загальне число серій у сукупності. У даному випадку кожна серія являється одиницею сукупності, і мірою коливання буде міжсерійна вибіркова дисперсія:

δ²=Σ(x_i-x)²/s

де x_i, — середня для кожної серії; х — загальна вибіркова середня, з — число відібраних серій.

Таблиця 4.3 Граничні помилки вибірки при серійному відборі

Якщо порівняти їх із формулами для випадкового відбору, то виявиться, що замість дисперсії і частки, які визначаються для вибіркової сукупності в цілому, при серійному відборі необхідно обчислити міжгру-пову дисперсію середньої і частки.

Приклад 4.4

Для визначення середньої врожайності цукрового буряка в області проведена 20-процентна серійна вибірка, до якої відійшло 5 районів із 25. Середня врожайність для кожного району становила: 250, 260, 275, 280, 300 ц/га з площі 800, 1000, 1200, 1200 і 2800 га відповідно. Визначити з ймовірністю 0,954 межі, в яких буде знаходитись середня врожайність цукрового буряка по області.

Спочатку знайдемо загальну середню:

x= 250-800+260-1000+275-1200+280-1200+300-2800^ =

800+1000+1200+1200+2800

=280 ц/га.

Визначимо міжсерійну дисперсію:

= _ (250 - 28О)² + (260 - 280)²1000 + (270 - 280)²1200+

800+1000+1200+1200+2800

+(280-280)²1200+(300-280)²2800 800+1000+1200+1200+2800

Розрахуєм граничну помилку серійного безповторного вибору:

Отже, з ймовірністю 0,954 можна стверджувати, що середня врожайність цукрового буряка по області буде знаходитись в межах від 272,66 ц/га до 287,34 ц/га. Таким чином розраховуються середня і гранична по­милки для частки.

4. Перед тим, як приступити до проведення вибіркового спостереження, треба визначити необхідну чисельність вибірки, тобто такий обсяг вибіркової сукупності, який забезпечив би необхідну точність результатів.

Необхідна чисельність п визначається на основі формул граничної помилки. Формули для випадкового та механічного відборів наведені в табл. 4.4.

Таблиця 4.4 Визначення обсягу вибіркової сукупності

Схема відбору	Обсяг вибірки
При визначенні середньої	При визначенні частки
Повторний	nx=t ^2σ x^2/Δ^2x	nw =t^2w(1-w)/Δ w^2
Безповторний	nx = Nt ^2σ x^2/NΔ^2x + +t ^2σ x^2	nw =Nt^2w(1-w)/NΔ^2w +t^2w(1-w)

Приклад 4.5

У районі є 2 500 корів. Треба визначити необхідний обсяг випадкової вибірки для повторної та безповторної схеми при умові, що гранична помилка обчис­лення середнього річного надою не буде перевищувати

20 кг при імовірності 0,954 та сг, = 300. Для повторного відбору

n_x =4•300²/ 20² =900 голів

Для безповторного відбору

n=2500•4•300²/2500•4+4•300²=662 голови

Приклад 4. 6

Визначимо обсяг вибірки при обчисленні частки. Встановлено, що помилка частки з імовірністю 0,954 не повинна перевищувати 3 % при питомій вазі поро­дистих корів у 80 %.

Для повторного відбору

n_w=4•0,16.0,03 =711 корів.

Для безповторного відбору:

n_w = 2500•4•0,16/2500•0,03²+4•0,16 = 554 корови.

При визначенні необхідного обсягу вибірки σ _x² і р(W) генеральної та вибіркової сукупності невідомі. Тому ці значення встановлюють приблизно на підставі аналогічних або пробних досліджень. Якщо ознака альтернативна, то вважають, що W= 0,5, W(1 —W) = 0,25.

5. Малою вибіркою прийнято вважати вибірку, об'єм якої варіює в межах від 5 до ЗО одиниць. Мала вибірка являється єдиним методом дослідження в тих випадках, коли організація суцільного або великого вибіркового спостережень неможлива. Переважно ви­бірковим методом користуються у випадку дослід­ження якості промислової продукції, при встановленні норм виробітку. Однак, слід відмітити, що необхідно бути обережним при використанні малої вибірки.

Як відомо з теорії вибіркового спостереження, репрезентативність вибірки в значній мірі залежить від її обсягу. Випадкові помилки вибірки при достатньо великому обсязі розподіляються нормально. При цьому допускається умова рівності генеральної та вибіркової дисперсії.

За умови малої вибірки цим припущенням користуватись не можна. Її особливість якраз і полягає в тому, що випадкові помилки малої вибірки не підчиняються закону нормального розподілу. Тому для оцінки результатів малої вибірки і можливих границь її випадкової помилки користуються відношенням Стьюдента:

де ^ — стандартна помилка малої вибірки, яка обчис­люється за формулою

Як бачимо з цієї формули, в знаменнику береться не п, як у звичайній-вибірці, а п — 1, що являється принципово важливим у випадку для розрахунку помилки малої вибірки. Гранична ж помилка малої вибірки обчислюється стандартним способом за

формулою

Δ=t·μ_m

де t — це відношення Стьюдента.

Величина t підпорядковується закону розподілу Стьюдента (t вірне тільки для виборок, які взяті із генеральної сукупності з нормальним розподілом ознак). Для визначення ймовірності інтенсивності Р(t) користуються спеціальними таблицями, в яких роз­раховані Р(t) для даних значень t і k = п — 1 (k — число ступенів вільності).

Наведемо приклад у вигляді табл. 4.5.

Таблиця 4.5 Імовірність Р(t) розподілу t (Р_k(і) • 1000)

T	К
								∞
2.0
2.5
3.0

За цією таблицею визначається двосторонній критерій, тобто імовірність того, що фактичне значення і через випадкові причини не буде більшим від табличного за абсолютною величиною.

Приклад 4.7 [9]

На електроламповому заводі з метою перевірки якості ламп була організована мала вибірка (табл. 4.6). У випадковому безповторному відборі було відібрано 10 ламп.

Необхідно визначити граничну помилку вибірки і побудувати довірчий інтервал для середньої.

Таблиця 4.6 Розрахунок граничної помилки вибірки

Тривалість горіння, год. (X,)	Число ламп, шт.(fi)	xi ∙fi	xi -x	(xi –x)^2	(xi –x)^2fi
				676
Разом			X	X

Вибіркова середня дорівнює

вибіркова дисперсія:

стандартна помилка:

В умовах малої вибірки при k = п— 1 = 9 і t = 2,5 з імовірністю Рk(t), що дорівнює 0,966, гранична помилка за абсолютною величиною не перевищить

∆_m=2,5•6=15 год.

Імовірність того, що це твердження невірне і по­милка може вийти за встановлені межі 15 год., дорівнює: 1 - 0,966 = 0,034.

На основі розрахованих характеристик будуємо довірчий інтервал для генеральної середньої:

1491 ≤ х ≤ 1521.

Дата добавления: 2014-01-04