Визначення напружень у масивах грунту. деформації у масивах грунту

1) Основні положення про розподіл напружень і деформацій у точці масиву грунту.

Схема розподілу напружень в елементарному об’ємі грунту. Напруження, деформації та переміщення в них.

Тиск від навантаження, прикладеного до грунтового масиву, наприклад, через підошву фундаменту чи бічну поверхню вістря палі, передається в грунті частинками або структурними агрегатами через точки контакту, розподіляючись за глибиною на все більшу площу. Напруження при цьому зменшуються. Відбувається процес розсіювання або затухання напружень за глибиною й з віддаленням в сторони. Напруження в окремих частинках і міжчастинкових зв'язках у межах якого-небудь виділеного перерізу, зокрема АВ на рис. 6.4, а, можуть бути більшими, ніж їх міцність, і спричиняти руйнування. При розгляді напруженого стану масиву грунту подібну місцеву концентрацію напруження, на яку може суттєво впливати просторове розташування окремих часток і зв'язків між ними, умовно не враховують (окрім моделей дискретного середовища). Вважають, що вона не впливає на стійкість масиву в цілому.

Для обгрунтування цього введено поняття елементарного об'ему грунту, тобто такого його об'єму, лінійний розмір якого в багато разів перевищує лінійний розмір частинок або агрегатів, котрі складають цей грунт. Тоді, на відміну від суцільного середовища, для оцінювання напружень у грунтах, що є дисперсними системами, реальні сили, які діють на окремі грунтові частинки, замінюють уявними силами, розподіленими по всьому елементарному об'єму, в тому числі й у проміжках між частинками. Значення цих сил, віднесених до одиниці площі перерізу цього об'єму умовно приймають за значення напружень у грунті (див., наприклад, лінію 2 на рис. 6.4, а).

а)

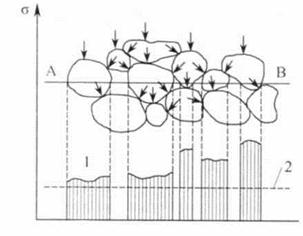
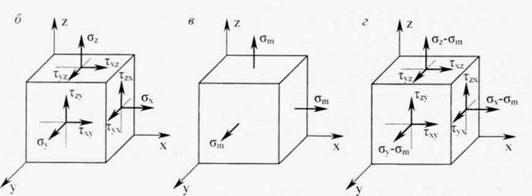
Рис.6.4 Схема розподілу напружень: а - між частинками ґрунту; б - в елементарному об'ємі ґрунту; в-у вигляді шарового тензора та г - девіатора напружень; 1 - фактичні напруження у частинках грунту; 2 - середня величина напружень у грунті.

Крім того, розміри зразка грунту для експериментальних визначень характеристик його механічних властивостей у припущенні суцільності матеріалу повинні бути значно більше від лінійного розміру елементарного об'єму грунту. Використання апарату механіки суцільного середовища для розрахунків напружень і деформацій у масиві фунту виявляється справедливим лише у випадках, коли розміри масиву та розміри ділянок, через які передаються навантаження на масив, значно більше від розміру елементарного об'єму ґрунту.

Мірою кількісної оцінки напружено-деформованого стану (НДС) масиву ґрунтів є напруження, деформації та переміщення, що виникають у ньому від дії зовнішніх (навантаження від споруд) і внутрішніх (власна вага ґрунтів) сил. Ці поняття відповідають загальним визначенням механіки суцільного середовища.

У системі прямокутних координат напружений стан елементарного об'єму грунту можна охарактеризувати сукупністю діючих у ньому напружень (рис. 6.4, б): σ_z- вертикальне нормальне напруження, що діє у напрямі осі z; σ_у ^_ горизонтальна нормальне напруження, що діє у напрямі осі у; σ_х – горизонтальне нормальне напруження, що діє у напрямі осі х; τ_xy τ_yx — дотичні напруження, що діють по гранях, паралельних осі z, однакові між собою відповідно до правила "парності напружень" (τ_ху=τ_ух); τ_zx, τ_xz - однакові між собою дотичні напруження, що діють по гранях, паралельних осі у (τ_zx=τ_xz); τ_yz, τ_zy - однакові між собою дотичні напруження, що діють по гранях, паралельних осі х (τ_yz=τ_zy). Оскільки ґрунти, як правило, дуже погано працюють на розтягання, в механіці ґрунтів на відміну від механіки суцільного середовища стискаючі напруження приймають зі знаком "плюс", а розтягаючі - зі знаком "мінус".

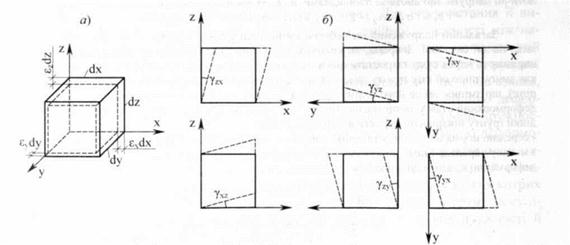
Рис. 6.5. Компоненти деформацій: а- лінійні деформації; б- кутові деформації.

Деформований стан елементарного об'єму грунту визначають компоненти: три лінійні деформації (характеризують відносні подовження ребер елементарного паралелепіпеда) ε_х, ε_у-, ε_z (рис. 6.5.a), три пари взаємно рівних кутових деформацій (відносних зрушень - характеризують зміни кутів між гранями паралелепіпеда) ν_xy=ν_yx, ν_yz=ν_zy,ν_zx=ν_xz (рис. 6.5, б) та переміщеннями – u, v, w.

Дев'ять величин, шо характеризують напружений стан елементарного об'єму грунту, утворюють так званий тензор напружень і називаються його компонентами:

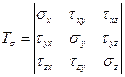
За аналогією тензор деформацій:

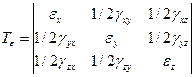
Величини тензорів напружень і деформацій співвіднесені із системою координат х, у, z і при зміні її теж змінюються. Однак напружений стан у точці масиву як фізичний об'єкт, звичайно, не може залежати від довільної системи координат, і тому повинен мати характеристики, не залежні від неї. тобто інваріантні по відношенню до системи координат. До інваріантних характеристик напруженого стану належать, зокрема, головні площадки й головні напруження yz, які можна вказати для будь-якого тензора напружень. Три головні взаємно перпендикулярні площадки характерні тим. шо за ними діють лише нормальні напруження, а дотичні відсутні. При цьому завжди приймають, шо σ₁>σ₂>σ₃. Знаючи головні нормальні напруження, можна визначити й головні дотичні напруження, що діють за площадками, на яких вони досягають найбільших значень:

τ₁=(σ₂ - σ₃)/2; τ₂=(σ₃ – σ₁)/2; τ₃=(σ₁ – σ₂)/2.

Якщо навантаження розподілене за смугою (теоретично нескінченної довжини), то така задача має назву двовимірної або плоскої (рис. 6.6, а). У цьому випадку складові напружень змінюються лише в напрямках двох координатних осей, зберігаючи постійне значення в напрямі однієї. У випадку дії навантаження, розподіленого за площадкою обмежених розмірів в усіх напрямах, напружений стан масиву характеризується зміною складових напружень у напрямах трьох координатних осей. На відміну від плоскої тривимірну задачу в механіці суцільного середовища називають просторовою (рис. 6.6, б).

Величини тензорів напружень і деформацій співвіднесені із системою координат х, у, z і при зміні її теж змінюються. Однак напружений стан у точці масиву як фізичний об'єкт, звичайно, не може залежати від довільної системи координат, і тому повинен мати характеристики, не залежні від неї. тобто інваріантні по відношенню до системи координат. До інваріантних характеристик напруженого стану належать, зокрема, головні площадки й головні напруження yz, які можна вказати для будь-якого тензора напружень. Три головні взаємно перпендикулярні площадки характерні тим. шо за ними діють лише нормальні напруження, а дотичні відсутні. При цьому завжди приймають, шо σ₁>σ₂>σ₃. Знаючи головні нормальні напруження, можна визначити й головні дотичні напруження, що діють за площадками, на яких вони досягають найбільших значень:

τ₁=(σ₂ - σ₃)/2; τ₂=(σ₃ – σ₁)/2; τ₃=(σ₁ – σ₂)/2.

Плоска та просторова задача для визначення напружено-деформативного стану у масивах грунту.

Якщо навантаження розподілене за смугою (теоретично нескінченної довжини), то така задача має назву двовимірної або плоскої (рис. 6.6, а). У цьому випадку складові напружень змінюються лише в напрямках двох координатних осей, зберігаючи постійне значення в напрямі однієї. У випадку дії навантаження, розподіленого за площадкою обмежених розмірів в усіх напрямах, напружений стан масиву характеризується зміною складових напружень у напрямах трьох координатних осей. На відміну від плоскої тривимірну задачу в механіці суцільного середовища називають просторовою (рис. 6.6, б).

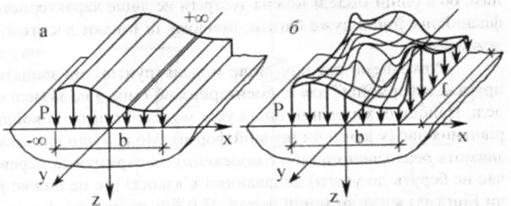
Рис. 6.6. Схеми навантажень для. а - плоскої задачі; б - просторової задачі

У класичній механіці ґрунтів для визначення напружень і деформацій застосовують теорію лінійно деформованого середовища. Для використання її висновків до будь-якого тіла необхідне додержання лінійної залежності між напруженнями та деформаціями, або підпорядкування матеріалу тіла математичній залежності, аналогічній закону Гука.

При цьому наявність властивості пружних тіл повністю відновлювати свою форму після розвантаження не обов'язкова, якщо тільки мова йде про одноразове навантаження. У теорії лінійно деформованого середовища використовують математичні залежності теорії пружності, але, на відміну від останньої, в ній розглядають непружні, лінійно деформовані тіла при їх одноразовому навантаженні. Для використання у класичній механіці грунтів апробованих розв'язань приймають деякі припущення й обмеження, як-от: розрахунки ведуть лише в інтервалі навантажень, у межах котрих грунт можна вважати лінійно деформованим, а також вважають ґрунт за суцільне, однорідне та ізотропне середовище. Не відображає теорія пружності й деформації ґрунтів у часі.

2) Визначення напружень в масиві від дії зосередженої сили.

Задача Ж.Буссінеска. Дія вертикальної зосередженої сили.

У 1885 р. французьким ученим Ж. Буссінеском була розв'язана задача про розподілення напружень у грунті при дії зосередженої сили. Задача має теоретичний і прикладний характер, ґрунт у цій задачі уявляється однорідним, ізотропним, лінійно деформованим напівпростором. що має нескінченне поширення за глибиною і за площею.

Розглянемо дію вертикальної зосередженої сили N. прикладеної у точці О до горизонтальної площини, що є поверхнею лінійно деформованого напівпростору (рис. 7.1, а). Під дією цієї сили в усіх точках напівпростору виникає складний напружений стан. У загальному випадку в кожній точці буде діяти шість складових напружень. Найбільше практичне значення мають напруження, що діють на площадках, паралельних поверхні напівпростору: σ_z, τ_xy, і τ_zx.

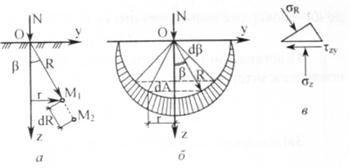
Рис. 7.1. Схеми дії сил: а - схема дії зосередженої сили; 6 - розподіл напруження на півкульовій поверхні: в -дія напруження в точці М₁.

Візьмемо довільну точку М₁ на глибині: і визначимо її положення у полярних координатах. Зрозуміло, що переміщення елементарного об'єму грунту в цій точці під дією сили N буде тим меншим, чим далі вона розташована від точки прикладання сили, тобто обернено пропорційним радіусу R. У той же час при одному й тому ж значенні R, переміщення точок будуть неоднаковими при різних значеннях кута β. Переміщення точки М₁ будуть максимальними, якщо кут β дорівнює нулю (на осі Z). При збільшенні кута β переміщення зменшуються і на поверхні грунту дорівнюють нулю (β=90⁰).

Вертикальне напруження:

,

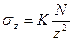де

.

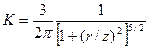Аналогічно знаходимо дотичні напруження:

,

.

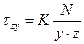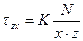Значення коефіцієнта К можна знайти в таблицях залежно від співвідношення r_i/z.

Дата добавления: 2014-01-04