Загальні види страхування життя

Розглянемо контракти страхування життя, для яких виплати змінюються з року в рік, припускаючи, що застрахована сума виплачується наприкінці року смерті. Якщо через позначено суму, яка застрахована протягом 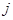-го року з моменту укладання контракту, то

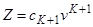. (4.1)

Розподіл 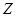і, зокрема, чисту одиночну премію, а також вищі моменти, легко підрахувати за формулою

. (4.2)

Такий контракт може бути представлений як комбінація контрактів відкладеного страхування, кожен з яких має фіксовану застраховану суму. Тоді чиста одиночна премія може бути обчислена

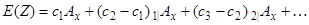. (4.3)

У випадку, коли страхування покриває тільки термін 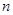років, тобто при , контракт можна також представити у вигляді комбінації контрактів термінового страхування, які вступають в силу негайно:

. (4.4)

Вирази (4.3), (4.4) можна застосовувати при обчисленні чистої одиночної премії, але не при знаходженні вищих моментів для .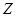

Якщо виплати за контрактом проводяться негайно в момент смерті, застрахована сума може в загальному випадку бути функцією, і тоді ми маємо

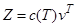. (4.5)

Чиста одиночна премія дорівнює

. (4.6)

Реально обчислення чистої одиночної премії може бути зведено до викладок по дискретній моделі, див. (4.2) у випадку 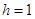. З

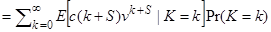
, (4.7)

маємо

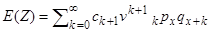, (4.8)

де вводиться позначення

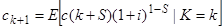. (4.9)

Умовний розподіл для 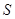, при , необхідний для обчислення виразу (4.9). Два припущення відносно смертності для дробового віку можуть бути застосовані з тією ж метою.

Ситуація А розділу 6 теми 2 дає

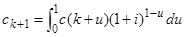, (4.10)

а ситуація Б того ж розділу приводить до співвідношення

. (4.11)

В якості ілюстрації розглянемо випадок експоненціальнозростаючої застрахованої суми 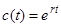. Це зводить формулу (4.10) до

. (4.12)

Зауважимо, що дає нам (3.5). Формула (4.11) зводиться до

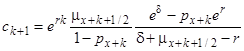. (4.13)

(якщо знаменник в (4.12) або (4.13) перетворюється в нуль, то за правилом Лопіталя дріб дорівнює 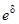. Це відповідає випадку, коли підінтегральна функція в (4.10) і (4.11) відповідно не залежить від .

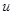Дата добавления: 2014-01-04