Виплати декілька разів на рік

Розглянемо випадок, коли виплати суми 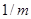проводяться 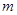разів на рік, тобто в моменти часу 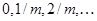, поки людина 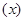жива. Чиста одиночна премія такого аннуітету позначається 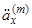. По аналогії з (2.8) ми маємо

. (3.1)

Звідси отримуємо

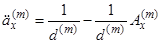. (3.2)

Це рівняння можна інтерпретувати так: Аннуітет життя, який виплачується 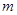разів на рік, можна розглядати як різницю двох вічних аннуітетів, які починаються в моменти 0 і 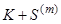. Усереднюючи, отримаємо (3.2).

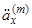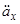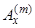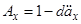Для отримання виразу через ми знову використаємо ситуацію А розділу 6 теми 2, звідки формула (3.10) теми 3 дозволяє виразити з (3.2) в термінах . Замінюючи потім , ми можемо записати (3.2) у вигляді

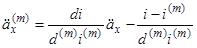. (3.3)

Ввівши позначення

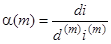и 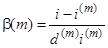, (3.4)

ми можемо записати (3.2) коротше

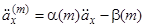. (3.5)

При 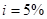коефіцієнти 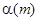і 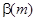протабульовані нижче для 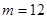(помісячні платежі) і 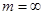(неперервні платежі).

M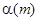
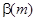
	1.000197	0.46651
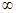
	1.000198	0.50823

Як правило використовується апроксимація

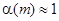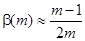, . (3.6)

Ця апроксимація отримується з розкладу ряд Тейлора коефіцієнтів в околі 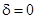, тобто

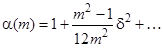, (3.7)

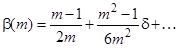. (3.8)

Очевидно, що ця апроксимація корисна тільки у випадку, коли сила відсотку достатньо мала.

Чиста одиночна премія термінового аннуітету життя pre-numerando з 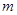платежами щорічно може бути тепер виражена з використанням 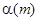і :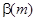

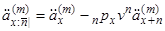
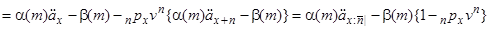. (3.9)

Чисту одиночну премію аннуітету post-numerando можна обчислити в термінах відповідних аннуітетів pre-numerando:

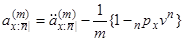. (3.10)

Повернемося до обчислення 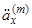. Рівняння (2.8) і (3.1) дають точне співвідношення

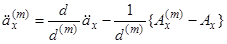, (3.11)

яке можна інтерпретувати так: Аннуітет життя з лівої сторони означає виплати суми 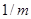в моменти часу 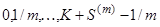і дорівнює різниці двох термінових аннуітетів, перший з виплатами в моменти 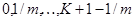, а другий – в моменти 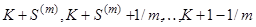. Другий терміновий аннуітет в свою чергу може розглядатися як різниця двох нескінченних аннуітетів (які починаються в моменти 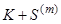і 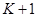). Перший терміновий аннуітет має таке ж поточне значення, як аннуітет pre-numerando з 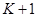щорічними виплатами сумі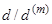. Усереднюючи ці поточні значення, отримуємо (3.11).

При ситуації А використання (3.10) дає

. (3.12)

Ця формула має очевидну інтерпретацію, на відміну від математично еквівалентної формули (3.5).

Дата добавления: 2014-01-04