Контракти з поверненням премії

В практичному страхуванні зустрічається велика різновидність форм страхування і видів преміальних платежів. Це робить нереальним отримання явного запису чистої одиночної премії для кожної можливої комбінації. Головне правило в цій ситуації – необхідно скласти збиток страхувальника 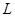, а потім застосувати умову (1.1). Проілюструємо цю процедуру таким прикладом.

Маємо контракт чистого дожиття з одиничною застрахованою сумою, яка виплачується після закінчення 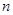років, з поверненням виплаченої премії (без відсотків) у випадку смерті до терміну закінчення контракту. Яка повинна бути чиста річна премія, якщо фактично премія, яка знімається із застрахованого, перевищує чисту річну на 40% (40%-ва надбавка застосовується для покриття витрат)?

Позначимо чисту річну премію через 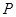. Збиток страхувальника дорівнює, очевидно,

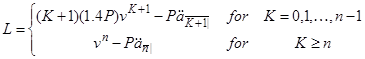. (6.1)

Очікуваний збиток дорівнює

, (6.2)

і застосування (1.1) дає співвідношення для премії

. (6.3)

7. Випадкова (стохастична) відсоткова ставка

Відсоткова ставка, яка застосовується до майбутнього, звичайно, завчасно невідома. Тому природньо поставити питання чому майбутні відсоткові ставки не розглядаються як стохастичний процес. Така модель не розглядається з двох причин.

1. Страхування життя як правило проводиться на великий термін, і загальноприйнятої стохастичної моделі, яка передбачає зміни відсоткової ставки на великий термін, не існує;

2. Логічно припустити, що терміни життя майбутнього життя застрахованих є, взагалі кажучи, незалежними випадковими величинами. При прийнятті гіпотези про фіксовану відсоткову ставку збитки страхувальника за різними контрактами стають незалежними випадковими величинами. Розподіл імовірності для сумарного збитку в цьому випадку може бути отриманий конволюцією. Зокрема, варіація сумарного збитку дорівнює сумі індивідуальних варіацій, що полегшує використання апроксимації нормальним розподілом. Стохастична незалежність контрактів може бути втрачена з введенням стохастичної відсоткової ставки, оскільки всі контракти в однаковій мірі перебувають під впливом зміни відсоткової ставки.

Тому ми будемо, як і раніше, використовувати гіпотезу про фіксовану відсоткову ставку. Практична оцінка страхового покриття повинна включати в себе аналіз різних сценаріїв зміни відсоткової ставки.

Дата добавления: 2014-01-04