Обертальний рух твердого тіла навколо нерухомої осі

Контрольні запитання

1. Який рух твердого тіла називається поступальним? Наведіть приклавди такого руху.

2. Які траєкторії мають точки твердого тіла, що здійснює поступальний рух?

3. Які основні властивості твердого тіла, що здійснює поступальний рух?

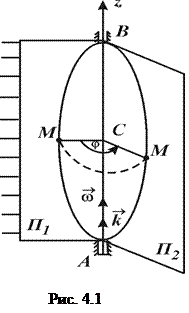Обертальним рухом твердого тіла навколо нерухомої осі називається такий, при якому всі його точки рухаються по концентричним колам, центри яких лежать на нерухомій прямій, яка. називаєтьсявіссю обертання. У цьому випадку всі точки, крім тих, що лежать на осі обертання, здійснюютьрух в площинах, перпендикулярних до осі обертання.

Для визначення положення тіла направимо вісь 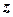вздовж осі обертання 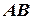(вгору). Зв’яжемо з довільною точкою М твердого тіла та віссю обертання площину 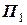і зафіксуємо її положення (рис. 4.1) в нерухомій системі координат. Через деякий час тверде тіло повернеться на кут 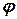і площина займе положення 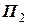(рис. 4.1). Тоді положення тіла буде однозначно заданим, коли відомий закон зміни кута

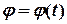(4.1)

між зафіксованою площиною 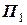та рухомою площиною 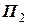. Цей кут називається кутом повороту тіла.

Головними кінематичними характеристиками обертального руху тіла є кутова швидкість (яке характеризує швидкість зміни кута повороту з плином часу) та кутове прискорення (яка характеризує зміну кутової швидкості з плином часу).

Вектором кутової швидкості 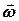твердого тіла, яке здійснює обертання навколо фіксованої осі, називається вектор, модуль якого дорівнює абсолютному значенню похідній по часу від кута повороту

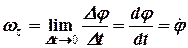, (4.2)

та напрямлений вздовж осі обертання в ту сторону (рис. 4.1), звідки обертання відбувається проти руху стрілки годинника

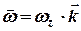, (4.3)

де 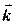- орт осі 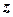, з якою співпадає вісь обертання (рис. 4.1). З формули (4.3) видно, що напрям вектора 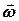співпадає з напрямом вектора 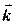, якщо 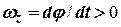, та напрямок вектора 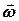протилежний напряму вектора 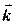, якщо .

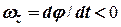Вектором кутового прискорення називається вектор, який дорівнює похідній по часу від вектора кутової швидкості

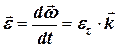. (4.4)

Друга похідна по часу від кута повороту визначає алгебраїчне значення кутового прискорення

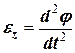. (4.5)

Якщо вісь обертання зафіксована, то напрям 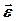співпадає з напрямом 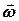коли модуль кутової швидкості 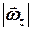зростає (обертання тіла прискорене), то напрям вектора 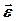співпадає з напрямом вектора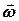і напрям 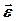буде протилежним напряму 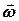, коли модуль кутової швидкості 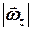зменшується (обертання тіла буде сповільненим). З цих обставин випливає наступне просте правило: якщо алгебраїчний добуток 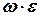> 0, то обертальний рух твердого тіла прискорений, якщо 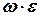< 0 – сповільнений.

Зауважимо, що вектори кутової швидкості та кутового прискорення завжди розташовані на осі обертання.

Зв’язок кутових та лінійних кінематичних величин

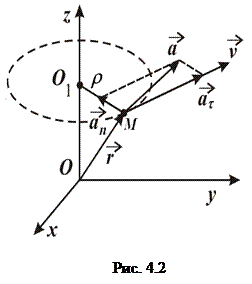
Лінійна швидкість довільної точки 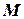твердого тіла, яке обертається навколо нерухомої осі 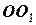(рис. 4.2), визначається векторним добутком вектора кутової швидкості 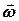на радіус-вектор 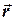цієї точки відносно довільної точки 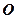, що лежить на осі обертання, і не залежить від вибору цієї точки.

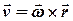(4.6)

Модуль лінійної швидкості дорівнює

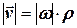, (4.7)

де 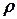= 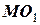– віддаль від точки 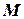до осі обертання (дивись рис. 4.2).

Тангенціальне та нормальне прискорення точки 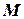твердого тіла визначаються формулами:

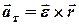, (4.8)

. (4.9)

Модулі тангенціального, нормального та повного прискорень залежать від віддалі точки до осі обертання 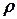і можуть бути обчислені за формулами:

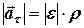, (4.10)

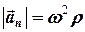, (4.11)

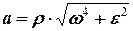. (4.12)

Дата добавления: 2014-01-04