Плоский рух твердого тіла

Плоским (чи плоскопаралельним) рухом називається такий рух твердого тіла, при якому всі точки тіла рухаються в незмінних площинах, паралельних 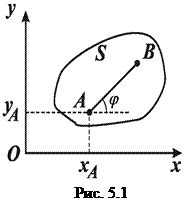до деякої нерухомої площини , яка носить назву основної. Отже, плоский рух твердого тіла можна звести до вивчення руху плоскої фігури 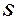, утвореної перетином тіла площиною (рис. 5.1). Щоб описати плоский рух твердого тіла, потрібно задати дві поступальні і одну обертальну координати. 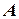Як правило, використовують дві декартові координати (, ) довільної точки плоскої фігури (цю точку називають полюсом) і кут 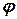, який утворює відрізок 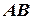, що лежить в площині фігури та з’єднує полюс і довільну точку 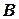, з віссю (рис. 5.1). При русі плоскої фігури 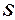в своїй площині величини 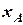, і 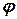змінюються з часом:

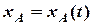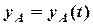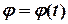, , . (5.1)

Перші два рівняння визначають поступальний рух полюса, а третє – рівняння обертання плоскої фігури навколо полюса.

Швидкість довільної точки 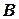фігури, яка здійснює плоский рух, визначається за формулою

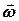
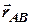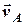+ = + , (5.2)

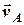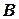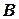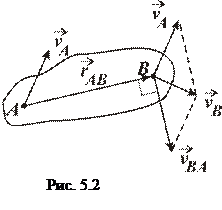
де - поступальна швидкість полюса (точки А), - швидкість точки в її обертальному русі разом з плоскою фігурою навколо цього полюса. Отже, швидкість довільної точки зображається діагоналлю паралелограма, побудованого в точці 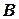на векторах 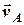і (рис. 5.2).

При плоскому русі фігури, якщо її кутова швидкість не дорівнює нулю (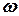≠ 0), в кожний момент часу існує єдина точка в цій площині, навколо якої фігура здійснює чисто обертальний рух. Ця точка називається миттєвим центром швидкостей (МЦШ) і, як правило, позначається буквою 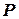. Якщо ця точка належіть твердому тілу, то абсолютна швидкість цієї точки тіла в даний момент часу дорівнює нулю.

Якщо вибирати полюс у миттєвому центрі швидкостей 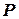, то модуль швидкості довільної точки 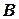плоскої фігури визначається формулою

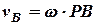, (5.3)

і лінійна швидкість точки 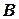направлена перпендикулярно до прямої 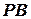(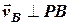) за напрямом обертання фігури (рис. 5.3, 5.4).

Отже, плоскопаралельний рух твердого тіла в кожний момент часу можна розглядати як безперервну послідовність нескінченно малих поворотів навколо миттєвого центру обертання. Зауважимо, що положення миттєвого центру швидкостей може змінюватись з плином часу.

Основні методи знаходження МЦШ

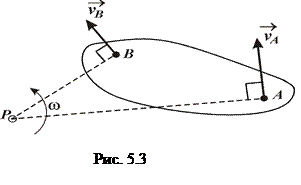
1. Якщо відомі напрями швидкостей двох точок твердого тіла, що здійснює плоский рух, то МЦШ знаходимо шляхом встановлення перпендикулярів до векторів швидкостей у точці перетину цих перпендикулярів (рис. 5.3).

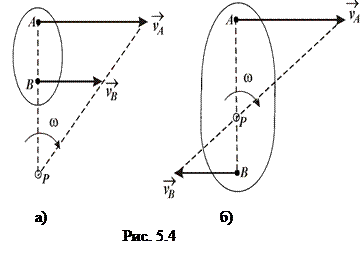2. Якщо вектори швидкостей паралельні (рис. 5.4), то МЦШ лежить на відрізку прямої, що з’єднує ці точки та ділить його на частини пропорційні величинам швидкостей

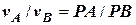(5.4)

зовнішнім чином (рис. 5.4 а), коли вектори спрямовані в одну сторону, та внутрішнім чином (рис. 5.4 б), коли напрями векторів швидкості проти-лежні.

Для визначення прискорення довільної точки твердого тіла при плоскому русі візьмемо похідну від правої та лівої частин векторного рівняння (5.2), що визначає швидкість довільної точки 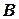плоскої фігури і отримуємо

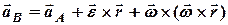, (5.5)

де 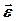– вектор кутового прискорення плоскої фігури.

Введемо позначення:

= , (5.6)

= , (5.7)

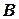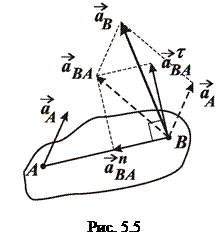
Вектори і визначають відповідно тангенціальне і нормальне прискорення точки при обертальному русі фігури навколо полюса 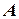(рис. 5.5). Вектор нормального (доцентрового) прискорення , завжди направлений від точки 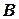до полюсу (точки 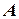в нашому прикладі). Вектор тангенціального (обертального) прискорення , перпендикулярний до 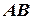і напрямлений по вектору швидкості обертального руху точки 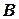навколо полюса 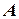, коли обертання прискорене та проти цієї швидкості, коли обертання сповільнене. Векторна сума цих двох доданків є прискоренням точки 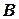при обертанні фігури навколо полюса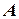

. (5.8)

Вектори і взаємно перпендикулярні, тому модуль прискорення обертального руху

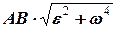= . (5.9)

Отже, прискорення довільної точки (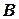) плоскої фігури дорівнює векторній сумі прискорення полюса і прискорення () точки 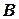в її обертальному русі разом з фігурою навколо полюса

. (5.10)

Дата добавления: 2014-01-04