Вбудовані (inline) функції, порівняння з макровизначеннями, закриті функції

Вбудовані (inline) функції

Функції

Процедурно-орієнтоване програмування

А взявши програму логарифмічного степеню, можна обчислювати числа Фібоначчі з логарифмічною складністю (подумайте, як?)

void zet(double &y, double &x, int &k)

{

if (k)

{

if (k%2)

{

y*=x; k--;

}

else

{

x*=x; k/=2;

};

zet(y,x,k);

}

}

double power(double x, int n)

{

double y =1;

zet(y, x, n);

return y;

}

Існують, правда, задачі, складність яких не усувається, наприклад, знамениті Ханойські вежі

void Hanoi(int n, char a, char b, char c)

{

if (n)

{

Hanoi(n-1,a,c,b);

cout<<”from ”<<a<<”to ”<<b<<endl;

Hanoi(n-1,c,b,a);

}

}

Зміст визначення функції очевидний. Це повна характеристика її типу і її параметрів разом із повним текстом її команд, що служать реалізацією функції, наприклад,

int gcd (int m, int n)

{

while (m!= n)

if m>n m=m-n; else n=n-m;

// m == n

return m;

}

достатню для того, щоб компілятор побудував об'єктний код функції.

Кожна функція визначається один раз, а використовується багато разів у різних файлах. Для компіляції викликів компілятору досить мати лише інформацію про кількість і типи параметрів, а також тип результату. Сам код тепер непотрібен. Він буде потрібен лише компонувальнику. Тому користуються оголошенням функції, яке ще називають її сигнатурою. Ось сигнатура попередньої функції

int gcd (int m, int n);

або навіть

int gcd (int, int);

яка читається так: ціла функція двох цілих параметрів. В цьому випадку виконання функції повинне закінчуватись командою виходу, параметром якої служитиме цілий вираз. Його значення і є результатом виконання функції.

Функція може не повертати значення. В цьому випадку її сигнатура починається словом void.

За способом виклику розрізняють функції відкриті і закриті. Вбудовані функції можна уявляти собі як багатократне повторення тексту функції по одній в кожному місці виклику. Так вхідний текст

z1 = gcd (x1, y1);

z2 = gcd (x2, y2);

в об'єктному коді перетвориться в щось на зразок

// z1 = gcd (x1, y1);

m = x1; n = y1;

while (m!= n)

if m>n m=m-n; else n=n-m;

z1 = m;

// z2 = gcd (x2, y2);

m = x2; n = y2;

while (m!= n)

if m>n m=m-n; else n=n-m;

z2 = m;

Тут синім кольором позначена передача значень фактичних параметрів формальним, а зеленим повернення результатів.

Компілятору можна дати підказку реалізувати функцію вбудованим способом

inline int gcd (int m, int n)

{

while (m!= n)

if m>n m=m-n; else n=n-m;

// m=n

return m;

}

Дуже схожим до вбудованих функцій є механізм макровизначень. Різниця полягає лише в реалізації підготовчих дій.

Оскільки макровизначення обробляється макропроцесором, то обробка полягає у підстановці тексту фактичних параметрів на місце формальних.

Розглянемо простий приклад функції

int square (int a)

{

return (a*a);

}

ЇЇ виклик y=square(x) перетвориться на команди

a=x;

y=a*a;

В той час як макровизначення

# define square (a) ((a) * (a))

приведе до тексту

y=(x)*(x);

на перший погляд коректного і навіть простішого.

Тепер розглянемо виклик

x = 1;

y=square(++x);

Використання функції дасть очікуваний результат

x = 1;

a=++x; // a == 2;

y=a*a; // y == 4, x == 2

тоді як з використанням макро матимемо дещо несподіваний результат

y=(++x)*(++x); // y == 9; x == 3

Справа в тому, що текстова підстановка параметрів не зовсім коректна, оскільки обчислення параметру може мати сторонній ефект. Проаналізуйте результати у випадку виклику y=square(x++);

І нарешті звичайний спосіб, відомий під назвою закритих процедур. Закритих тому, що для функції виготовляється окремий об’єктний код. Виклик функції проходить у такій послідовності. Спочатку обчислюються значення параметрів, запам’ятовується місце, з якого почнеться продовження обчислень після повернення з підпрограми. Далі виконується команда так званого переходу до підпрограми. Після виконання підпрограми відбувається повернення результату і передача керування в місце продовження обчислень. Умовно ця послідовність зображена на малюнку. Реально виклик відбувається дещо складніше оскільки в місці виклику невідомі імена параметрів (кажуть, що вони локалізовані в функції), а функцій не знає місця призначення результату. Тому в передачі бере участь ще одна допоміжна ланка — стек.

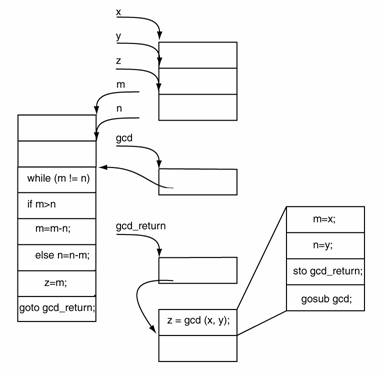
Тому насправді присвоєння формальним параметрам значень фактичних, наприклад, m=x відбувається розподілено: в місці виклику виконується команда покласти значення цілого виразу x до стеку, а в підпрограмі — команда дістати зі стеку ціле число та присвоїти його формальному параметру m. Так само повернення результату починається із запису значення формального параметра m в стек, а в місці повернення після виклику ціле число забирається зі стеку і присвоюється z.

Дата добавления: 2014-01-04