
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекція 3
|
|
|
|
Самостійно
9.2. Аналіз енергетичних характеристик методом контурних інтегралів
9.2.1. Загальні співвідношення
Припустимо, що характеристика нелінійної системи допускає представлення контурним інтегралом

 - реакція нелінійної системи на вплив білого шуму.
- реакція нелінійної системи на вплив білого шуму.
Скористаємося формулою для кореляційної функції випадкового процесу на виході нелінійної системи, за умови, що на її вхід діє випадковий процес (суміш детермінованого сигналу  і гаусівського центрованого стаціонарного процесу з дисперсією
і гаусівського центрованого стаціонарного процесу з дисперсією 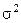 і нормованою кореляційною функцією
і нормованою кореляційною функцією 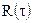 ).
).

У цьому інтегралі тільки множник 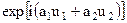 залежить від часу (
залежить від часу (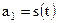 і
і 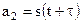 ). Тому при усередненні в часі кореляційної функції
). Тому при усередненні в часі кореляційної функції 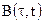 усереднюється тільки цей множник. Позначаючи
усереднюється тільки цей множник. Позначаючи

Знаходимо усереднену кореляційну функцію випадкового процесу на виході нелінійної системи

Розглянемо випадок, коли  . Знаходимо
. Знаходимо
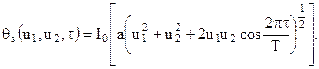
На основі відомої в теорії функції Бесселя теореми додавання, можна представити у виді ряду

де 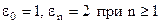 .
.
Підставляючи цей вираз у вираз для усередненої функції і з огляду на те, що
 ,
,
виходить можливим розділити перемінні інтегрування і представити усереднену за часом кореляційну функцію у виді:
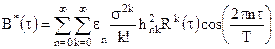 , (9.6)
, (9.6)
де


У (9.6) група членів, для яких k=0, відповідає дискретній частини цього спектра на частоті 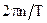 . Інші члени при
. Інші члени при 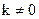 відповідають неперервній частині спектра.
відповідають неперервній частині спектра.
Якщо в (9.7) покласти, що а=0, то знайдемо кореляційну функцію процесу на виході нелінійної системи, коли на її вхід діє стаціонарний гаусівський процес. У цьому випадку  і
і
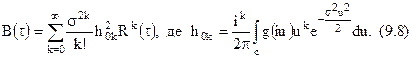
Зазначимо, що якщо в 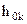 замінити g(iu) його інтегральним перетворенням
замінити g(iu) його інтегральним перетворенням
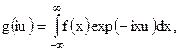 а також скористатися співвідношенням
а також скористатися співвідношенням
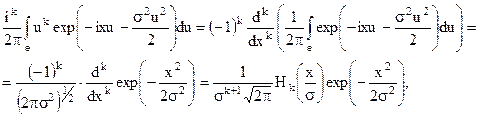
то можна переконатися, що величина 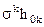 в розкладанні (9.8) збігається з коефіцієнтом
в розкладанні (9.8) збігається з коефіцієнтом 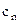 у розкладанні отриманим прямим методом.
у розкладанні отриманим прямим методом.
З (9.6) видно, що визначення спектральної щільності потужності суми періодичного сигналу і стаціонарного гаусівського процесу після нелінійного перетворення зводиться до обчислення перетворення Фур'є від ступенів нормованої кореляційної функції гаусівського процесу й інтегралів (9.7) які залежать тільки від характеристики g(iu) нелінійної системи.
9.3. Аналіз енергетичних характеристик методом похідних
Самостійно
9.3.1. Загальні співвідношення
Характеристика нелінійної системи y=f(x) на вході системи сума детермінованого процесу і стаціонарного центрованого гаусівського процесу 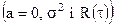 . У випадку визначення кореляційної функції процесу на виході системи методом похідних, має значення залежність кореляційної функції процесу на виході системи від
. У випадку визначення кореляційної функції процесу на виході системи методом похідних, має значення залежність кореляційної функції процесу на виході системи від 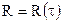 , що позначимо B(R). Знаходимо
, що позначимо B(R). Знаходимо

Для того, щоб проінтегрувати це рівняння необхідно задати k граничних умов. Такими умовами є значення функції B(R) і її похідних по R до (k-1)-го порядку при R=0 (тобто при 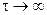 ) чи при R=1 (тобто при
) чи при R=1 (тобто при  ). З (9.10) безпосередньо одержимо
). З (9.10) безпосередньо одержимо
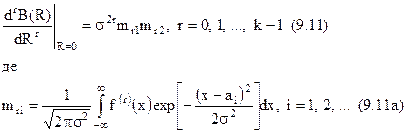
Якщо  і з (9.10) випливає
і з (9.10) випливає
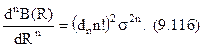
У цьому випадку кореляційна функція процесу, що виникає після нелінійного перетворення гаусівського процесу, представляє поліном n-ї степені від 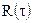 . Так використовуючи (9.11 б) неважко одержати формулу для двопівперіодного квадратичного детектора
. Так використовуючи (9.11 б) неважко одержати формулу для двопівперіодного квадратичного детектора 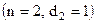 при граничних умовах
при граничних умовах 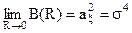 і
і .
.
Нехай функція f(x) складена з кусків поліномів, що утворять у місцях стику кутові точки. Тоді при досить великому k похідна  буде дорівнювати сумі дельта-функцій і обчислення інтеграла (9.10) стає елементарним, якщо скористатися фільтруючою властивістю дельта функції і її похідних.
буде дорівнювати сумі дельта-функцій і обчислення інтеграла (9.10) стає елементарним, якщо скористатися фільтруючою властивістю дельта функції і її похідних.
Лекція 8
Тема: Проходження нормального випадкового процесу через типову ланку радіотехнічних пристроїв.
1. Постановка задачі.
Характерним для багатьох етапів роботи радіотехнічних пристроїв є перетворення сигналів, що представляють випадкові процеси, у типовій ланці, що складається із трьох послідовних елементів: вхідної лінійної системи, нелінійного (неінерційного) елемента і вихідної лінійної системи.
Якщо на вході типової ланки діє нормальний випадковий процес, то знаходження енергетичного спектра на його виході не має принципових труднощів. Після вхідної лінійної системи процес залишається нормальним, а спектр деформується відповідно до форми частотної характеристики цієї лінійної системи. У результаті нелінійного перетворення функції розподілу процесу перестають бути нормальними, але спектр перетвореного процесу можна визначити, користуючись одним з методів, викладених у лекціях 1, 2, 3 за ці семестри.
Однак у багатьох випадках знання енергетичного спектра процесу на виході типової ланки виявляється недостатнім, необхідно знати функції розподілу, знаходження яких зв'язано зі значними утрудненнями, тому що для цього необхідно вирішувати задачу про перетворення функції розподілу випадкового процесу в лінійній системі, коли процес, що діє на її вході, не є нормальним.
Якщо ж процес на вході типової ланки не є нормальним, то ця проблема з'являється вже на першому етапі дослідження. Відомо лише кілька точних рішень задачі про визначення функцій розподілу процесу на виході типової ланки.
Наближений метод визначення одномірної функції розподілу полягає в обчисленні деякого числа моментів розподілу. Однак \\\\\\\\\\\\ використання цього методу зв'язано з трудомісткими розрахунками.
Надалі розглянемо точні і наближені методи рішення наступних типів задач про визначення одномірної функції розподілу процесу на виході типової ланки.
1. Випадковий процес на вході ланки представляє суму детермінованого сигналу і стаціонарного випадкового процесу з рівномірним спектром («білий шум»), а характеристика нелінійного елемента квадратична. У цьому випадку розглянута задача збігається з наступною радіотехнічною задачею.
На вході підсилювача проміжної частоти (ППЧ) діє детермінований сигнал і шум. Сигнал із шумом піддаються квадратичному детектуванню і наступній фільтрації. Яка функція розподілу сигналу і шумів на виході фільтра?
2. На вході фільтра діє добуток двох корельованих стаціонарних нормальних випадкових процесів. Необхідно визначити функцію розподілу процесу на виході фільтра. До рішення цієї задачі зводиться дослідження розподілу процесу на виході корелятора при кінцевому часі інвертування, тобто величини 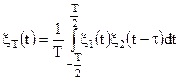 , якщо
, якщо  - стаціонарні нормальні випадкові процеси.
- стаціонарні нормальні випадкові процеси.
2. Типова ланка: підсилювач-квадратичний детектор-фільтр
2.1. Рішення задачі при широкосмуговому підсилювачі
Нехай лінійні системи розглянутої типової ланки характеризуються своїми імпульсними перехідними функціями: ППЧ-функцією  і фільтруючою функцією
і фільтруючою функцією  . Позначимо через s(t) – детермінований сигнал і
. Позначимо через s(t) – детермінований сигнал і 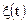 - білий нормальний шум, що діють на вході ППЧ. Так як при проходженні через лінійну систему сигнал і шум не взаємодіють, то процес на виході ППЧ буде сумою двох доданків
- білий нормальний шум, що діють на вході ППЧ. Так як при проходженні через лінійну систему сигнал і шум не взаємодіють, то процес на виході ППЧ буде сумою двох доданків  . Представимо кожне з них у виді інтегралів:
. Представимо кожне з них у виді інтегралів:

Представимо квадрат випадкового процесу на виході ППЧ у наступному виді:

Позначимо через  процес на виході типової ланки тобто після фільтра
процес на виході типової ланки тобто після фільтра

Підставляючи (13.3) у (13.4) і провівши заміну змінних  , одержуємо
, одержуємо
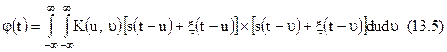
де
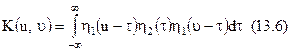
Вираз (13.5) представляє те шукане інтегральне перетворення, яким зв'язаний процес на виході типової ланки з процесом на його виході. Функцію  залежну тільки від характеристик ППЧ і фільтра називаються ядром цього перетворення.
залежну тільки від характеристик ППЧ і фільтра називаються ядром цього перетворення.
Тобто рішення поставленої задачі зводиться до визначення ймовірнісних характеристик інтеграла (13.5).
Так як ядро перетворення 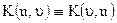 , тобто симетричне, то його можна розкласти в ряд по ортогональних функціях
, тобто симетричне, то його можна розкласти в ряд по ортогональних функціях

де  - власні функції (розв’язки) і власні (характеристичні числа) однорідного інтегрального рівняння
- власні функції (розв’язки) і власні (характеристичні числа) однорідного інтегрального рівняння
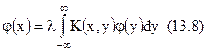
ядро якого K(x, y) виражене через імпульсні перехідні функції ППЧ і фільтра (див. 13.6)
Після підстановки (13.7) у (13.5) одержимо
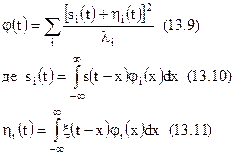
Як видно з рівняння (13.9), задача вивчення ймовірнісних характеристик випадкового процесу 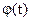 на виході типової ланки зводиться до визначення функцій розподілу суми квадратів випадкових процесів
на виході типової ланки зводиться до визначення функцій розподілу суми квадратів випадкових процесів 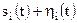 , де
, де 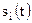 детерміновані. За умовою задачі випадковий процес
детерміновані. За умовою задачі випадковий процес 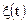 – нормальний, тому випадкові процеси
– нормальний, тому випадкові процеси 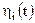 , що представляють інтеграли від
, що представляють інтеграли від 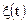 також нормальні.
також нормальні.
Розв’язання представленої задачі обмежується визначенням тільки одинарної функції розподілу. Тому достатньо усі подальші дослідження проводити в довільні, але фіксовані моменти часу. Випадкові величини  некорельовані, а отже (у силу їхнього нормального розподілу) незалежні.
некорельовані, а отже (у силу їхнього нормального розподілу) незалежні.
Сумісний розподіл незалежних нормальних випадкових величин 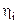 дорівнює добутку
дорівнює добутку

Розподіл суми нерівних випадкових величин відрізняється від нормального. Тому визначимо спочатку характеристичну функцію
 (13.13)
(13.13)
Шукана одномірна функція розподілу випадкового процесу 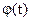 на виході фільтра отримується з (13.13) зворотним перетворенням Фур'є.
на виході фільтра отримується з (13.13) зворотним перетворенням Фур'є.
Якщо сигнал відсутній, то  і з (13.13) з урахуванням перетворень одержуємо
і з (13.13) з урахуванням перетворень одержуємо
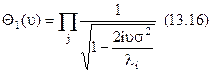
2.2. Розв’язання задачі при вузькосмуговому підсилювачі
Цей випадок відрізняється від попереднього тим, що після детектора відфільтровується високочастотна частина процесу і на відеофільтр подається квадрат обвідної суми процесів  .
.
Представимо вузькосмуговий нормальний випадковий процес на виході ППЧ у виді суми:
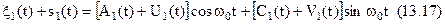
де 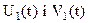 - квадратурні складові сигналу
- квадратурні складові сигналу 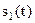 , а
, а 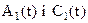 - незалежні нормально розподілені квадратурні складові шуму
- незалежні нормально розподілені квадратурні складові шуму 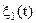 .
.
Процес на виході відеофільтра може бути представлений у цьому випадку у виді двох незалежних доданків:

Ядро інтегрального перетворення (13.5) і інтегрального рівняння (13.8) запишеться у виді:

де 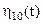 - обвідна імпульсної перехідної функції вузькосмугового ППЧ.
- обвідна імпульсної перехідної функції вузькосмугового ППЧ.
Представимо кожне з доданків (13.18) сумою у виді (13.9) і позначаючи
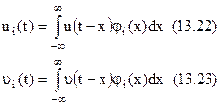
за аналогією з (13.15) одержимо наступний вираз для характеристичної функції квадрата обвідної після проходження її через відеофільтр

чи

Зворотним перетворенням Фур'є знаходимо з (13.25) одномірну функцію розподілу на виході типової ланки. Якщо сигнал відсутній, то  з (13.25) випливає
з (13.25) випливає
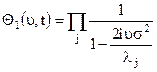
Так само як і в попередньому випадку для одержання розподілу в явному виді необхідно розв’язати інтегральне рівняння (13.8) для того, щоб визначити величини  і
і 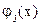 , що містяться в (13.25) (що входять через
, що містяться в (13.25) (що входять через 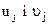 ).
).
2.2.3. Наближений метод визначення функції розподілу
Розв’язання інтегрального рівняння (13.8) є в загальному випадку досить трудомісткою операцією. Тому розглянемо наближений метод безпосереднього визначення функції розподілу процесу на виході фільтра, минаючи при цьому рішення інтегрального рівняння (13.8).
Будемо розглядати як числові характеристики випадкового процесу на виході фільтра не моменти, а кумулянти (семиінваріанти) одномірного розподілу.
Кумулянт n-го порядку дорівнює:

З (13.16) знаходимо
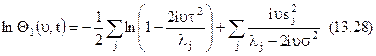
Послідовним диференціюванням визначається кумулянт n-го порядку випадкового процесу на виході фільтра

Аналогічно може бути знайдений кумулянт квадрата обвідної, що пройшла через фільтр
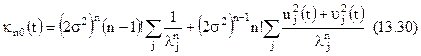
Якщо сигнал відсутній 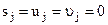 , то
, то
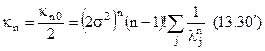
Щоб виключити власні числа  в отриманих виразах (13.29) і (13.30) ряди можуть бути виражені через інтегрування ядра
в отриманих виразах (13.29) і (13.30) ряди можуть бути виражені через інтегрування ядра  . Інтегроване ядро
. Інтегроване ядро  виходить з основного ядра
виходить з основного ядра  шляхом (n-1)-кратного інтегрування.
шляхом (n-1)-кратного інтегрування.
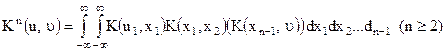
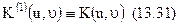
З врахуванням (13.31) одержуємо

чи

Підставляючи (13.32) і (13.33) у (13.29) знаходимо
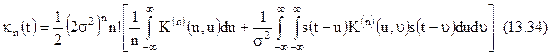
У такий спосіб можемо визначити кумулянти на виході фільтра без розв’язання інтегрального рівняння.
Вираз для кумулянта профільтрованого квадрата обвідної:
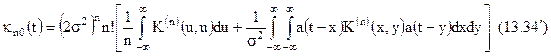
Якщо сигнал відсутній, то подвійні інтеграли зникають. Взагалі кумулянти перших двох порядків будуть рівні:
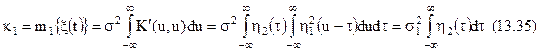
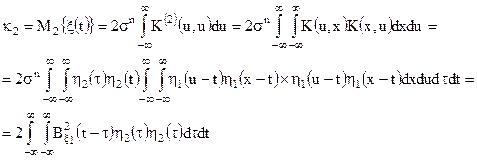
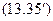
Як же користуватися отриманою кількістю кумулянтів для наближеного визначення одномірної функції розподілу. Для цього представляють шукану функцію розподілу у виді розкладання по заданих ортогональних функціях, коефіцієнти якого виражаються через кумулянти розподілу. Як систему ортогональних функцій при розкладанні приймають звичайно функції  і її похідні.
і її похідні.
Нехай  - шукана функція розподілу випадкового процесу на виході фільтра, а
- шукана функція розподілу випадкового процесу на виході фільтра, а - перші чотири кумулянти цього розподілу. Тоді перші чотири члени розкладання
- перші чотири кумулянти цього розподілу. Тоді перші чотири члени розкладання  в ряд мають вид
в ряд мають вид
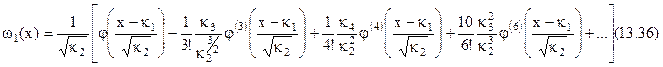 де
де  - коефіцієнти асиметрії й ексцесу відповідно розподілені
- коефіцієнти асиметрії й ексцесу відповідно розподілені  .
.
4. Типова ланка: перемножувач-фильтр
3.1. Точне розв’язання
Розглянемо два стаціонарних і стаціонарно зв'язаних нормальних випадкових процеси 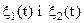 , середні значення яких нульові, а кореляційні і взаємно кореляційні функції рівні відповідно
, середні значення яких нульові, а кореляційні і взаємно кореляційні функції рівні відповідно 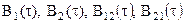 . Добуток цих процесів
. Добуток цих процесів 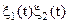 проходить через лінійну систему (фільтр) з імпульсною перехідною характеристикою h(t).
проходить через лінійну систему (фільтр) з імпульсною перехідною характеристикою h(t).
Знайдемо одномірну функцію розподілу випадкового процесу  на виході фільтра. Випадковий процес
на виході фільтра. Випадковий процес 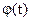 можна представити у виді
можна представити у виді
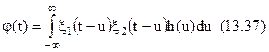
Цей інтеграл можна звести до різниці інтегралів, якщо замість 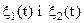 увести їхню напівсуму і напіврізницю:
увести їхню напівсуму і напіврізницю:
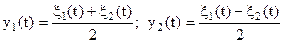
Випадкові процеси  також будуть розподілені нормально з нульовими середніми, а їх кореляційні і взаємні кореляційні функції рівні:
також будуть розподілені нормально з нульовими середніми, а їх кореляційні і взаємні кореляційні функції рівні:
 (13.38)
(13.38)
Підставляючи в (13.37) замість 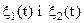 суму і різницю
суму і різницю  одержуємо
одержуємо

У такий спосіб задача зводиться до знаходження розподілу інтегралів від квадратів нормального випадкового процесу.
Характеристична функція процесу  на виході фільтра має вид:
на виході фільтра має вид:
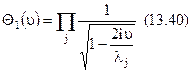
Відмінність полягає в тому, що власні числа знаходяться не з одного рівняння, а із системи двох лінійних неоднорідних інтегральних рівнянь
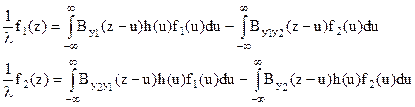 (13.41)
(13.41)
3. Приклад розрахунку для гаусівських частотних характеристик
Розглянемо приклад розрахунку функції розподілу випадкового процесу на виході типової ланки Ппч-кв. дет.-Вд. ф.
Нехай частотні характеристики ППЧ і фільтра описуються гаусівськими кривими:
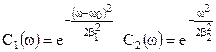
Відповідні їм імпульсні перехідні функції мають вид

Параметри  виражаються через смуги пропуску ППЧ і фільтра в такий спосіб:
виражаються через смуги пропуску ППЧ і фільтра в такий спосіб:
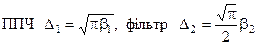
Введемо для відношення цих параметрів наступне позначення:
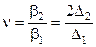
Знайдемо ядро  підстановкою в (13.6) приведених виражень для
підстановкою в (13.6) приведених виражень для 
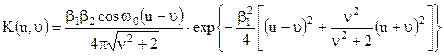
Ітероване ядро другого порядку буде дорівнювати
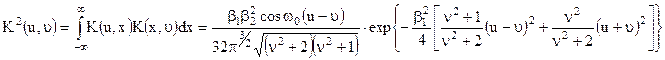 Аналогічно ітероване ядро третього порядку
Аналогічно ітероване ядро третього порядку

Для значень 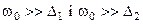 знаходимо
знаходимо
 .
.
Припустимо, що детермінована частина процесу на вході типової ланки представляє гармонічний сигнал з постійною амплітудою  (частота
(частота  збігається з резонансною частотою ППЧ) тоді будемо мати:
збігається з резонансною частотою ППЧ) тоді будемо мати:
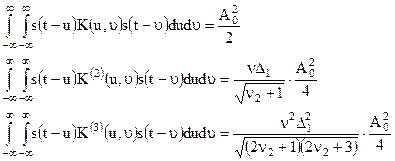
Підставляємо отримані вирази в (13.34) і позначаючи 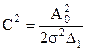 , знаходимо кумулянти перших трьох порядків випадкового процесу на виході відеофільтра.
, знаходимо кумулянти перших трьох порядків випадкового процесу на виході відеофільтра.
Кумулянт першого порядку (середнє значення) дорівнює:
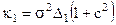
Кумулянт другого порядку (дисперсія) дорівнює
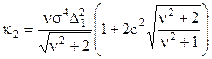
Кумулянт третього порядку (центральний момент третього порядку) дорівнює

Коефіцієнт асиметрії одномірної функції розподілу випадкового процесу на виході фільтра дорівнює:
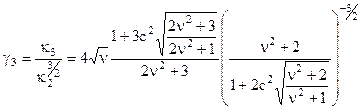
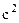 - відношення потужності сигналу до потужності шумів на виході УПЧ.
- відношення потужності сигналу до потужності шумів на виході УПЧ.
Кумулянт більш високого порядку можна обчислити по формулі:
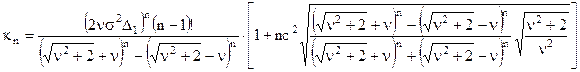
Маючи величини кумулянтів і використовуючи розкладання в ряд по ортогональних функціях, можна з заданою точністю побудувати функцію розподілу випадкового процесу на виході відеофільтра.
5. Наближене рішення для RC-фільтра
Нехай на перемножувач подається білий нормальний шум з кореляційною функцією
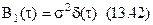
і нормальний стаціонарний випадковий процес з кореляційною функцією
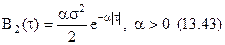
і нехай взаємні кореляційні функції цих процесів відповідно рівні
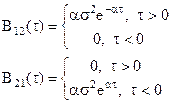 (13.44)
(13.44)
Припустимо, що лінійна система після перемножувача представляє RC-фільтр, імпульсна перехідна характеристика якого наступна,
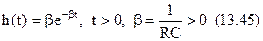
Величини  пропорційні відповідно ширині смуги процесу на вході перемножувача і ширині смуги фільтра.
пропорційні відповідно ширині смуги процесу на вході перемножувача і ширині смуги фільтра.
Заміняємо в системі інтегральних рівнянь (13.41) функції  функціями
функціями 
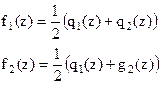
Використовуючи (13.38) і фільтруючу властивість дельта-функції, приведемо зазначену систему інтегральних рівнянь до наступного виду:
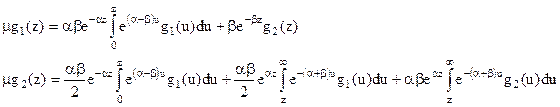 (13.46)
(13.46)
де  .
.
Після цілого ряду підстановок і перетворень знаходимо невідомі функції  :
:
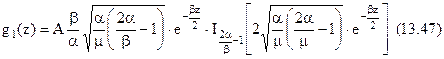
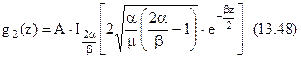
Підстановка (13.48) у (13.47) дозволяє визначити власні числа  :
:
Вираз для перших чотирьох кумулянтів розподілу процесу на виході фільтра:
Кумулянт першого порядку

Коефіцієнти асиметрії й ексцесу відповідно будуть рівні:
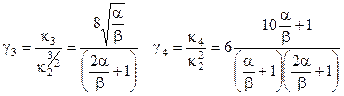
При великих 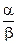 , тобто за умови, що смуга фільтра мала в порівнянні зі смугою ширини енергетичного спектра процесу на вході перемножувача, коефіцієнти асиметрії й ексцесу убувають як:
, тобто за умови, що смуга фільтра мала в порівнянні зі смугою ширини енергетичного спектра процесу на вході перемножувача, коефіцієнти асиметрії й ексцесу убувають як:
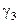 ~
~ ~
~
і прагнуть до нуля при  . Це говорить про нормалізацію процесу на виході типової ланки в міру відносного звуження ширини смуги пропуску вихідного фільтра.
. Це говорить про нормалізацію процесу на виході типової ланки в міру відносного звуження ширини смуги пропуску вихідного фільтра.
10.1. Ймовірнісні характеристики що обвідної і фази
10.1.1. Визначення обвідної і фази
При деяких припущеннях можна по заданому випадковому стаціонарному процесі 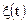 за допомогою перетворення Гільберта утворити новий, спряжений
за допомогою перетворення Гільберта утворити новий, спряжений 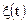 , стаціонарний випадковий процес
, стаціонарний випадковий процес

Збіжність (10.1) розуміється в середньоквадратичному смислі. Тоді випадковий процес 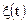 і спряжений йому можна представити у виді:
і спряжений йому можна представити у виді:
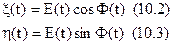
звідкіля випливає
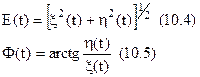
Визначені в такий спосіб випадкові процеси називаються
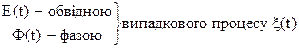 .
.
Помітимо, що з (10.4) випливає  тобто випадкова функція
тобто випадкова функція 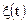 ніде не перетинає випадкову функцію
ніде не перетинає випадкову функцію  . І функція
. І функція 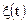 і
і  мають загальну дотичну в місцях зіткнення.
мають загальну дотичну в місцях зіткнення.
10.1.2. Представлення вузькосмугового процесу
Нехай  - деяка частота в смузі, де в основному зосереджений вузькосмуговий спектр випадкового процесу
- деяка частота в смузі, де в основному зосереджений вузькосмуговий спектр випадкового процесу 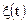 . Покладемо:
. Покладемо:
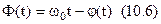
Підставляючи (10.6) у (10.2), одержуємо наступне представлення вузькосмугового випадкового процесу

Вводячи квадратурні складові
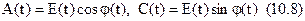
знаходимо

Аналогічно для сполученого процесу з (10.3) випливає

А з (10.7) випливає
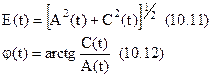
Тут обвідна  і фаза
і фаза 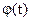 вузькосмугового випадкового процесу визначені, як нелінійні безінерційні перетворення квадратурних складових A(t), C(t) на відміну від співвідношень (10.4), (10.5), що визначають обвідну і фазу як нелінійні інерційні перетворення вихідного процесу
вузькосмугового випадкового процесу визначені, як нелінійні безінерційні перетворення квадратурних складових A(t), C(t) на відміну від співвідношень (10.4), (10.5), що визначають обвідну і фазу як нелінійні інерційні перетворення вихідного процесу 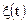 , так як спряжений процес
, так як спряжений процес  представляє реакцію лінійного фільтра на вхідний процес
представляє реакцію лінійного фільтра на вхідний процес 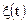 .
.
Іноді зручно буває записати вираз (10.7) як дійсну частину деякої комплексної величини

Z(t) – комплексна обвідна вузькосмугового процесу 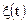 .
.
З (10.9) і (10.10) випливає
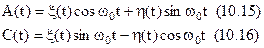
Приведені тут співвідношення вірні не тільки для вузькосмугових процесів.
10.1.4. Розподіл імовірності обвідної і фази
Для визначення багатомірної щільності імовірності обвідної E(t) і фази 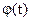 вузькосмугового процесу (10.18), скористаємося загальним методом.
вузькосмугового процесу (10.18), скористаємося загальним методом.
Нехай  - спільна щільність імовірності значень A(t) і C(t) у n моментах часу. Для того щоб знайти багатомірні щільності імовірності обвідної і фази, перейдемо відповідно до (10.20) і (10.21) у зазначеному спільному розподілі до полярних координат
- спільна щільність імовірності значень A(t) і C(t) у n моментах часу. Для того щоб знайти багатомірні щільності імовірності обвідної і фази, перейдемо відповідно до (10.20) і (10.21) у зазначеному спільному розподілі до полярних координат

де 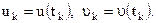
Після такої заміни замість сумісної щільності, що залежить від змінних  одержуємо 2n-мірну спільну щільність імовірності обвідної і фази, що залежать від змінних
одержуємо 2n-мірну спільну щільність імовірності обвідної і фази, що залежать від змінних 
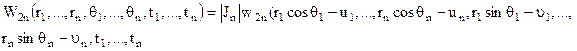 (10.23)
(10.23)
де
 (10.24)
(10.24)
- якобіан перетворення (10.22).
Підставимо (10.22) у (10.24), проведемо диференціювання й обчислимо детермінант

Багатомірна щільність імовірності обвідної виходить n-кратним інтегруванням (10.23) по змінним  :
:

У деяких задачах нелінійного перетворення обвідної розв’язання може бути отримане іноді швидше за допомогою характеристичної функції. Характеристична функція процесу 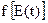 :
:

Для визначення енергетичних характеристик обвідної і фази слід спочатку попередньо по формулах (10.26) і (10.27) знайти їхній двовимірні щільності імовірності. А потім обчислити кореляційні функції і по теоремі Хінчина-Вінера спектральні щільності потужності.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 553; Нарушение авторских прав?; Мы поможем в написании вашей работы!