Лекція 7. 12.1. Нелінійні перетворення обвідної

12.1. Нелінійні перетворення обвідної

12.1.1. Функція розподілу квадрата обвідної

Визначимо двовимірну функцію розподілу 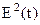, тобто квадрата обвідної вузькосмугового нормального випадкового процесу після квадратичного детектування.

Представимо вираз для двомірної функції розподілу, коли є присутнім детермінований сигнал:

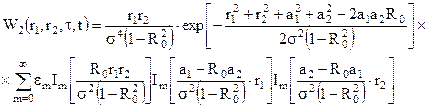(12.1)

де .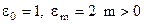

У виразі (12.1) перейдемо від змінних 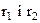до змінних:

, одержимо:

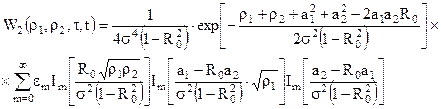(12.2)

Якщо сигнал відсутній, то 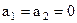, і

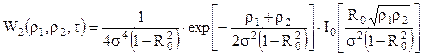(12.3)

Одномірну функцію розподілу неважко одержати, спрямувавши в (12.2)

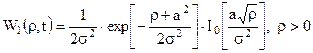(12.4)

При 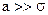функцію Бесселя можна замінити її асимптотичним наближенням:

~

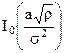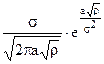
тоді

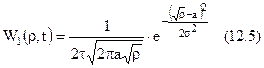
Коли сигнал відсутній, одномірна функція розподілу квадрата обвідної стаціонарного нормального гаусівського процесу дорівнює

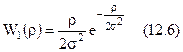
12.2. Кореляційна функція квадрата обвідної.

Визначимо кореляційну функцію квадрата обвідної стаціонарного нормального випадкового процесу, коли двомірна функція розподілу якого задана формулою (12.3), а одномірна (12.6).

Розкладання двомірної функції в ряд також здійснимо по поліномах Лагерра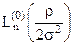

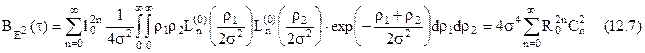
де .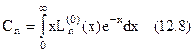

З огляду на властивості поліномів Лагерра, інтеграл (12.8) , для 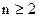, а коефіцієнти 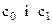будуть рівні:

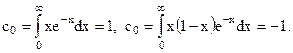
Так як

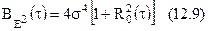
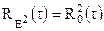- коефіцієнт кореляції квадрата що обгинає.

12.3. Ідеальне обмеження обвідної

Визначимо кореляційну функцію після ідеального (граничного) обмеження обвідної вузькосмугового стаціонарного нормального випадкового процесу. Нелінійне перетворення в ідеальному обмежувачі задається функцією:

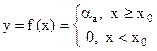
Для рішення поставленої задачі застосуємо прямий метод:

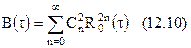
де

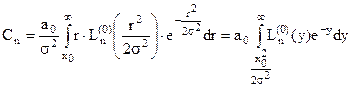
де 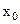- рівень обмеження.

Для n=0

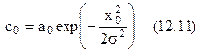
з огляду на визначення полінома Лагерра 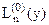, коефіцієнти 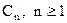, будуть рівні

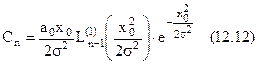
12.4. Логарифмічний детектор

Розглянемо логарифмічне перетворення обвідної

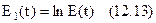
Знайдемо спочатку середнє і дисперсію логарифма обвідної нормального стаціонарного випадкового процесу з нульовим математичним сподіванням і дисперсією .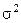

Так як одномірний розподіл E(t) у цьому випадку релеєвський, то

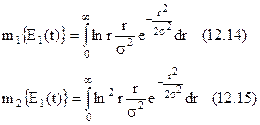
Заміною 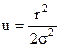інтеграли (12.14) і (12.15) приводяться до виду:

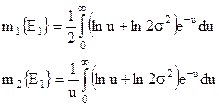
З врахуванням того, що

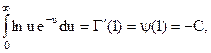
де 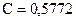- постійна Ейлера.

Одержимо:

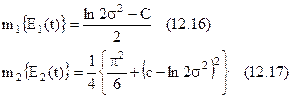
Дисперсія логарифма обвідної дорівнює:

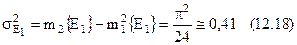
Кореляційна функція ln обвідної

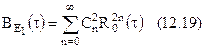
де

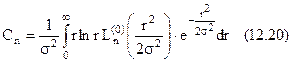
при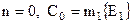

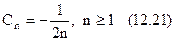
Остаточно одержуємо

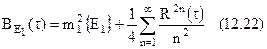
При 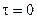(12.22) співпадає з (12.17), так як .

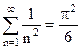Дата добавления: 2014-01-04