Визначення еквівалентного діаметра каналу в зернистому слою. Гідравлічний опір зернистого слою

Скористаємось рівнянням Гагена-Луазейля

(5.2.1)

Перепишемо рівняння (5.2.1) відносно 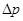, враховуючи, що по рівнянню витрати

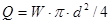
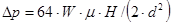(5.2.2)

Помноживши і розділивши праву частину виразу (5.2.2) на 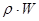, отримаємо

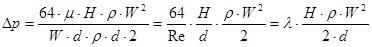
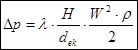(5.2.3)

В даному випадку коефіцієнт тертя 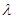відображає вплив не лише опору тертя, але і місцевих опорів. 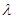є загальним коефіцієнтом опору, суттєво залежить від геометричних характеристик зернистого матеріалу і визначається по відповідним емпіричним рівнянням:

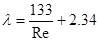(5.2.4)

Вирази для визначення часто є досить приблизними з причини полідисперсності зернистого матеріалу. Еквівалентний діаметр виражають через основні характеристики зернистого матеріалу - питому поверхню і вільний об’єм.

Під питомою поверхнею а (м²/м³) зернистого матеріалу або насадки розуміють поверхню частинок матеріалу, які знаходяться в одиниці об’єму, зайнятого цим матеріалом.

Долею вільного об’єму слою матеріалу (вільним об’ємом або пороpністю слою) 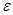називають відношення пустот між частинками до об’єму, зайнятому цим матеріалом. Якщо V - загальний об’єм, який займає зернистий слой, V_o - вільний об’єм слою, V_т - об’єм, який займають частинки, що утворюють слой, то

,

тобто величина 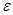- є безрозмірною і виражається в долях і відсотках. Позначивши густину матеріалу через 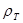, а насипну густину через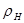, з урахуванням того, що

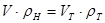отримаємо

,

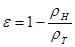При 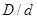<10 замітно проявляється так званий пристіночний ефект - збільшення порозності 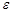біля стінки порівняно з 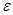в центральній частині апарату і, як наслідок, - до проскоку частини потоку без достатньо тривалого контакту зернистого слою. Таке явище називають боліпасуванням.

Еквівалентний діаметр зернистого слою в загальному вигляді можна записати, як

(5.2.5)

де S_к і П_к - відповідно площа перерізу і змочений периметр каналу, утвореного зернистим матеріалом або насадкою.

Величини Sк і Пк можна визначити наступним чином. Об’єм зернистого слоя в апараті , (де S - переріз апарату, заповненого зернистим слоєм на висоту Н). Тоді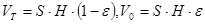, а поверхня частинок F, рівна поверхні утворюючих ними каналів, складає 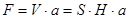(тобто в останньому випадку нехтуємо зменшенням поверхні частинок в результаті їх дотикання один з одним). Внаслідок хвилястості каналів їх довжина .

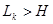Позначимо відношення 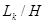як 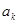. Це і буде коефіцієнт кривизни каналів, причому . Тоді вільний об’єм зернистого слою можна виразити як:

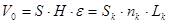. Звідси

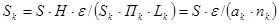(5.2.6)

де - число каналів в слою зернистого матеріалу насадки.

З урахуванням того, що 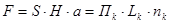величину П_к можна виразить наступним чином:

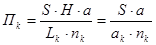(5.2.7)

Тоді еквівалентний діаметр каналів зернистого матеріалу:

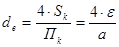(5.2.8)

Величину 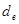можна виразити також розмір частинок слою зернистого матеріалу. Якщо в 1м³ слою зернистого матеріалу є n частинок об’ємом 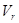і поверхнею 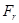кожна, то можна записати

,

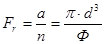де d – діаметр еквівалентного шару того ж об’єму, що і дана частинка;

Ф – коефіцієнт форми, який визначається за рівнянням , де 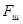- поверхня шару, який має тей же об’єм, що і дане тіло поверхнею F.

Для сферичних частинок Ф=1. Значення Ф для частинок різної форми приводиться в довідниках.

Тоді:

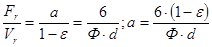(5.2.9)

Підставивши в рівняння (5.2.8) величину з рівняння (5.2.9), отримаємо новий вигляд рівняння для визначення еквівалентного діаметра каналу в зернистому слої.

(5.2.10)

В рівняння (5.2.3) входить величина w - швидкість рідини або газу в каналах слою зернистого матеріалу, котру складно знайти. Тому її виражають через так звану фиктивну швидкість W_о, під котрою розуміють швидкість, віднесену до всієї площі поперечного перерізу апарату, яку визначають з рівняння витрати.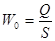. При усталеному режимі (де 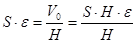- сумарна площа перерізу каналів). Звідси

(5.2.11)

Перепишемо рівняння (5.2.3) з урахуванням приведених вище залежностей.

Тоді після перетворення отримаємо

,

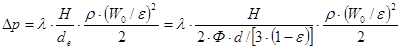або

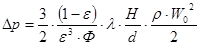, (5.2.12)

Коефіцієнт опору 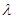є функцією гідродинамічного режиму руху потоку через слой зернистого матеріалу або насадки, тобто 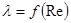. При цьому критерій Рейнольдса виражають в модифікованому вигляді, котрий отримують при підстановки в нього еквівалентного діаметра за рівнянням (5.2.10):

(5.2.13)

(5.2.14)

де - критерій Рейнольдса, виражений через швидкість W_о і діаметр d.

При русі рідини через слой зернистого матеріалу або насадки турбулентність розвивається при значно меньших, ніж при русі рідини по трубам, значеннях Rе, (так, ламінарний режим існує при Rе<50).

Для всіх режимів можна визначити 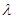по узагальненій залежності

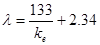, (5.2.15)

в котрій при малих значеннях Rе другим доданком можна знехтувати.

При Rе>7000 настає автомодельний турбулентний режим. При цьому коефіцієнт тертя не залежить від Rе і стає постійним: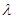=2,34.

Для руху рідини через дрібних частинок (що відповідає низьким значенням критерія Рейнольдса), підставимо в рівняння (5.2.12) значення 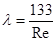, а Re – з рівняння (5.2.14), отримаємо новий вираз для визначення гідравлічного опору зернистого слою:

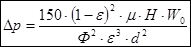(5.2.16)

котре називають рівнянням Козені - Кармона.

Дата добавления: 2014-01-04