Види функцій активації

Розглянемо основні види функцій активації, що одержали поширення в штучних НС.

1. Жорстка сходинка (мал..):

Використовується в класичному формальному нейроні. Розвито повну теорію [Мкртчян71], дозволяюща синтезувати довільні логічні схеми на основі ФН із такою нелінійністю. Функція обчислюється двома-трьома машинними інструкціями, тому нейрони з такою нелінійністю вимагають малих обчислювальних витрат.

Ця функція надмірно спрощена і не дозволяє моделювати схеми з безупинними сигналами. Відсутність першої похідної утрудняє застосування градієнтних методів для навчання таких нейронів. Мережі на класичних ФН найчастіше формуються, синтезуються, тобто їх параметри розраховуються по формулах, на противагу навчанню, коли параметри підбудовуються ітеративно.

2. Логічна функція (сигмоїда,функція Фермі, мал..):

Застосовується дуже часто для багатошарових перцептронов і інших мереж з безупинними сигналами. Гладкість, безперервність функції — важливі позитивні якості. Безперервність першої похідної дозволяє навчати мережа градієнтними методами (наприклад, метод зворотнього поширення помилки).

Функція симетрична щодо крапки (NET=0, OUT=1/2), це робить рівноправними значення OUT=0 і OUT=1, що істотно в роботі мережі. Проте, діапазон вихідних значень від 0 до 1 несиметричний, через це навчання значно сповільнюється.

Дана функція — стискаюча, тобто для малих значень NET коефіцієнт передачі K=OUT/NET великий, для великих значень він знижується. Тому діапазон сигналів, з якими нейрон працює без насичення, виявляється широким.

Значення похідної легко виражається через саму функцію. Швидкий розрахунок похідної прискорює навчання.

3. Гіперболічний тангенс (мал.):

Теж застосовується часто для мереж з безупинними сигналами. Функція симетрична відносно крапки (0,0), ця перевага в порівнянні із сигмоїдою.

Похідна також безупинна і виражається через саму функцію.

4. Положиста сходинка (мал.):

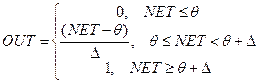
Розраховується легко, але має розривну першу похідну в крапках,

що ускладнює алгоритм навчання.

5. Експонента: . Застосовується в спеціальних випадках.

6. SOFTMAX-функція:

Тут підсумовування виробляється по всіх нейронах даного шару мережі. Такий вибір функції забезпечує суму виходів шаруючи, рівну одиниці при будь-яких значеннях сигналів даного шару. Це дозволяє трактувати 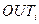як імовірності подій, сукупність яких (усі виходи шару) утворить повну групу. Ця корисна властивість дозволяє застосувати SOFTMAX-функцію в задачах класифікації, перевірки гіпотез, розпізнавання образів і у всіх інших, де вимагаються виходи-ймовірності.

7. Ділянки синусоїди:

8. Гаусова крива (мал.):

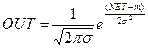
Застосовується у випадках, коли реакція нейрона повинна бути максимальною для деякого визначеного значення NET.

9. Лінійна функція, OUT = K NET, K =const.

Застосовується для тих моделей мереж, де не потрібне послідовне з'єднання шарів нейронів один за одним.

Тверда сходинка Сигмоїда(логічна крива) Гіперболічний тангенс

Сходинка з лінійною частиною Гаусова крива

Мал.. Види функцій активації.

Вибір функції активації визначається:

1. Специфікою задачі.

2. Зручністю реалізації на ЕОМ, у виді електричної чи схеми іншим способом.

3. Алгоритмом навчання: деякі алгоритми накладають обмеження на вид функції активації, їх потрібно враховувати.

Найчастіше вид нелінійності не робить принципового впливу на рішення задачі. Однак удалий вибір може скоротити час навчання в кілька раз.

Дата добавления: 2014-01-04