Прогнозування одномірної функції

Нехай задана функція визначена на інтервалі часу 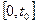, де 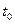— поточне значення часу. Потрібно пророчити значення функції при . Щоб застосувати багатошаровий перцептрон для прогнозування, час прийдеться дискретизувати. Будемо вважати відомими значення функції в моменти часу:

,

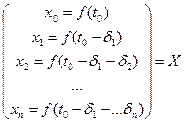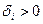
Будемо пророкувати значення функції в момент часу 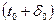для 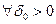. 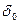називається інтервалом прогнозування. Рішенням задачі будемо вважати значення .

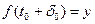Побудуємо мережу, що має n входів і 1 вихід. Як вхідний вектор візьмемо вектор x, а вихідного — один сигнал y.

Така мережа пророкує значення функції в одній крапці y по (n +1) відомих значеннях функції, заданим вектором x. Вибравши при навчанні мережі набір інтервалів 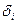, його не можна змінити після навчання. Мережа з даними параметрами , отриманими при навчанні, може прогнозувати тільки з одним набором .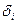

Чи можна прогнозувати функцію у виді дискретного процесу в часі? Як пророчити

кілька значень функції в різних крапках?

Для цього знайдений цікавий спосіб. Виберемо всі інтервали однаковими: 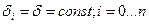Побудуємо і навчимо мережу. Подамо на вхід вектор x зі значеннями функції у відомих крапках. Розрахувавши вихід мережі, одержимо прогнозоване значення функції в крапці 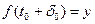. Тепер “зрушимо” компоненти вхідних і вихідних векторів у такий спосіб (знак рівності означає “привласнити значення”):

.

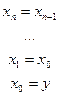
Тепер вихідний вектор став однієї з компонентів вхідного. Знову розраховуємо вихід, і одержуємо значення функції в крапці 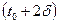. Повторивши ці операції, можна прогнозувати функцію у будь-якій кількості крапок з дискретним кроком за часом, рівним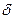

Дата добавления: 2014-01-04