Теорема Жуковського

Визначення зрівноважувальної сили методом М.Є.Жуковського. У випадку задач, у яких необхідно знайти зрівноважувальну силу або зрівноважувальний момент, а визначати реакції в кінематичних парах немає потреби, використовують теорему (метод) Жуковського. Прикладом таких задач є: визначення потужності та типу двигуна, моменту інерції маховика, характеристики регулятора та інші задачі динаміки.

Співвідношення між силами, прикладеними до ланок механізму (включаючи і сили інерції), можна дістати, застосувавши теорему Жуковського про жорсткий важіль: якщо для механізму, що перебуває в русі, побудувати план швидкостей, а потім вектори усіх активних сил та сил інерції, які прикладені в різних точках механізму, повернути на 90⁰ в один і той же бік та перенести в однойменні точки плану швидкостей, то сума моментів цих сил відносно полюса буде дорівнювати нулю.

Замість сил можна повертати план швидкостей на 90⁰, а сили прикладати так, як вони показані на схемі механізму. Тоді теорему Жуковського можна сформулювати таким чином: якщо до плану швидкостей, повернутого на 90⁰, у відповідних точках прикласти всі зовнішні сили (і моменти), сили інерції (і моменти сил інерції), а також зрівноважувальну силу (момент) і розглядати план швидкостей як жорсткий важіль, закріплений у полюсі, то під дією цих сил і моментів він буде перебувати в рівновазі, а сума моментів сил відносно полюса дорівнюватиме нулю. Таким чином, рівновазі механізму відповідає рівновага повернутого плану швидкостей, який розглядається як “жорсткий важіль”, що шарнірно закріплений в полюсі плану.

Доведення теореми ґрунтується на принципі можливих переміщень.

Моменти сил, що прикладені до ланок механізму найчастіше зображають у вигляді пар сил, які переносять на план швидкостей. Якщо моменти , що діють на ланки механізму, переносяться на план швидкостей безпосередньо у вигляді моментів, їх величина визначається рівнянням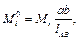

де 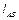, м – довжина ланки, до якої прикладений момент ; , мм – відрізок плану швидкостей, до якого прикладається момент. При цьому момент має той же знак, що і заданий момент , якщо напрям відрізка ab (порядок літер) співпадає з напрямом відрізка АВ схеми механізму. Якщо напрям ab протилежний АВ, то моменти та мають різні знаки.

Застосування важеля Жуковського дозволяє визначити шукану силу за допомогою тільки одного рівняння моментів. У випадку застосування методу плану сил необхідно провести повний силовий розрахунок механізму.

Відзначимо, що метод Жуковського можна застосовувати для знаходження величини будь-якої сили, якщо точка прикладання та лінія дії цієї сили задані, а також відомі лінії дії, величини та точки прикладання усіх інших сил, які діють на ланки механізму.

З наведеного випливає наступна послідовність визначення зрівноважувальної сили за способом Жуковського: - креслять кінематичну схему механізму у заданому положенні та вибраному масштабі з прикладеними усіма зовнішніми силами. Моменти замінюють парами сил; - будують план швидкостей, повернутий на 90⁰; - до однойменних точок повернутого плану прикладають усі зовнішні сили, сили інерції, а також зрівноважувальну силу, зберігаючи їх напрям; - складають рівняння суми моментів усіх сил відносно полюса і визначають зрівноважувальну силу.

Приклад. За допомогою важеля Жуковського визначити 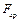для механізму, що зображений на рис. 3.11. Згідно з умовою 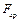прикладена в т. А кривошипа.

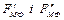У довільному масштабі будуємо план швидкостей. Прикладаємо у відповідних точках плану швидкостей всі сили, повернуті на 90⁰ за рухом стрілки годинника. При цьому моменти замінюємо парою сил , що прикладені в точках А та В, зі збереженням напрямку моменту

.

Складаємо рівняння моментів відносно полюса плану швидкостей ,

Звідки .

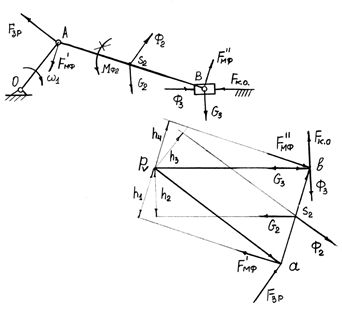
Рис. 3.11

Якщо при розв’язку даного рівняння сила додатня, то це означає, що її напрям вибрано правильно. При від’ємному значенні правої частини напрям сили треба змінити на протилежний.

Питання для самоконтролю

1. Що вивчає динаміка?
2. Сформулюйте основні задачі динаміки.
3. Назвіть сили, що діють на ланки механізму, та дайте їм коротку характеристику.
4. Дати означення механічної характеристики машини.
5. На якому принципі теоретичної механіки ґрунтується кінетостатичний розрахунок механізму?
6. Яка послідовність силового розрахунку механізмів?
7. Яка умова статичної визначеності кінематичних ланцюгів?
8. Сформулюйте теорему Жуковського.

ГЛАВА 4. ДОСЛІДЖЕННЯ РУХУ МАШИННОГО АГРЕГАТУ

Вивчення закону руху механізму машинного агрегату під дією заданих сил є однією з основних задач динаміки. Для розв’язку цієї задачі необхідно скласти рівняння руху системи і розв’язати його відносно невідомого кінематичного параметра. При визначенні закону руху задача може бути суттєво спрощена, якщо перейти до динамічної моделі.

Вивчення динаміки машини повинно починатися з вибору її динамічної моделі. Вибір динамічної моделі того чи іншого об’єкта залежить, у першу чергу, від мети дослідження, від характеру задачі, що розглядається.

Дата добавления: 2014-01-04